形式语言与自动机复习笔记
绪论(一)
1.语言
语言L是句子的集合,当含有穷个句子时L为有穷语言,含无穷可数个句子时L为无穷语言;
E是一个字母表,L包含于E的【克林闭包】,则称L是E上的一个语言;

语言的特殊运算法则: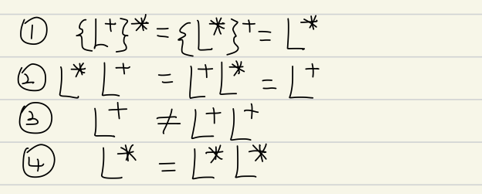
2.文法

正则语言(二)
1.有穷自动机FA

1.1 *DFA
确定有穷状态自动机DFA

要求构造识别某个语言的DFA时,按照上述的步骤进行即可,非常简单;
需要注意一个定理
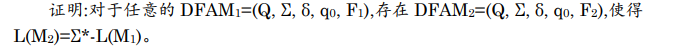
该定理只能用于DFA(不能直接用于NFA),可以帮助我们非常方便的构造某个语言的反例,只需要将原本DFA的终止状态和非终止状态互换即可(注意是否包含空串),如
这是识别语言{x不含空串且x含10110的子串}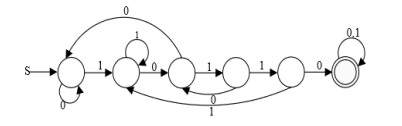
这是识别语言{x不含空串且x不含10110的子串}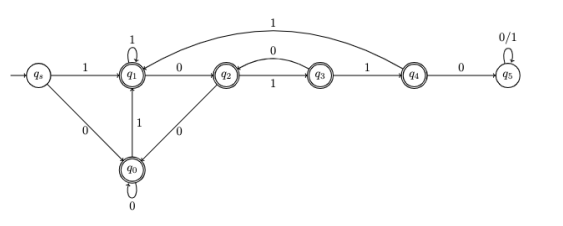
1.2 *NFA
非确定有穷状态自动机NFA

当要求构造能够识别语言的NFA时,通常其做法比DFA简单的多(除了待会要说的例外),只需要分析需要几种状态并直接顺着弧线往下写就行,多写弧线并不会扣分;
1.2.1 *NFA->DFA

注意:
- 正确快速的做题方法是,在写DFA的时候,比如{q0,q1}读入0,则盯住NFA中的0对应的列,直接寻找q0的行和q1的行求并集即可;
- 开始状态只能有q0一个,但是终止状态只要含原NFA终止状态则算终止状态;
1.3 s-NFA
带空移动的非确定有穷状态自动机s-NFA

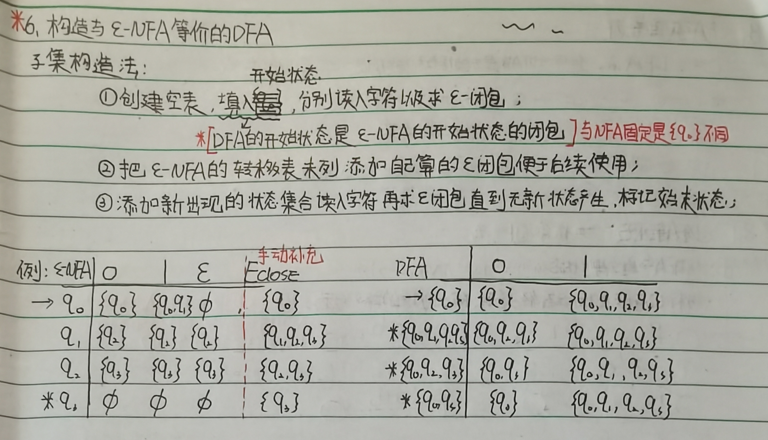
1.3.1 *s-NFA->DFA
注意:
书上的方法太容易混淆了,这里我们就使用此处介绍的方法即可;
一定要标记始末状态,DFA的初始状态为s-NFA初始状态的闭包,DFA的终止状态为包含s-NFA的终止状态的状态集合;
关于DFA的初始状态怎么求,一定要注意是s-NFA的初始状态的闭包;
某个状态qi的闭包的求法是包括自身,经过任意步数的空移动能够到达的【全部】状态的集合;
关于DFA的格子,并不是简单的读入字符移动到某个状态集合(如{q0,q1}),而是移动到的状态集合的s-闭包(如{q0,q1,q2,q3});
1.4 FA与RG
1.4.1 FA->RG
这里我们使用右线性文法举例,右线性文法的定义是,产生式集P中的产生式形如 A->w , A->wB;
考点是给出FA(一般是状态转移图形式),构造所给的DFA对应的右线性文法;
基本步骤:
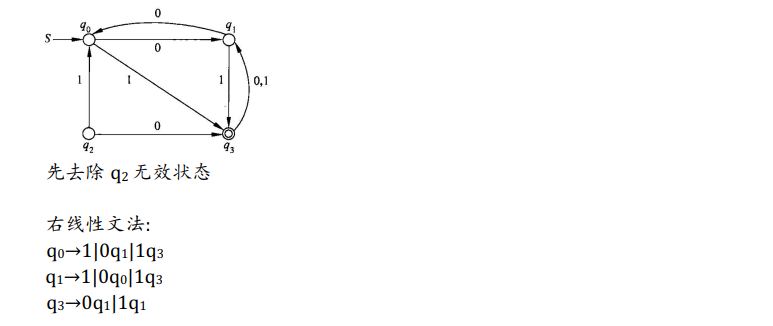
(1)预处理,先去除不可达状态和陷阱状态;
(2)使用变量一一对应状态(当然这一步完全可以省略,便于直接读图写产生式),如S对应q0起始状态、A对应q1状态、B对应q2状态;
(3)文法的产生式与状态转移函数一一对应,通过读图知道状态转移函数进而写出文法产生式;
需要注意的是,每个变量的产生式只根据其出边的状态转移函数构造,且若下一个状态是终止状态,则可以产生终极符号|终极符号 终止状态;
1.4.2 RG->FA
这里常见的考题将左线性或右线性文法转换为FA都有,我们常使用状态转移图来表示得到的FA;
解题方法使用构图法:
(1)在原有变量的基础上需要额外增加一个终止状态变量Z;
(2)通过文法产生式与状态转移函数的一一对应,可以直接根据文法作图;
注意:
- 这里文法产生式中如果有单独的终极符出现,说明这个状态读入该终极符后会转移到终止状态;
- 假如是让我们将左线性文法转换为FA,左线性文法的start箭头指向终止状态Z,先看产生式右边,S->Aa表示A读入a转移到S,S->a表示Z(终止状态)读入a转移到S;
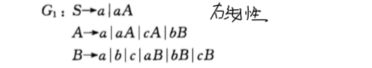
这里展示将右线性文法转换为FA
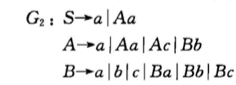
这里展示将左线性文法转换为FA
1.5 带输出的FA
1.5.1 Moore机

1.5.2 Mealy机

Moore机处理一个字符串时每经过一个状态,输出一个字符——输出的字符和状态一一对应;
Mealy机处理一个字符串时每一个移动输出一个字符——输出字符和移动一一对应;
2.RE

FA与RE等价
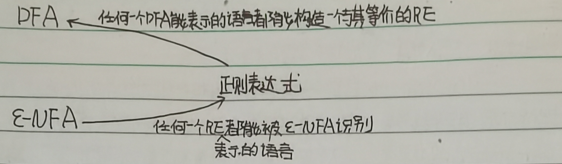
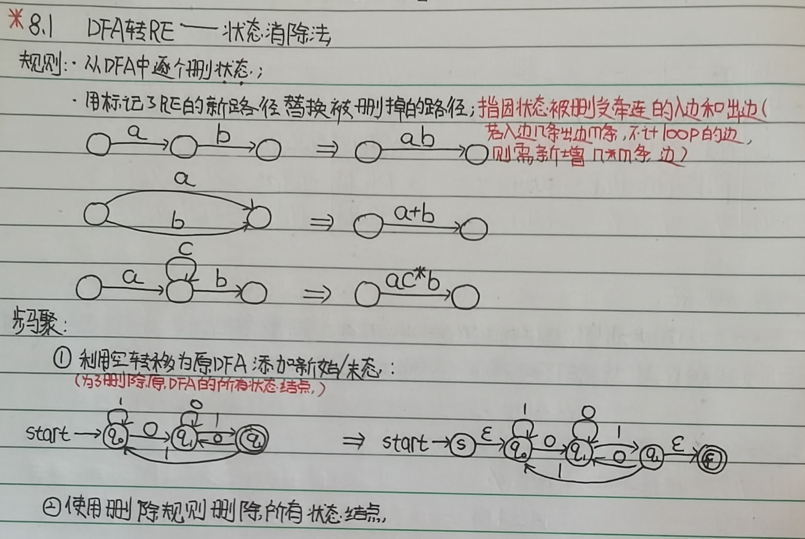
2.1 *DFA->RE
下面这两种类型的题都需要参考哈工大的解法,如果参照书本或者之前的解法,考试的时候根本没办法画的出来;
2.2 *RE->s-NFA
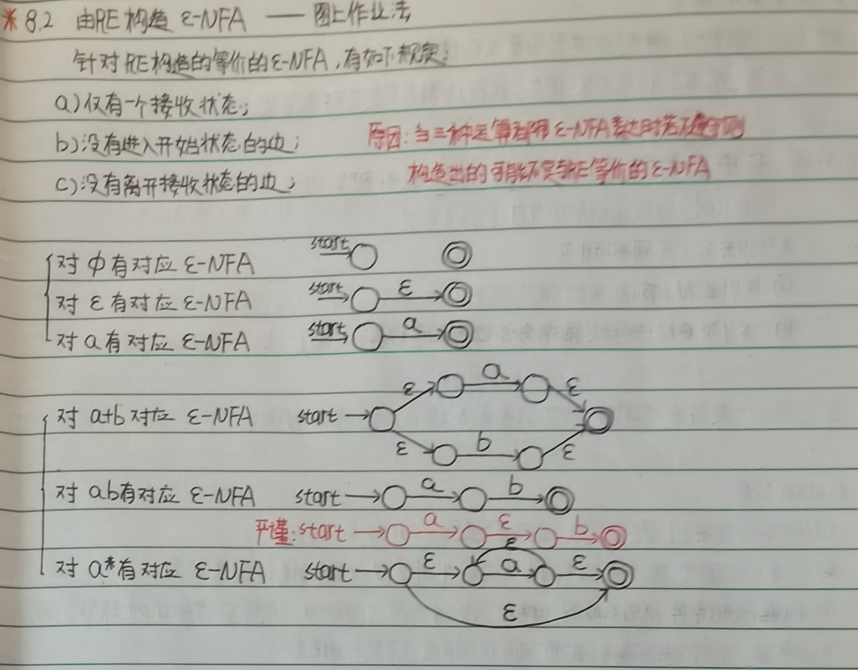
从左到右,按照运算时的优先级画图构造;
3.正则语言的性质
3.1 正则语言的泵引理

有关泵引理需要补充几点:
- 首先笔记中仅根据限制条件给出了w和y的表达式,在做题时确实只需要这两个即可,不要考虑过多导致思路不清晰;
- 我们在分类讨论的时候只需要设【下限】即可,不要考虑过多的因素导致思路不清晰;
- 当y^2不好用时尝试用y^0;

3.2 正则语言的封闭性

3.3 *DFA的最小化

关于上面的填表算法,需要补充:
- 在第一步之前我们还需要删去不可达状态(陷阱状态要保留);
- 创建空表,形式如下
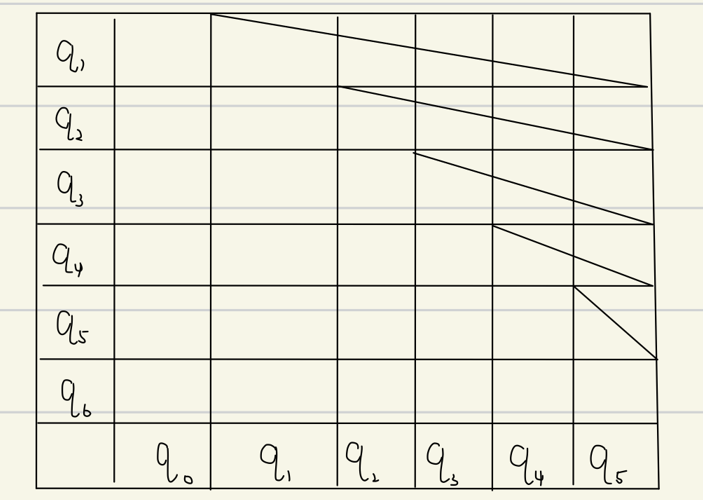
- 先根据接受状态和不接受状态一定可区分,在空表中做标记;
- 接着对未标记的状态对从上往下,从左往右依次读入字母表上的字符0/1(字母表中的字符都需要读!!)
- 只要转移到的状态对有一个是做了标记的,则该状态对也需要做标记;
- 假如转移到的状态对是形如[q0,q0]这种或者还未知是否需要做标记的,则该状态对待定;
- 假如转移到的状态对全是形如[q0,q0],[q1,q1]这种,则可以确定该状态对一定不能做标记(也就是该状态对一定等价);
- 将空格读完即可,不要使用那种根据状态对反向推导的方法,很容易出问题;
上下文无关语言(三)
1.基本概念
1.1 上下文无关文法CFG的定义

1.2 上下文无关语言CFL的定义
若CFG G,则G的语言指的是从初始符号推导出的所有终结符的串的集合;
1.3 语法分析树

关于语法分析树,也称派生树,书上的介绍很少,但是作业题中出现了相关的考点:
(1)根据已知语法分析树给出其结果的最左派生(推导也称为派生):这种题做法就是直接顺着根节点往下,逐步利用产生式替换最左边出现的变量
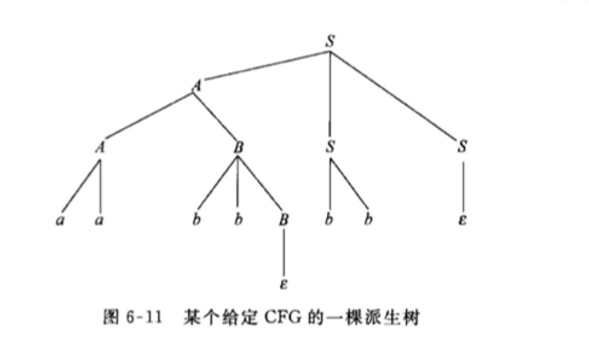
该语法树对应的最左派生为
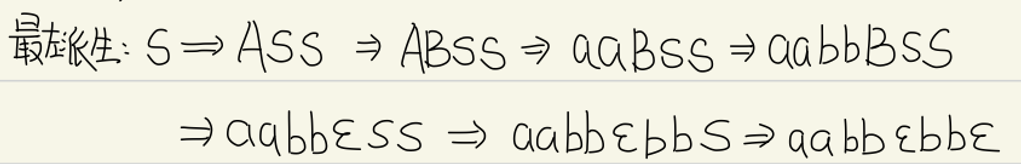
(2)第二种考点是写出派生树有多少种不同派生,关键在于排列组合

(3)第三种考点是根据派生树写出相应的CFG,做法就是直接读图写变量的产生式即可(树上有什么就写什么,空串也要写,但是派生树终极结果可以忽略空串)
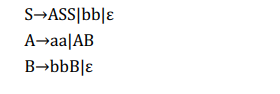
2.*CFG的化简

2.1 删除无用符号

2.2 删除空产生式

删除空产生式是删除自己的空产生式,弥补别人;
删除单一产生式是删除自己的单一产生式,弥补自己;
2.3 删除单一产生式

注意:关于删除单一产生式,只有A->w这种才不算单一产生式,形如B->B或者A->B或者S->A这种都是单一产生式,必须全部删除(对于B->B这种直接在原产生式中删除即可)
3.乔姆斯基范式CNF
3.1 CNF定义

3.2 *CFG->CNF

注意:
这里尤其要注意一点,考题可能会给出一个未化简的式子,所以假如未化简我们需要使用上面的 删除无用符号-去除空产生式-去除单一产生式-删除无用符号 的步骤进行化简;
其次是注意,对【句型aAdB】中的终极符需要构建产生式替代,如果产生式右边是【句子abcd】也需要进行替换,将所有产生式处理为产生式右边【全是】变量符号ABCD或者【只有一个】终极符a;
最后是引入的符号最好可以区分,比如第一次处理引入的符号为C D,则第二次引入的符号应该是B1 B2
4.格雷巴赫范式GNF
4.1 GNF定义

4.2 *CFG->GNF

注意点:
- 第一步是检查上下文无关文法是否为最简;
- 第二步是将【原有变量】全部替换为带下标的A1 A2 A3;
- 第三步是引入额外变量C D对终极符替换,使得所有的产生式右部的第二个符号到最后一个符号都是变量,或者是产生式右部只有一个终结符;
- 第四步是调整原有变量下标顺序,消除间接左递归;
- 第五步是构造产生式组消除直接左递归;
- 最后一步就是将符合GNF定义的产生式比如A3的产生式全部代入还未符合GNF的变量如A2中
5.下推自动机PDA
5.1 PDA定义

5.2 PDA Pn->PDA Pf

本质上就是在Pf露出栈顶X0的时候(也就是Pn栈空了),直接转移到Pf的接收状态,因为对所有的Pn的状态都有可能被终态接受,所以为每一个状态添加转移;
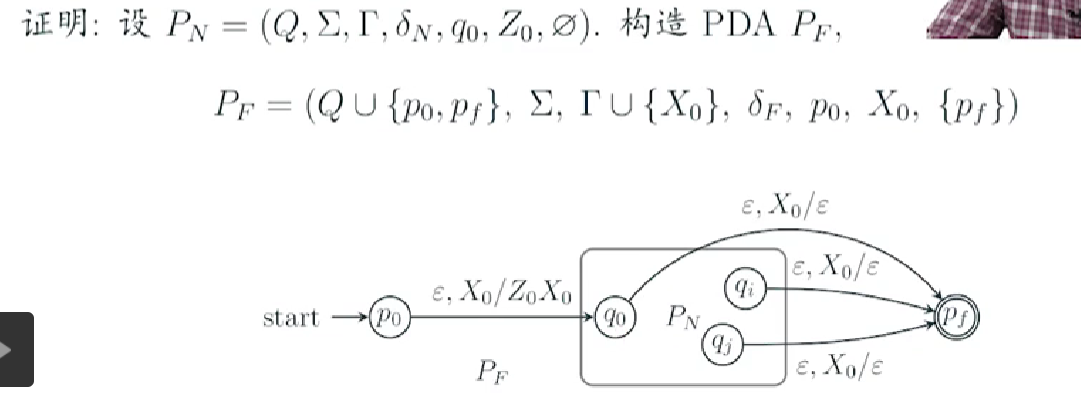
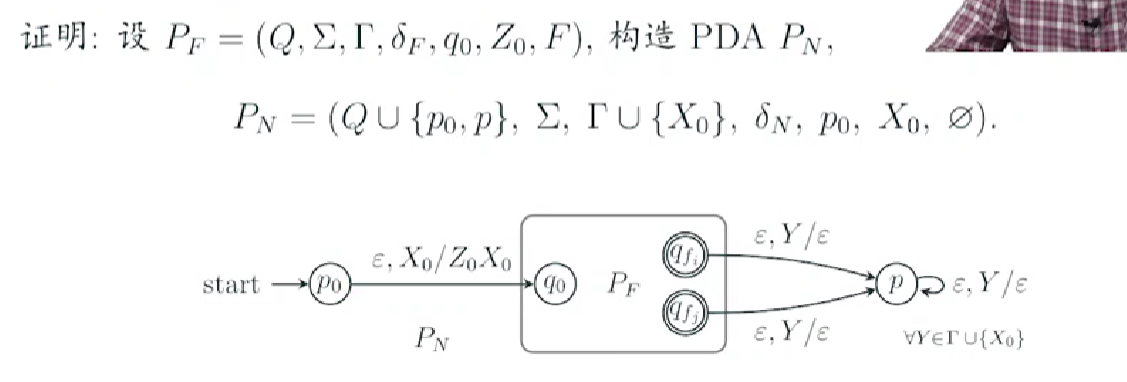
5.3 PDA Pf->PDA Pn

本质上就是在Pf的接收状态时,给Pf的接收状态补充一个弹栈的操作,可以直接清栈,但是给每个接收状态都这样做比较麻烦,所以干脆直接将所有接收状态空转移到新的终态P再清栈;
5.4 *CFG->PDA Pn

尽管说是任何CFG可以转换为PDA,但注意我们还是应该对CFG进行化简后再使用;
5.5 GNF->PDA Pn
当CFG是GNF的时候我们有一种更简单的转换方法(当然简单的CFG我们就没必要再花费时间转换为GNF再转换为PDA)

下面来看两道例题,区分CFG和GNF转换为PDA Pn的不同

5.5 *PDA Pn->CFG

下面给出一道例题便于理解

6.CFL的性质
6.1 *CFL的泵引理

注意:
- 不要在意所给的语言是多么复杂,我们只需要找到其中的一个符合该语言特征的句子即可;
- 对于CFL的泵引理来说常用的就是v^0和x^0;
- 假如泵出来是正确的说明我们找的句子z没找对,重新再找一个即可;
- 注意让我们判断句子是否是CFL或者RL基本上都不是,不要自认为可以证明出来它是;
6.2 CFL的封闭性

6.3 CFL的判定性质

短语结构语言(四)
1.图灵机TM
1.1 TM概念

1.2 TM的状态转移图

1.3 TM的状态转移表

1.4 TM的瞬时描述ID

1.5 TM接受的语言

1.6 TM的变形

1.7 非确定图灵机NTM

上下文有关语言(五)
上一章介绍的图灵机与短语结构文法是等价的,这里不再给出证明;
本章主要介绍识别上下文有关语言CLS的工具——线性有界自动机LBA;
1.线性有界自动机
LBA是一种非确定的图灵机:
- 输入字母表中包含两个特殊字符,C作为输入符号串的左端标志,S作为输入符号串的右端标志;
- LBA的读头只能在C和S之间移动,且LBA不能在端点符号C和S上打印另外的符号
