神经网络与深度学习
2022/9/11 10:51 还是得说一下,这门课程属于专业课,可能对数学要求真的比较高,所以自己看书啥的感觉真的不是一般人能够看的下去的,这里还是比较推荐直接对着相应的章节啃B站讲解视频,至少现在为止是真的没有发现一本能够将我讲明白的这类的书籍;
绪论
Q1:深度学习和神经网络是什么关系?各有什么相同点和不同点?
A:深度学习与神经网络既有交集也有各自的集合,深度学习如深度森林不属于神经网络,单层神经网络不属于深度学习
绪论其实也讲不了啥,相应的前置知识点我之前的博客应该也介绍过,然后我就简单针对这门课程做一个说明,首先是本学期的课程内容:
- 全连接神经网络
- 卷积神经网络
- 网络优化与正则化
- 循环神经网络
- 注意力机制
- 自编码器与表示学习
- 图神经网络
- 生成模型(VAE&GAN)
- 强化学习
然后因为这门课程其实不需要最终的期末考试…所以也就是注重平时作业的完成度即可;
第一章 全连接神经网络
文章参考:全连接神经网络(DNN) - 凌逆战 - 博客园 (cnblogs.com)
全连接神经网络也被称为多层感知机MLP、深度神经网络DNN,是一种连接方式较为简单的人工神经网络,属于前馈神经网络的一种;
1.网络结构
DNN的网络结构不是固定的,一般包含一个输入层、隐藏层以及一个输出层,每一层神经网络有若干神经元,层与层之间神经元相互连接,层内神经元互不连接,而且下一层神经元连接上一层所有的神经元。
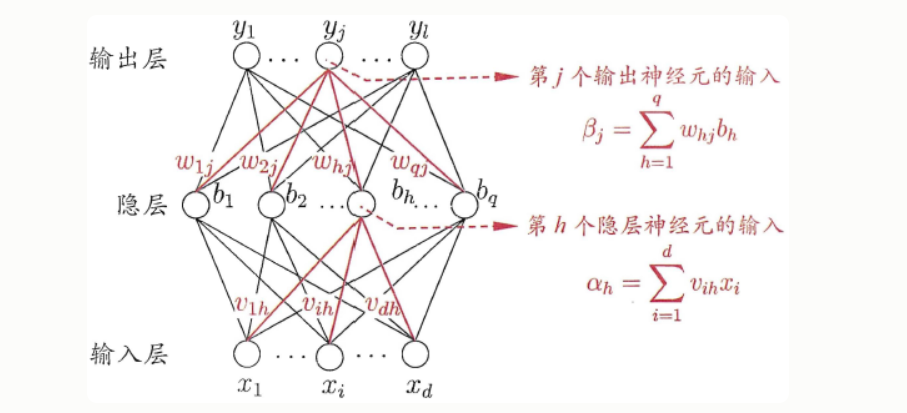
DNN的优点在于几乎可以拟合任何函数,其非线性拟合能力非常强;缺点在于DNN不容易训练,需要大量数据以及较多技巧才能训练好一个深层网络;
有关全连接神经网络的介绍我们在机器学习 - Tintoki_blog (gintoki-jpg.github.io)中写的很详细,这里就不再赘述;
第二章 卷积神经网络
文章参考:
视频参考:
卷积神经网络是一类强大的、为处理图像数据专门设计的神经网络;
卷积神经网络需要的参数少于全连接架构的网络,而且卷积也很容易用GPU并行计算。因此卷积神经网络除了能够高效地采样从而获得精确的模型,还能够高效地计算;
卷积神经网络将空间不变性(无论哪种方法找到目标物体,都应该和物体的位置无关)这一概念系统化,从而基于该模型使用较少的参数来学习有用的表示;同时在设计适合于计算机视觉的神经网络架构时需要考虑以下两点原则:
- 平移不变性(translation invariance):不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。
- 局部性(locality):神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
1.卷积神经网络和传统网络
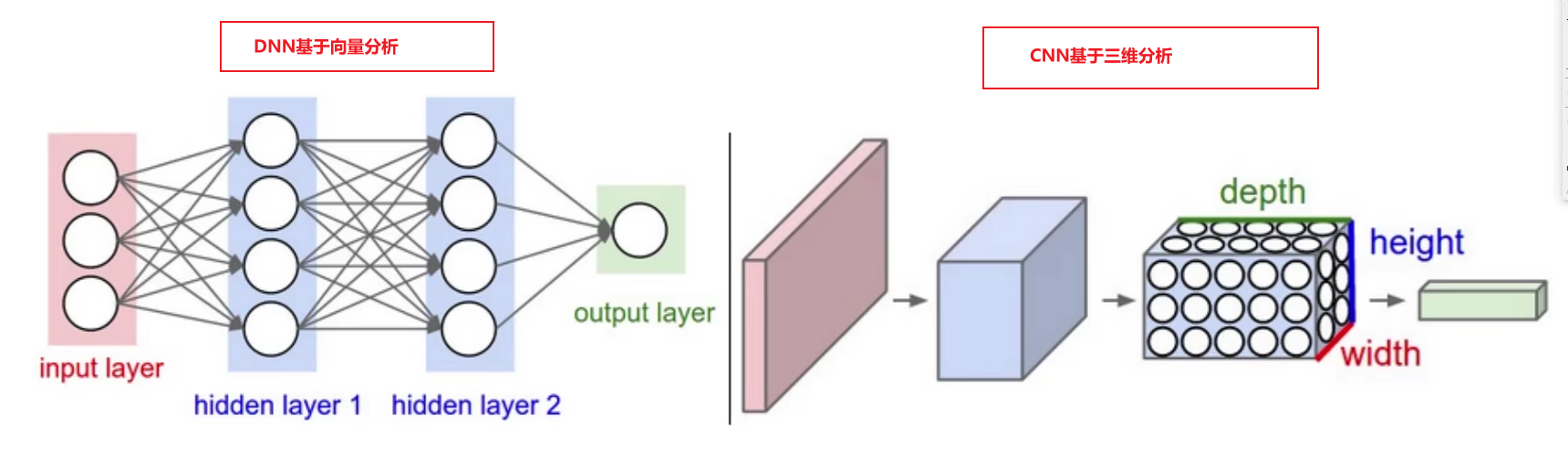
卷积神经网络基本层次结构为:
- 输入层:输入为三维28x28x1的数据;
- 卷积层
- 池化层
- 全连接层:全连接神经网络有介绍;
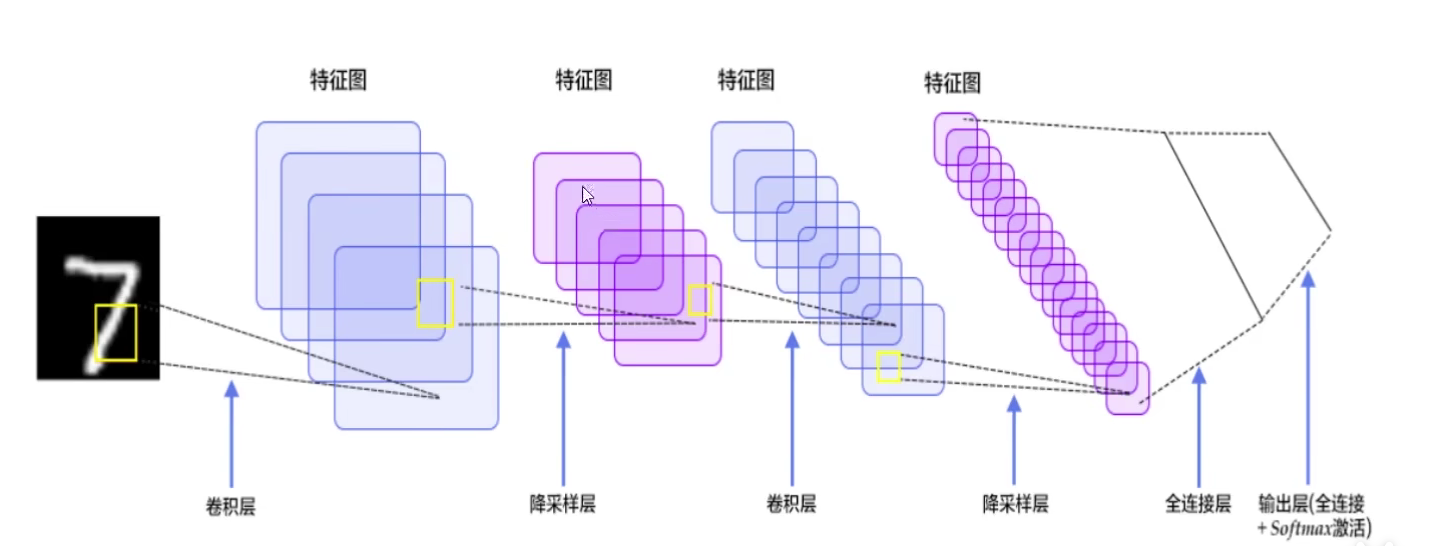
2.卷积层
卷积是进行特征提取的一种方式,卷积神经网络中同样是使用一组权重参数得到特征值
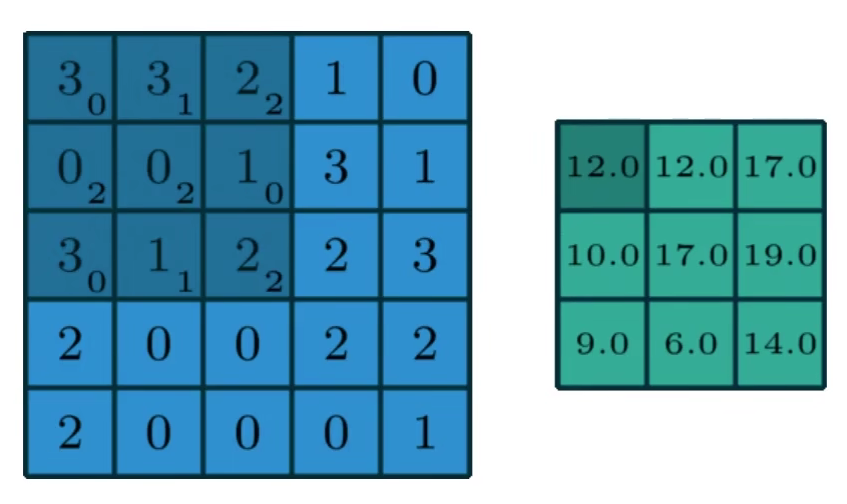
假设上图左边是我们的一个灰度图(5x5x1),现在我们取3x3x1的区域用作卷积提取特征
$$
[[3,3,2],[0,0,1],[3,1,2]]*[[0,1,2],[2,2,0],[0,1,2]]
$$
前者是像素矩阵,后者是权重参数矩阵,我们经过一次卷积过后得到右边的特征图;
我们知道彩色图像是nxnx3的,其中3代表有三个颜色通道RGB channel,在做卷积的时候每个颜色通道需要分别去做计算,将每个通道的计算结果相加得到最后的卷积结果;
下面我们给出一个直观的计算图,注意此处使用的矩阵乘法是矩阵内积(结果是标量,实际就是对应数据相乘相加,不同于矩阵外积的结果是一个矩阵)
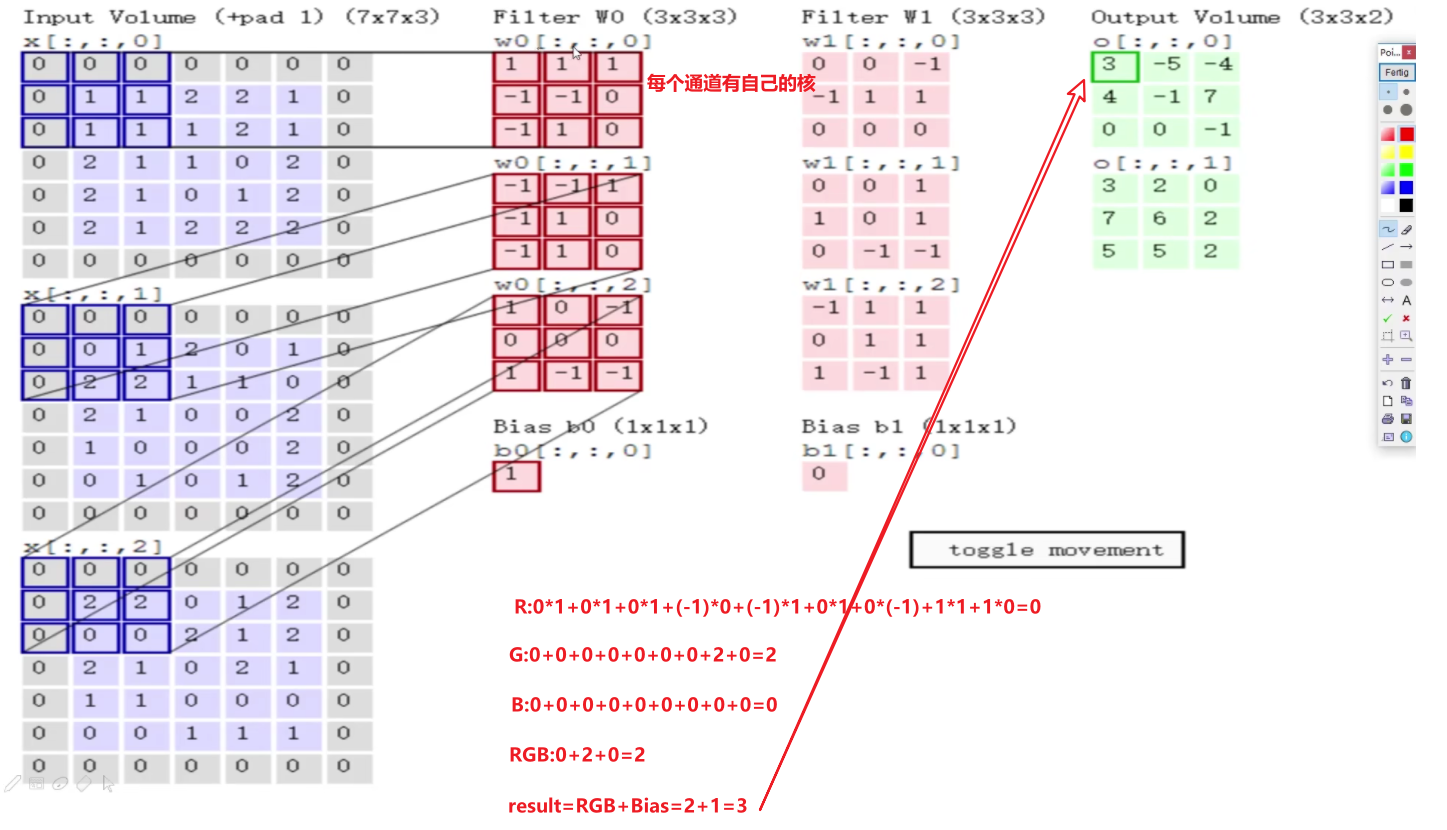
上面之所以输出的是两个特征图,是因为我们使用了两个卷积核来提取特征
Q:同一个卷积核,其权重参数矩阵能不能改变呢?
A:注意一点卷积核也被称为权重参数矩阵,这是两个等价的概念,同一个卷积核是不能变的,不能说在移动的过程中改变其中某个矩阵参数;
为什么不能?因为如果对于不同的区域使用不同的权重参数矩阵,这将导致所需的参数量变得非常大(而我们之所以选择CNN而不是DNN就是看重它的参数较少的特点);
卷积核不能修改的这个特性被称为卷积参数共享;
卷积层涉及概念:
- 假设输入的是一个7 * 7的二维神经元,我们定义3 * 3的一个
感受视野,也就是隐藏层的神经元与输入层的3 * 3个神经元相连,可以类似看作隐藏层中的神经元具有一个固定大小的感受视野去感受上一层的部分特征,全连接神经网络中的隐藏层的神经元的感受视野足够大以至于可以看到上一层的所有特征,但是在卷积神经网络中隐藏层中的神经元的感受视野比较小,只能看到上一层的部分特征,上一层的其他特征可以通过平移感受视野来得到同一层的其他神经元; - 将感受视野中的权重矩阵称为
卷积核; - 将感受视野中对输入的扫描间隔称为
步长; - 将通过带有卷积核的感受视野扫描生成的下一层神经元矩阵称为一个
特征映射图—— 在一个特征映射图上的神经元使用的卷积核是相同的,这些神经元共享卷积核中的权值和偏移; - 边缘填充:越往边界的点被利用的次数越少,越往中间的点被利用的次数越多,但是这就不公平了,我们的初衷是给的5 * 5的图像中的每个点都重要,那就使用边缘填充使其成为7 * 7的图像以弥补一些边缘信息缺失的问题(注意边缘填充的值最好用0,否则会导致最终结果受到影响)
3.池化层
在实际的训练中,我们并不需要对图像中的每一个细节都进行特征提取和训练,所以池化的作用就是更进一步的信息抽象和特征提取,当然也会减小数据的处理量;因此当得到的特征图比较大的时候,可以通过池化层对每一个特征图进行降维操作(实际上是压缩操作,但是特征图的数量也就是深度仍然不变);
池化层有一个池化视野来对特征图矩阵进行扫描,池化视野中的矩阵值计算一般有两种计算方式:
- 最大池化:取池化视野矩阵中的最大值(值越大的代表这个值越重要,这个特征越好);
- 平均池化:取池化视野矩阵中的平均值
总结池化层的优点:
池化层优点有:
- 不变性,更关注是否存在某些特征而不是特征具体的位置。可以看作加了一个很强的先验,让学到的特征要能容忍一些的变化。(实际上这个容忍能力是非常有限的)
- 减少下一层输入大小,减少计算量和参数量。
- 获得定长输出。(文本分类的时候输入是不定长的,可以通过池化获得定长输出)
- 防止过拟合或有可能会带来欠拟合。
4.卷积神经网络的网络架构
CNN由输入层、输出层以及多个隐藏层组成,隐藏层可分为卷积层、池化层、RELU层以及全连接层:
- 输入层:CNN的输入为原始图像,三维(RGB)或二维的向量。
- 卷积层:CNN的核心,卷积层由一组可学习的滤波器(filter)或内核(kernels)组成,它们具有小的感受野,每个卷积核具有kernel size,padding,stride等参数。从图像的左上角依次做内积操作,提取出图片的高层次特征。
- 池化层:对conv后输出的feature map进行下采样操作,这样的好处有降低参数的数量,防止过拟合等作用。
- 激活层:在CNN中使用relu激活函数,在网络中引入了非线性(卷积操作是把输入图像和卷积核进行相应的线性变换,需要引入激活层非线性函数对其进行非线性映射)。通过relu激活函数传递卷积运算的结果。因此,最终特征映射中的值不是简单的线性关系。
- 全连接层:将输入的特征图转化成一维的一个向量(简单的说就是将特征表示整合成一个值,起到分类器的作用,具体实现就是把特征图拉长之后进行全连接计算),由此实现了端到端的学习过程(即:输入一张图像或一段语音,输出一个向量或信息)
- 输出层:用于输出结果;
除了上述必要的层次以外,还可以增加一些功能层:
- 归一化层(Batch Normalization):在CNN中对特征的归一化
- 切分层:对某些(图片)数据的进行分区域的单独学习
- 融合层:对独立进行特征学习的分支进行融合
网络层数的定义:只有附带未知参数计算的层才能算数层数中,激活层和池化层不能计入网络层数
说明:深度学习这篇博客写不下去了…一方面难度比较大纯学习理论知识不容易掌握,另一方面前面讲机器学习的时候其实也多少涉及了深度学习相关的大部分核心内容。之后我就不会再更新这篇博客了,感兴趣可以看我其他专业课项目相关的博客,那里面会结合实际的项目对常见的深度学习网络进行介绍。