Tensorflow

第一章 tensorflow2.x基础

1.数据类型

tensorflow内部的数据均保存在张量对象上，所有的OP都是基于张量对象进行的；tensorflow中的基本数据类型包含数值类型、字符串类型和布尔类型；

1.1 数值类型

数值类型的张量是tensorflow主要的数据载体，根据维度可以分为：

  • 标量（Scalar）：单个的实数，如1.2，3.4等，维度（Dimension）数为0，shape为[]；

  • 向量（Vector）：n个实数的有序集合，通过中括号包裹，如[1.2]，[1.2，3.4]等，维度数为1，长度不定，shape为[n]；

  • 矩阵（Matrix）：n行m列实数的有序集合，如[[1，2]，[3，4]]，维度为2，每个维度上的长度不定，shape为[n,m]；

  • 张量（Tensor）：所有维度数dim >2的数组统称为张量。张量的每个维度也称作轴（Axis），每个维度代表了具体的物理含义。比如Shape为[2，32，32，3]的张量共有4维，如果表示图片数据的话，每个维度/轴代表的含义分别是图片数量、图片高度、图片宽度、图片通道数，其中2代表了2张图片，32代表了高、宽均为32，3代表了RGB共3个通道。张量的维度数以及每个维度所代表的具体物理含义需要由用户自行定义；

tensorflow中将上述四者统称为张量，可以根据张量的维度或形状自行判断；

创建0维张量

1
2
3
4
5
6
In [1]:
	a = 1.2 # python 语言方式创建标量
	aa = tf.constant(1.2) # TF 方式创建标量
	type(a), type(aa), tf.is_tensor(aa)#输出类型以及判断是否为tensor
Out[1]:
	(float, tensorflow.python.framework.ops.EagerTensor, True)

与标量不同，向量的定义须通过 List 容器传给 tf.constant()函数

创建向量

1
2
3
4
5
In [5]:
	a = tf.constant([1,2, 3.]) # 创建 3 个元素的向量
	a, a.shape
Out[5]:
	(<tf.Tensor: id=11, shape=(3,), dtype=float32, numpy=array([1., 2., 3.],dtype=float32)>,TensorShape([3]))

创建矩阵

1
2
3
4
5
In [6]:
	a = tf.constant([[1,2],[3,4]]) # 创建 2 行 2 列的矩阵
	a, a.shape
Out[6]:
	(<tf.Tensor: id=13, shape=(2, 2), dtype=int32, numpy=array([[1, 2],[3, 4]])>, TensorShape([2, 2])

1.1.1 数值精度

对于数值类型的张量，可以保存为不同字节长度的精度，位越长则精度越高占用的内存空间越大；

常用的精度类型有tf.int16、tf.int32、tf.int64、tf.float16、tf.float32、tf.float64 等，其中 tf.float64 即为 tf.double；

在创建张量的同时可以指定张量的保存精度

1
2
3
4
5
6
In [12]: # 创建指定精度的张量
tf.constant(123456789, dtype=tf.int16)
tf.constant(123456789, dtype=tf.int32)
Out[12]:
<tf.Tensor: id=33, shape=(), dtype=int16, numpy=-13035>#保存精度过低，数据发生溢出（一般不选择int16保存精度)
<tf.Tensor: id=35, shape=(), dtype=int32, numpy=123456789>

通过访问张量的dtype成员属性可以判断张量的保存精度

1
2
3
4
5
6
7
8
9
In [15]:
print('before:',a.dtype) # 读取原有张量的数值精度
if a.dtype != tf.float32: # 如果精度不符合要求，则进行转换
	a = tf.cast(a,tf.float32) # tf.cast 函数可以完成精度转换
print('after :',a.dtype) # 打印转换后的精度
Out[15]:
before: <dtype: 'float16'>
after : <dtype: 'float32'>
#这样操作的意义在于针对某些只能处理特定精度的运算对数据进行预处理

1.2 字符串类型

tensorflow中的字符串类型数据可以认为就是C中的字符串类似，例如可以将图片路径保存为路径字符串，只需要传入字符串对象就能创建字符串类型的张量

1
2
3
4
In [8]:
a = tf.constant('Hello, Deep Learning.') # 创建字符串
Out[8]:
<tf.Tensor: id=17, shape=(), dtype=string, numpy=b'Hello, Deep Learning.'>

1.3 布尔类型

tensorflow引入布尔类型主要是为了能够方便地比较运算操作的结果，布尔类型的张量只需要传入 Python 语言的布尔类型数据，转换成 TensorFlow 内部布尔型即可

1
2
3
In [10]: a = tf.constant(True) # 创建布尔类型标量
Out[10]:
<tf.Tensor: id=22, shape=(), dtype=bool, numpy=True>
1
2
3
4
In [11]:
a = tf.constant([True, False]) # 创建布尔类型向量
Out[11]:
<tf.Tensor: id=25, shape=(2,), dtype=bool, numpy=array([ True, False])>

尽管可以使用python的布尔数据创建tensorflow的布尔数据，但是两者并不等价

1
2
3
4
5
6
7
In [11]:
a = tf.constant(True) # 创建 TF 布尔张量
a is True # TF 布尔类型张量与 python 布尔类型比较
a == True # 仅数值比较
Out[11]:
False # 对象不等价
<tf.Tensor: id=8, shape=(), dtype=bool, numpy=True> # 数值比较结果

1.4 Variable类型

为了区分需要计算梯度信息的张量与不需要计算梯度信息的张量，TensorFlow 增加了一种专门的数据类型来支持梯度信息的记录：tf.Variable。tf.Variable 类型在普通的张量类型基础上添加了 name，trainable 等属性来支持计算图的构建；

由于梯度运算会消耗大量的计算资源，而且会自动更新相关参数，对于不需要的优化的张量，如神经网络的输入𝒀，不需要通过 tf.Variable 封装；相反，对于需要计算梯度并优化的张量，如神经网络层的𝑿和𝒃，需要通过 tf.Variable 包裹以便 TensorFlow 跟踪相关梯度信息；

通过 tf.Variable()函数可以将普通张量转换为待优化张量（这个地方的待优化张量实际上就是1.x中的变量，但是2.x的变量意义仅在于支持梯度计算，所以我们呢不称之为变量而是Variable）

1
2
3
4
5
6
In [20]:
a = tf.constant([-1, 0, 1, 2]) # 创建 TF 张量
aa = tf.Variable(a) # 转换为 Variable 类型
aa.name, aa.trainable # Variable 类型张量的属性
Out[20]:
('Variable:0', True)

属性name和trainable是Variale特有的：

  • name 属性用于命名计算图中的变量，这套命名体系是 TensorFlow 内部维护的，一般不需要用户关注 name 属性；

  • trainable属性表征当前张量是否需要被优化，创建 Variable 对象时是默认启用优化标志，可以设置trainable=False 来设置张量不需要优化；

除了可以使用函数转换普通张量以得到Variable外，也可以直接创建Variable

1
2
3
4
In [21]:
a = tf.Variable([[1,2],[3,4]]) # 直接创建 Variable 张量
Out[21]:
<tf.Variable 'Variable:0' shape=(2, 2) dtype=int32, numpy=array([[1, 2],[3, 4]])>

2.创建张量

tensorflow中可以通过多种方式创建张量

2.1 数组、列表对象和张量

Numpy的array数组和python的list列表是非常重要的数据载体容器；

通过 tf.convert_to_tensor 函数可以创建新 Tensor，并将保存在 Python List 对象或者Numpy Array 对象中的数据导入到新 Tensor 中

1
2
3
4
5
In [22]:
tf.convert_to_tensor([1,2.]) # 从列表创建张量
Out[22]:
<tf.Tensor: id=86, shape=(2,), dtype=float32, numpy=array([1., 2.],
dtype=float32)>
1
2
3
4
In [23]:
tf.convert_to_tensor(np.array([[1,2.],[3,4]])) # 从数组中创建张量
Out[23]:
<tf.Tensor: id=88, shape=(2, 2), dtype=float64, numpy=array([[1., 2.],[3., 4.]])>#numpy的array浮点数组默认使用64bit精度，可以手动转换为32bit的精度保存在tensor中

事实上，tf.constant()和 tf.convert_to_tensor()都能够自动的把 Numpy 数组或者 Python列表数据类型转化为 Tensor 类型（所以我们选择其中一个使用即可）

2.2 创建全0/1张量

将张量创建为全 0 或者全 1 数据是非常常见的张量初始化手段；

通过 tf.zeros()和 tf.ones()即可创建任意形状，且内容全 0 或全 1 的张量；

1
2
3
4
In [24]: tf.zeros([]),tf.ones([]) # 创建全 0，全 1 的标量
Out[24]:
(<tf.Tensor: id=90, shape=(), dtype=float32, numpy=0.0>,
<tf.Tensor: id=91, shape=(), dtype=float32, numpy=1.0>)
1
2
3
4
In [25]: tf.zeros([1]),tf.ones([1]) # 创建全 0，全 1 的向量
Out[25]:
(<tf.Tensor: id=96, shape=(1,), dtype=float32, numpy=array([0.],dtype=float32)>,
<tf.Tensor: id=99, shape=(1,), dtype=float32, numpy=array([1.],dtype=float32)>)
1
2
3
4
5
6
7
In [26]: tf.zeros([2,2]) # 创建全 0 矩阵，指定 shape 为 2 行 2 列
Out[26]:
<tf.Tensor: id=104, shape=(2, 2), dtype=float32, numpy=array([[0., 0.],[0., 0.]], dtype=float32)>

In [27]: tf.ones([3,2]) # 创建全 1 矩阵，指定 shape 为 3 行 2 列
Out[27]:
<tf.Tensor: id=108, shape=(3, 2), dtype=float32, numpy=array([[1., 1.],[1., 1.],[1., 1.]], dtype=float32)>

通过 tf.zeros_like, tf.ones_like 可以方便地新建与某个张量 shape 一致，且内容为全 0 或全 1 的张量

1
2
3
4
5
6
7
8
9
In [28]: a = tf.ones([2,3]) # 创建一个矩阵
tf.zeros_like(a) # 创建一个与 a 形状相同，但是全 0 的新矩阵
Out[28]:
<tf.Tensor: id=113, shape=(2, 3), dtype=float32, numpy=array([[0., 0., 0.],[0., 0., 0.]], dtype=float32)>

In [29]: a = tf.zeros([3,2]) # 创建一个矩阵
tf.ones_like(a) # 创建一个与 a 形状相同，但是全 1 的新矩阵
Out[29]:
<tf.Tensor: id=120, shape=(3, 2), dtype=float32, numpy=array([[1., 1.],[1., 1.],[1., 1.]], dtype=float32)>

2.3 创建自定义数值张量

通过 tf.fill(shape, value)可以创建全为自定义数值 value 的张量，形状由 shape 参数指定

1
2
3
In [30]:tf.fill([], -1) # 创建-1 的标量
Out[30]:
<tf.Tensor: id=124, shape=(), dtype=int32, numpy=-1>

2.4 创建已知分布的张量

正态分布和均匀分布是最常见的分布之一，因此创建采样自这两种分布的张量非常有用（卷积神经网络中，卷积核张量𝑿初始化为正态分布有利于网络的训练）

通过 tf.random.normal(shape, mean=0.0, stddev=1.0)可以创建形状为 shape，均值为mean，标准差为 stddev 的正态分布𝒩(mean,stddev^2^)

1
2
3
In [33]: tf.random.normal([2,2]) # 创建标准正态分布的张量(均值为0，标准差为1，mean值默认是0，stddev值默认是1)
Out[33]:
<tf.Tensor: id=143, shape=(2, 2), dtype=float32, numpy=array([[-0.4307344 , 0.44147003],[-0.6563149 , -0.30100572]], dtype=float32)>

通过 tf.random.uniform(shape, minval=0, maxval=None, dtype=tf.float32)可以创建采样自[minval,maxval)区间的均匀分布的张量

1
2
3
In [35]: tf.random.uniform([2,2]) # 创建采样自[0,1)均匀分布的矩阵（minval默认值为0，maxval默认值为1）
Out[35]:
<tf.Tensor: id=158, shape=(2, 2), dtype=float32, numpy=array([[0.65483284, 0.63064325],[0.008816 , 0.81437767]], dtype=float32)>

如果需要均匀采样整形类型的数据，必须指定采样区间的最大值 maxval 参数，同时指定数据类型为 tf.int*型

1
2
3
4
In [37]: # 创建采样自[0,100)均匀分布的整型矩阵
tf.random.uniform([2,2],maxval=100,dtype=tf.int32)
Out[37]:
<tf.Tensor: id=171, shape=(2, 2), dtype=int32, numpy=array([[61, 21],[95, 75]])>

2.5 创建序列

在循环计算或者对张量进行索引时，经常需要创建一段连续的整型序列，可以通过tf.range()函数实现；

tf.range(limit, delta=1)可以创建[0,limit)之间，步长为 delta 的整型序列，不包含 limit 本身

1
2
3
In [38]: tf.range(10) # 0~10且步长为1，不包含 10
Out[38]:
<tf.Tensor: id=180, shape=(10,), dtype=int32, numpy=array([0, 1, 2, 3, 4, 5,6, 7, 8, 9])>

通过 tf.range(start, limit, delta=1)可以创建[start,limit)，步长为 delta 的序列，不包含limit 本身

1
2
3
In [40]: tf.range(1,10,delta=2) # 1~10
Out[40]:
<tf.Tensor: id=190, shape=(5,), dtype=int32, numpy=array([1, 3, 5, 7, 9])>

3.维度变换

（如果对于张量的基本意义还不太熟悉可能会觉得本节有点抽象，尽量理解）

假设我们有这样两个张量，b的shape为[3]，X的shape为[2,3]，现在我们需要计算X+b，也就是进行如下两个张量的计算

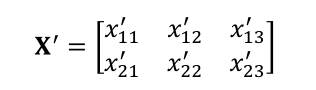
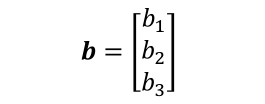
基本思想是讲shape为[3]的b偏置后按照样本数量进行复制，将其变成如下形式矩阵

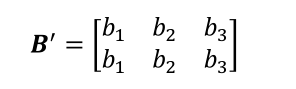
至此可以将两个shape相同的张量进行相加

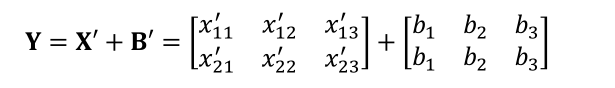
通过上面的例子我们大概知道，算法的每个模块对于数据张量的格式有不同的逻辑要求，当现有的数据格式不满足算法要求时，需要通过维度变换将数据调整为正确的格式，这就是维度变换的功能；

基本的维度变换操作函数包含了改变视图 reshape、插入新维度 expand_dims，删除维度 squeeze、交换维度 transpose、复制数据 tile 等函数；

3.1 改变视图

首先需要介绍张量的存储和视图这两个概念：

  • 视图：实际上就是我们理解张量的方式，如shape为[2,4,4,3]的张量A可以被理解为2张图片，每张图片4行4列，图片的每个位置(行,列)有RGB3个通道的数据；
  • 存储：张量在内存上被保存为一段连续的内存区域；

对于同样的存储，可以有不同的理解方式，进而产生不同的视图；

简单来说就是上述[2,4,4,3]的视图被理解为[2,48]一样是合理的，因为内存并不支持维度层级的概念，只能以平铺的方式按序写入内存，对于内存的层级关系需要人为管理：

  • shape中相对靠左侧的维度称为大维度；
  • shape中相对靠左侧的维度称为小维度；

当然改变视图需要在合法的操作下进行（默认前提是不会改变内存的存储，仅改变数据的逻辑结构）

从语法上来说，视图变换只需要满足新视图的元素总量与存储区域大小相等即可，正是因为极少的语法约束导致很容易在切换视图时出现逻辑隐患；

什么情况下的视图变换是不合法的呢？简单理解就是我们并没有按照维度的存储顺序来变换视图，这就将导致根据视图恢复数据的时候会出现问题；

例如根据“图片数量-行-列-通道”初始视图保存的张量，存储也是按照“图片数量-行-列-通道”的顺序写入的：

  • 如果按着“图片数量-像素-通道”的方式恢复数据，并没有与“图片数量-行-列-通道”相悖，因此能得到合法的数据；
  • 但是如果按着“图片数量-通道-像素”的方式恢复数据，由于内存布局是按着“图片数量-行-列-通道”的顺序，视图维度顺序与存储维度顺序相悖，提取的数据将是错乱的；

在 TensorFlow 中，可以通过张量的 ndim 和 shape 成员属性获得张量的维度数和形状

1
2
In [68]: x.ndim,x.shape # 获取张量的维度数和形状列表
Out[68]:(4, TensorShape([2, 4, 4, 3]))

通过 tf.reshape(x, new_shape)，可以将张量的视图任意地合法改变

1
2
3
4
5
In [69]: tf.reshape(x,[2,-1])#参数−1表示当前轴上长度需要根据张量总元素不变的法则自动推导，也就是48实际上是根据2*4*4*3/2得到
Out[69]:<tf.Tensor: id=520, shape=(2, 48), dtype=int32, numpy=
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
		16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,…
		80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95]])>

再次改变数据的视图为[2,4,12]

1
2
3
4
5
6
In [70]: tf.reshape(x,[2,4,12])
Out[70]:<tf.Tensor: id=523, shape=(2, 4, 12), dtype=int32, numpy=
array([[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],…
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]],
[[48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59], …
[84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95]]])>

3.2 增/删维度

增加维度：增加一个长度为1的维度相当于给原有的数据添加一个新维度的概念，维度长度为1，故数据并不需要改变，仅仅是改变数据的理解方式（这一点很有意思，其实不能说改变了理解方式，这相当于在原来的理解方式上增加新的理解而非改变理解方式，注意只有维度长度为1的时候才有这个结论），因此它其实可以理解为改变视图的一种特殊方式；

考虑给一张28*28的灰度图片数据保存为shape为[28,28]的张量，接着我们在末尾给该张量增加一个新的维度定义为通道维度数，则此时张量的shape变为[28,28,1]；

我们使用相同的方法在shape最前面插入一个新的维度，命名为图片数量维度，该维度长度为1，那么此时张量的shape变为[1,28,28,1]；

通过 tf.expand_dims(x, axis)可在指定的 axis 轴前可以插入一个新的维度

1
2
x = tf.expand_dims(x,axis=2) # axis=2 表示第三个维度前面的一个维度，使得shape成为[28,28,1]
x = tf.expand_dims(x,axis=0) # axis=0 表示在第一个维度之前插入新维度，使得shape变为[1,28,28,1]

tf.expand_dims的axis为正时，表示在当前维度之前插入一个新维度，为负时，表示当前维度之后插入一个新的维度；

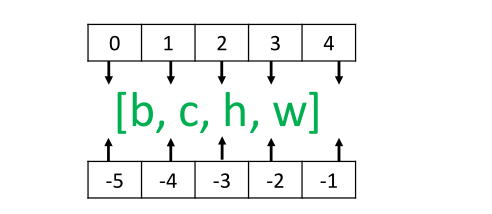
删除维度是增加维度的逆向操作与增加维度一样，删除维度只能删除长度为 1 的维度，也不会改变张量的存储；

如果希望将图片数量维度删除，可以通过 tf.squeeze(x, axis)函数

1
2
x = tf.squeeze(x, axis=0) # 删除图片数量维度得到[28,28,1]
x = tf.squeeze(x, axis=2) # 删除图片通道数维度得到[28,28]

如果不指定维度参数 axis，即 tf.squeeze(x)，那么它会默认删除所有长度为 1 的维度

可能有些读者还是觉得增加维度这个功能很鸡肋，我们举个直观的例子说明，现在我们有一个shape为[3]的张量b

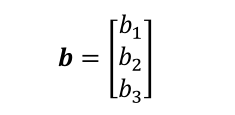
通过tf.expand_dims(b, axis=0)插入新维度，变成shape为[1,3]的张量B

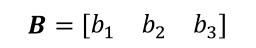
3.3 交换维度

尽管上述两个方法都不会影响张量的存储，但是仅仅改变张量的理解方式也就是改变视图实际上是不够用的，很多时候需要直接调整张量的存储顺序，该操作被称为交换维度；

交换维度操作是非常常见的，比如在TensorFlow中，图片张量的默认存储格式是通道后行格式：[b，h，w，c]，但是部分库的图片格式是通道先行格式：[b，c，h，w]，因此需要完成[b，h，w，c]到[b，c，h，w]维度交换运算，此时若简单的使用改变视图函数reshape，则新视图的存储方式需要改变（原因我们已经介绍过），因此使用改变视图函数是不合法的；

我们以[b，h，w，c]转换到[b，c，h，w]为例，介绍如何使用tf.transpose（x，perm）函数完成维度交换操作，其中参数perm表示新维度的顺序List；

考虑图片张量shape为[2,32,32,3]，”图片数量、行、列、通道数”的维度索引分别为0、1、2、3，如果需要交换为[b,c,h,w]格式，则新维度的排序为“图片数量、通道数、行、列”，对应的索引号为[0,3,1,2]，因此参数perm需设置为[0,3,1,2]，实现如下：

1
2
x = tf.random.normal([2,32,32,3])
tf.transpose(x,perm=[0,3,1,2]) # 交换维度

如果希望将[b,h,w,c]交换为[b,w,h,c]，即将高、宽维度互换，则新维度索引为[0,2,1,3]

1
2
x = tf.random.normal([2,32,32,3])
tf.transpose(x,perm=[0,2,1,3]) # 交换维度

需要注意的是，通过 tf.transpose 完成维度交换后，张量的存储顺序已经改变，视图也随之改变，后续的所有操作必须基于新的存续顺序和视图进行；

3.4 复制数据

当通过增加维度操作插入新维度后，可能希望在新的维度上面复制若干份数据以满足后续算法的格式要求；

考虑前面的例子，我们在新维度上复制了Batch size份数据才能构造一个完整的shape为[2,3]的张量

可以通过 tf.tile(x, multiples)函数完成数据在指定维度上的复制操作，multiples分别指定了每个维度上面的复制倍数，对应位置为1表明不复制，为2表明新长度为原来长度的2倍，即数据复制一份，以此类推；

在实际实验中我们并不需要手动增加维度并复制数据，这些操作tensorflow会自动完成（这就是tensorflow的自动扩展功能，且该功能优于手动增加、复制）；

需要注意的是，tf.tile 会创建一个新的张量来保存复制后的张量，由于复制操作涉及大量数据的读写 IO 运算，计算代价相对较高。神经网络中不同 shape 之间的张量运算操作十分频繁，那么有没有轻量级的复制操作呢？这就是接下来要介绍的 Broadcasting 操作

4.Broadcasting

Broadcasting 称为广播机制(或自动扩展机制)，它是一种轻量级的张量复制手段，在逻辑上扩展张量数据的形状，但是只会在需要时才会执行实际存储复制操作。对于大部分场景，Broadcasting 机制都能通过优化手段避免实际复制数据而完成逻辑运算，从而相对于tf.tile 函数，减少了大量计算代价；Broadcasting 会通过深度学习框架的优化手段避免实际复制数据而完成逻辑运算，至于怎么实现的用户不必关心；

1
2
3
4
x = tf.random.normal([2,4])
w = tf.random.normal([4,3])
b = tf.random.normal([3])
y = x@w+b # 不同 shape 的张量直接相加

上述运算在tensorflow中是合法的，因为它自动调用 Broadcasting函数 tf.broadcast_to(x, new_shape)，将b的shape扩展为与x@w的shape相同的[2,3]

Broadcasting 机制并不会扰乱正常的计算逻辑，它只会针对于最常见的场景自动完成增加维度并复制数据的功能

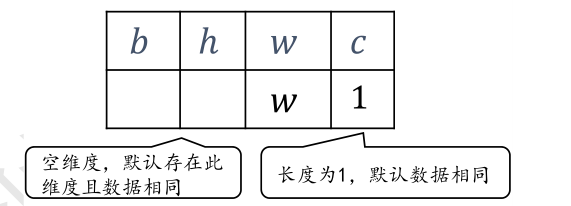
当然broadcasting机制不是万能的，在对两个shape右对齐后它需要进行普适性判断：

  • 对于长度为 1 的维度，默认这个数据普遍适合于当前维度的其他位置；

  • 对于不存在的维度，则在增加新维度后默认当前数据也是普适于新维度的，从而可以扩展为更多维度数、任意长度的张量形状，如[32,1]可以直接broadcasting为[2,32,32,4]；

  • 对于已经存在且长度不为1的维度则不符合普适性原则如[32,2]不能直接broadcasting为[2,32,32,4]

5.数学运算

本节介绍tensorflow中常见的数学运算函数；

5.1 四则运算

加、减、乘、除是最基本的数学运算，分别通过 tf.add, tf.subtract, tf.multiply, tf.divide函数实现，TensorFlow 已经重载了+、 −、 ∗ 、/运算符，一般推荐直接使用运算符来完成加、减、乘、除运算；整除和余除也是常见的运算之一，分别通过//和%运算符实现；

1
2
3
4
5
6
In [89]:
a = tf.range(5)
b = tf.constant(2)
a//b # 整除运算
Out[89]:
<tf.Tensor: id=115, shape=(5,), dtype=int32, numpy=array([0, 0, 1, 1, 2])>
1
2
3
In [90]: a%b # 余除运算
Out[90]:
<tf.Tensor: id=117, shape=(5,), dtype=int32, numpy=array([0, 1, 0, 1, 0])>

乘方运算可以通过tf.pow(x,a)完成，也可以使用运算符**完成

1
2
3
4
5
In [91]:
x = tf.range(4)
tf.pow(x,3) # 乘方运算
Out[91]:
<tf.Tensor: id=124, shape=(4,), dtype=int32, numpy=array([ 0, 1, 8, 27])>
1
2
3
In [92]: x**2 # 乘方运算符
Out[92]:
<tf.Tensor: id=127, shape=(4,), dtype=int32, numpy=array([0, 1, 4, 9])>

如果我们将指数设置为分数，则可以实现开方运算

1
2
3
4
In [93]: x=tf.constant([1.,4.,9.])
x**(0.5) # 平方根
Out[93]:
<tf.Tensor: id=139, shape=(3,), dtype=float32, numpy=array([1., 2., 3.],dtype=float32)>

特别地，对于常见的平方和平方根运算，可以使用 tf.square(x)和 tf.sqrt(x)实现；

5.2 指数和对数运算

指数运算可以通过tf.pow(x,a)完成，也可以使用运算符**完成（因为乘方x^a^和指数运算a^x^都是相同的形式，只是参数的位置不同）

1
2
3
4
In [96]: x = tf.constant([1.,2.,3.])
2**x # 指数运算
Out[96]:
<tf.Tensor: id=179, shape=(3,), dtype=float32, numpy=array([2., 4., 8.],dtype=float32)>

特别地，对于自然指数e^x^ ，可以通过tf.exp(x)实现；

在TensorFlow中，自然对数logex可以通过 tf.math.log(x)实现

1
2
3
4
In [98]: x=tf.exp(3.)#自然指数运算
tf.math.log(x) 		 #对数运算
Out[98]:
<tf.Tensor: id=186, shape=(), dtype=float32, numpy=3.0>

如果需要计算其他底数的对数，需要使用对数的换底公式

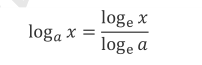
间接性实现（当然这本书是2019年写的，2022年应该已经具备直接计算其他底数的对数的函数了）；

5.3 矩阵乘法

其实这里称作张量乘法更加合适；

可以通过@运算符或者tf.matmul(a,b)函数实现矩阵乘法，tensorflow中的矩阵支持批量方式，也就是张量A和B的维度数可以大于2，此时tensorflow会选择A和B的最后两个维度进行矩阵相乘，将前面所有的维度都视作batch维度；

根据矩阵相乘的定义，𝑩和𝑪能够矩阵相乘的条件是，𝑩的倒数第一个维度长度(列)和𝑪的倒数第二个维度长度(行)必须相等，比如张量a shape:[4,3,28,32]可以与张量b shape:[4,3,32,2]进行矩阵相乘；

当然张量乘法函数同样支持broadcasting机制

1
2
3
a = tf.random.normal([4,28,32])
b = tf.random.normal([32,16])
tf.matmul(a,b) #首先会将b拓展为shape[4,32,16]，再与张量a进行批量形式地矩阵相乘，得到结果的shape为[4,28,16]

第二章 tensorflow2.x进阶

1.合并与分割

1.1 拼接与堆叠

合并是指将多个张量在某个维度上合并为一个张量；

以某学校班级成绩册数据为例，设张量𝑩保存了某学校 1~4 号班级的成绩册，每个班级 35 个学生，共 8 门科目成绩，则张量𝑩的 shape 为：[4,35,8]；同样的方式，张量𝑪保存了其它 6 个班级的成绩册，shape 为[6,35,8]。通过合并这 2 份成绩册，便可得到学校所有班级的成绩册，记为张量𝑫，shape 应为[10,35,8]，其中，10 代表 10 个班级，35 代表 35 个学生，8 代表 8 门科目。这就是张量合并的意义所在；

张量的合并可以使用拼接(Concatenate)和堆叠(Stack)操作实现：

  • 拼接操作并不会产生新的维度，仅在现有的维度上合并，而堆叠会创建新维度；

选择使用拼接还是堆叠操作来合并张量，取决于具体的场景是否需要创建新维度；

在 TensorFlow 中，可以通过 tf.concat(tensors, axis)函数拼接张量，其中参数tensors 保存了所有需要合并的张量 List，axis 参数指定需要合并的维度索引

1
2
3
a = tf.random.normal([4,35,8]) # 模拟成绩册 A
b = tf.random.normal([6,35,8]) # 模拟成绩册 B
tf.concat([a,b],axis=0) # 拼接合并成绩册，因为班级维度索引号为0，所以axis=0

从语法上来说，拼接合并操作可以在任意的维度上进行，唯一的约束是非合并维度的长度必须一致。比如 shape为[4,32,8]和shape为[6,35,8]的张量不能直接在班级维度上进行合并，因为学生数量维度的长度并不一致，一个为32，另一个为35；

使用 tf.stack(tensors, axis)可以堆叠方式合并多个张量，通过 tensors 列表表示，参数axis 指定新维度插入的位置，axis 的用法与 tf.expand_dims 的一致：

  • 当axis ≥ 0时，在axis之前插入；
  • 当axis < 0时，在axis之后插入新维度；

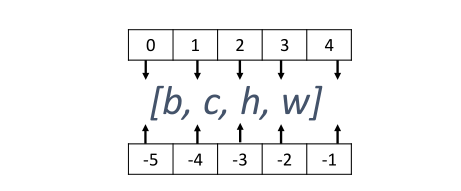
如果想要在合并的时候创建一个新的维度，就需要使用堆叠；

考虑张量𝑩保存了某个班级的成绩册，shape 为[35,8]，张量𝑪保存了另一个班级的成绩册，shape 为[35,8]。合并这 2 个班级的数据时，则需要创建一个新维度，定义为班级维度，新维度可以选择放置在任意位置，一般根据大小维度的经验法则，将较大概念的班级维度放置在学生维度之前；

1
2
3
a = tf.random.normal([35,8])
b = tf.random.normal([35,8])
tf.stack([a,b],axis=0) # 堆叠合并为 2 个班级，班级维度插入在最前

tf.stack 也需要满足张量堆叠合并条件，它需要所有待合并的张量 shape 完全一致才可合并；

1.2 分割

合并操作的逆过程就是分割，将一个张量分拆为多个张量。继续考虑成绩册的例子，我们得到整个学校的成绩册张量，shape 为[10,35,8]，现在需要将数据在班级维度切割为10 个张量，每个张量保存了对应班级的成绩册数据；

通过 tf.split(x, num_or_size_splits, axis)可以完成张量的分割操作：

  • x 参数：待分割张量。
  • num_or_size_splits 参数：切割方案。当 num_or_size_splits 为单个数值时，如 10，表示等长切割为 10 份；当 num_or_size_splits 为 List 时，List 的每个元素表示每份的长度，如[2,4,2,2]表示切割为 4 份，每份的长度依次是 2、4、2、2。
  • axis 参数：指定分割的维度索引号

上述成绩册分割的例子代码如下

1
2
3
4
5
6
In [8]:
x = tf.random.normal([10,35,8])
# 等长切割为 10 份
result = tf.split(x, num_or_size_splits=10, axis=0)
len(result) # 返回的列表为包含切割后的 10 个张量的列表，result[0]表示第一个班级的成绩册数据，其shape为[1,35,8]
Out[8]: 10

注意：使用split切割不等于降维，切割后的张量仍然保持了先前的维度；

特别地，如果希望在某个维度上全部按长度为 1 的方式分割，还可以使用 tf.unstack(x,axis)函数。这种方式是 tf.split 的一种特殊情况，切割长度固定为 1，只需要指定切割维度的索引号即可

1
2
3
4
In [11]: x = tf.random.normal([10,35,8])
result = tf.unstack(x,axis=0) # Unstack 为长度为 1 的张量
len(result) # 返回 10 个张量的列表
Out[11]: 10

注意：使用unstack切割会导致维度消失，这也是它和split的区别；

2.统计属性

在计算过程中，经常需要统计数据的各种属性如均值、范数等信息，之所以要获取这些信息是因为张量一般都很庞大，直接观察很难获取有用信息，通过获取这些张量的统计属性可以较轻松地推测张量数值的分布；

2.1 向量范数

向量范数(Vector Norm)是表征向量“长度”的一种度量方法，它可以推广到张量上，在神经网络中，常用来表示张量的权值大小，梯度大小等；

  • L1 范数，定义为向量𝒙的所有元素绝对值之和

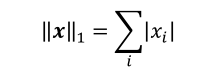
  • L2 范数，定义为向量𝒙的所有元素的平方和开根号

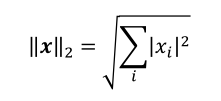
  • ∞ 范数，定义为向量𝒙的所有元素绝对值的最大值

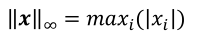
尽管上述公式都是针对向量的，在应对矩阵和张量时都可以将其平铺为向量再进行范数的计算；

在 TensorFlow 中，可以通过 tf.norm(x, ord)求解张量的 L1、L2、∞ 等范数，其中参数ord 指定为 1、2 时计算 L1、L2 范数，指定为 np.inf 时计算∞ 范数

2.2 最值、均值

通过 tf.reduce_max、tf.reduce_min、tf.reduce_mean、tf.reduce_sum 函数可以求解张量在某个维度上的最大、最小、均值、和，也可以求全局最大、最小、均值、和信息

当不指定 axis 参数时，tf.reduce_*函数会求解出全局元素的最大、最小、均值、和等数据

通过 tf.argmax(x, axis)和 tf.argmin(x, axis)可以求解在 axis 轴上，x 的最大值、最小值所在的索引号

3.张量比较

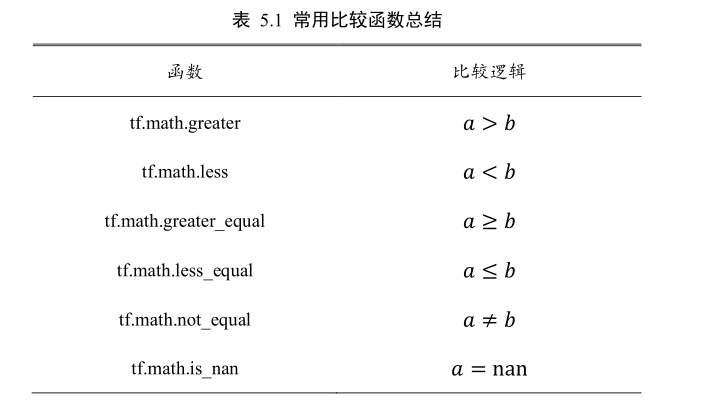
4.数据限幅

现在考虑如何实现非线性激活函数ReLu(这个函数的本质很简单，就是最小数值为0)，可以通过数据限幅实现，只需要限制元素的范围𝑦 ∈ [0,+∞)即可；

在 TensorFlow 中，可以通过 tf.maximum(x, a)实现数据元素的下限幅，即𝑦 ∈ [𝑏,+∞)；可以通过 tf.minimum(x, a)实现数据元素的上限幅，即𝑦 ∈ (−∞,𝑏]

1
2
3
In [33]:x = tf.range(9)
tf.maximum(x,2) # 下限幅到 2
Out[33]:<tf.Tensor: id=48, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3,4, 5, 6, 7, 8])>
1
2
In [34]:tf.minimum(x,7) # 上限幅到 7
Out[34]:<tf.Tensor: id=41, shape=(9,), dtype=int32, numpy=array([0, 1, 2, 3,4, 5, 6, 7, 7])>

通过组合 tf.maximum(x, a)和 tf.minimum(x, b)可以实现同时对数据的上下边界限幅，即𝑦 ∈ [𝑏,𝑐]

1
2
3
In [35]:x = tf.range(9)
tf.minimum(tf.maximum(x,2),7) # 限幅为 2~7
Out[35]:<tf.Tensor: id=57, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3,4, 5, 6, 7, 7])>

更方便地，我们可以使用 tf.clip_by_value 函数实现上下限幅

1
2
3
In [36]:x = tf.range(9)
tf.clip_by_value(x,2,7) # 限幅为 2~7
Out[36]:<tf.Tensor: id=66, shape=(9,), dtype=int32, numpy=array([2, 2, 2, 3,4, 5, 6, 7, 7])>

现在我们解决刚开始的问题，实现一个ReLu函数，只需要使用到maximum

1
2
def relu(x): # ReLU 函数
	return tf.maximum(x,0.) # 下限幅为 0 即可

第三章 tensorflow2.x高级

本章我们主要介绍如何将神经网络、机器学习等抽象的概念用tensorflow实现（这一章很有可能需要手写并进行纸上演算，需要非常多的推导，需要耐心）；

我其实一直有一个问题，为什么这些教材都只是教我们怎么调用API，但是对于一些语法规则只字不提，比如说为什么要用with，为什么要用def？这些问题如果不自行上网搜索根本就找不到；

1.数据可视化

首先我们介绍一下tensorflow中tensorboard包的使用，这个可视化工具在机器学习的训练过程中尤其重要；（尽管现在我并不知道tensorboard是否会受到tensorflow版本的不同带来的影响）

注意一个很容易混淆的点就是，数据可视化不完全等于简单的调用matplotlib库画出数据曲线，当我们面对一些高级的过程时就需要选择tensorboard工具；

（关键是市面上的tensorboard教程真的好少啊我的天，真是无语了…)

参考链接:

tensorboard作为tensorflow的可视化工具，通过TensorFlow程序运行过程中产生的日志文件来对TensorFlow的程序运行状态进行可视化，它与TensorFlow跑在两个不同的进程中；

TensorBoard不需要额外安装，在TensorFlow安装时已自动完成，在Anaconda Prompt中先进入日志存放的目录（非常重要），再运行TensorBoard，并将日志的地址指向程序日志输出的地址；

启动服务的端口默认为6006；使用 –port 参数可以改编启动服务的端口，TensorBoard是一个在本地启动的服务，启动完成后在浏览器网址：http://localhost:6006即可进行访问；

下面是一些常用的tensorboard API

TensorBoard提供了很多种数据类型的显示：

  • 标量通过tf.summary.scalar()函数显示；

  • 图像通过tf.summary.image()函数显示；

  • 声音通过tf.summary.audio()函数显示；

  • 张量通过tf.summary.histogram()函数显示；

这些摘要的操作定义完毕后，可以通过tf.summary.merge_all()函数把它们合并起来，合并后的摘要操作就可以通过session来运行，得到摘要信息（summary_str），通过FileWrite写入事件日志文件中；

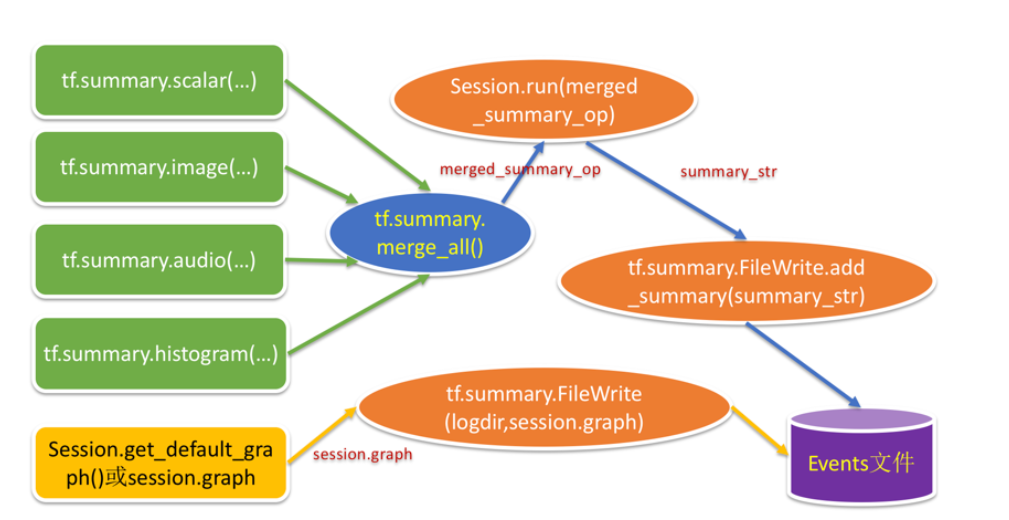
tensorflow包的大致使用流程如下：

  1. 设置保存路径: tenboard_dir = ‘./MNIST’
  2. 指定⽂件⽤来保存TensorFlow的图（分为train和test图）
  3. 把图add保存在本地磁盘
  4. 进⼊⽣成的events⽂件的上⼀级⽂件夹⽬录中，如在DOS窗⼝运⾏命令： tensorboard --logdir=test 或 tensorboard --logdir=train
  5. 复制终端返回的⽹址，使⽤浏览器进⼊该⽹址

1.1 启动tensorboard

本地启动tensorboard使用命令行运行

1
tensorboard --logdir=<directory_name>

注意将directory_name标记替换为保存数据的目录，默认是’logs’；

使用其他端口开启服务

1
tensorboard --logdir=test --host=127.0.0.1 --port=8008

当然也可以在jupyter notebook中使用tensorboard，使用以下命令

1
%load_ext tensorboard

运行上述代码将加载 TensorBoard并允许我们将其用于可视化，加载扩展后，我们现在可以启动 TensorBoard：

1
%tensorboard --logdir logs

（在jupyter notebook中启动几乎是不可能成功的…一直显示端口被占用）

2.tensorflow文本文件

参考链接：

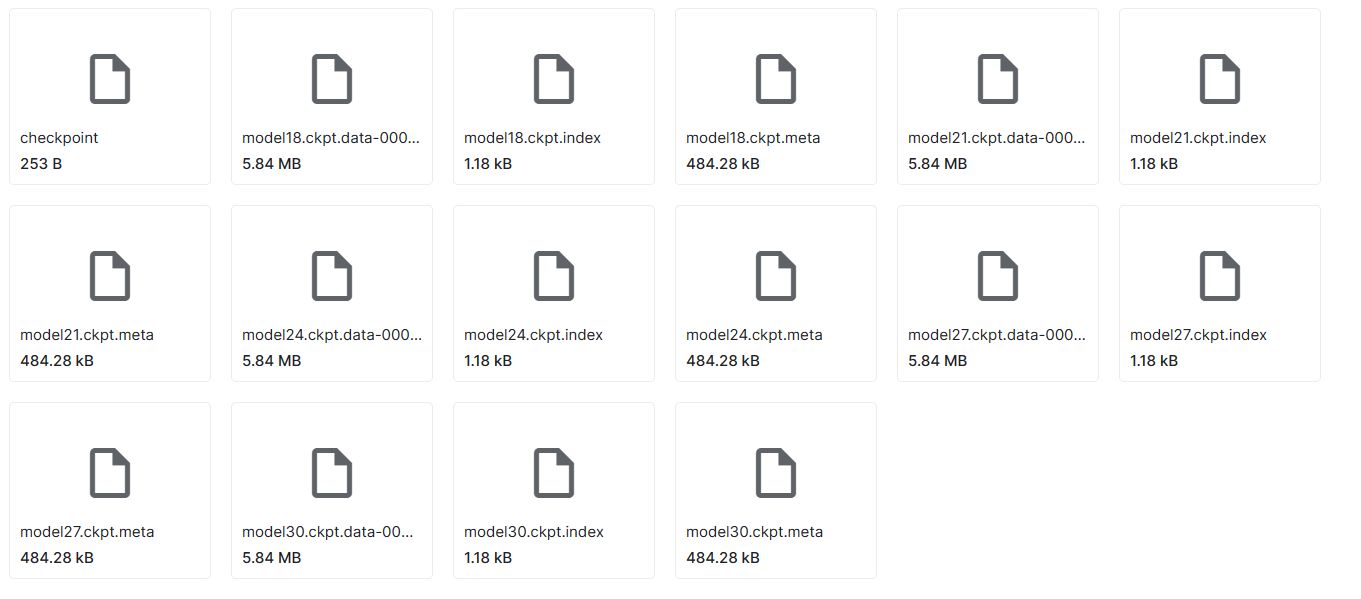
checkpoint也称为检查点，保存了一个目录下所有的模型文件列表，存储着模型model使用的所有的tf.Variable 对象以及模型结构的定义；

  • checkpoint文件：文本文件，可直接用文本编辑器打开，记录了训练过程中在所有中间节点上保存的模型的名称，首行记录的是最后（最近）一次保存的模型名称；
  • data文件：数据文件，保存的是网络的权值，偏置，操作等；
  • index文件：index文件本质上是一个不可变的字符串表，每一个键都是张量的名称，它的值是一个序列化的BundleEntryProto。 每个BundleEntryProto描述张量的元数据：“数据”文件中的哪个文件包含张量的内容，该文件的偏移量，校验和，一些辅助数据等；
  • meta文件：meta文件保存的是图结构，通俗地讲就是神经网络的网络结构，一般而言网络结构是不会发生改变，所以可以只保存一个；
1
2
# 使用如下代码只在第一次保存meta文件
saver.save(sess, 'my_model.ckpt', global_step=step, write_meta_graph=False)
1
2
# 使用如下代码恢复整个graph结构
tf.train.import_meta_graph(‘xxxxxx.meta’)
自学课程
#机器学习 #python
Tensorflow
https://gintoki-jpg.github.io/2022/10/13/工具_tensorflow/
作者
杨再俨
发布于
2022年10月13日
许可协议