初级项目_语法分析器

源码以及相关参考资料已经上传至github：https://github.com/Gintoki-jpg/lexer-parser

绪论

实验题目：语法分析器

实验内容：编写语法分析程序，实现对算术表达式的语法分析，要求所分析算数表达式由如下的文法G产生

文法G的产生式如下：

1
2
3
4
5
E→E + T | E - T | T

T→T * F | T / F | F

F→(E) | num

实验要求：在对输入的算术表达式进行分析的过程中，依次输出所采用的产生式；

因为实际情况，我们并没有选择利用YACC自动生成语法分析程序

  • 自顶向下的分析：

    • 编程实现算法 4.2，为给定文法自动构造预测分析表；

    • 编程实现算法 4.1，构造 LL(1) 预测分析程序；

  • 自底向上的分析：

    • 构造识别该文法所有活前缀的 DFA；

    • 构造该文法的 LR 分析表；

    • 编程实现算法 4.3，构造 LR 分析程序；

（可能很多人看不懂这个实验要求，实际上就是一共实现三个算法4.2，4.1和4.3）

一、自顶向下的分析

1.构造预测分析表

1.1 概述

在实现之前我们先回忆一下自顶向下和ll(1)语法相关知识点；

ll(1)文法是构造不带回溯的自上而下的分析的必要条件，我们对ll(1)文法的定义如下

如果不是ll(1)文法那就根本用不了自上而下的分析方法，需要我们之后用自下向上的分析方法解决；

我们应当如何将一个普通的文法改造为ll(1)文法进行自上而下的分析呢？主要使用以下步骤：

  1. 消除文法的左递归；
  2. 提取左公共因子；
  3. 计算产生式右部的First集合和产生式左部的Follow集合；
  4. 如果原文法为ll(1)文法，使用LL1文法的分析进行自顶向下的不带回溯的分析；

之所以必须使用ll(1)文法进行自上而下的分析，是因为在使用ll(1)文法对符号串进行自上而下的推导(匹配)的时候，可以明确唯一的选择产生式，也就对应了预测分析表中的唯一一个选项；

给定一个ll(1)文法就能唯一构造一个预测分析表，下面我们介绍怎么根据所给的ll(1)文法来构造一个预测分析表，实际就是使用算法4.2，我们将算法4.2的伪代码转换为自然语言：

构造文法G的分析表M[A,o]，确定每个产生式A->a在表中的位置：

  • 对每个终结符o属于FIRST(a) ，把A→a加至M[A，o]中；

  • 若空串属于FIRST(a)，则对任何 b属于FOLLOW(A) 把A→a加至M[A，b]中；

  • 对文法G的每个产生式A→a执行第1步和第2步；

  • 把所有无定义的M[A，o]标上“出错标志”；

1.2 程序实现

构造预测分析表的流程图如下

我们需要手动计算一下相关的First集和Follow集

根据上述规则构造的预测分析表如下，我们到时候也可以根据这个结果检查我们的程序是否编写正确

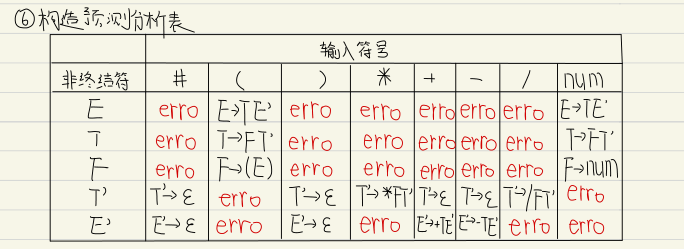
1.2.1 模块设计

我们主要需要用到以下的类和容器：

1
2
3
4
5
6
7
8
9
10
11
class Syntax_Analyzer{                               //语法分析器类，这个类是整个程序的核心，包含了所有核心函数，所有语法分析需要进行的动作都只能通过它发起，类似一个接口;
public:
    PREDICT_TABLE create_predict_table(GRAMMAR_TABLE G, FIRST_TABLE first_table, FOLLOW_TABLE follow_table);    //创建一个预测分析表
    void print_predict_table(PREDICT_TABLE predict_table);                                                      //输出预测分析表
    ANALYZE_TABLE create_analyze_table(string input_string, PREDICT_TABLE M);                                   //根据预测分析表开始进行语法分析(ll(1)非递归预测分析)
    void print_analyze_table(ANALYZE_TABLE analyze_table);                                                      //输出非递归预测分析的过程，即非递归预测分析对象
    void error(string error_string)                                                                             //输出错误字符串/错误信息
    {
        cout << error_string << endl;
    };
};
1
typedef map<string, vector<string>> FIRST_TABLE;  //First集合
1
typedef map<string, vector<string>> FOLLOW_TABLE; //Follow集合
1
typedef vector<vector<string>> ANALYZE_TABLE;     //ll(1)语法分析表，第二阶段输出分析过程的时候使用
1
2
3
4
5
6
7
class GRAMMAR_TABLE{                                //语法表，用于保存所给的文法的相关信息
public:
    map<string, vector<string>> production;        //产生式
    vector<string> nonterminal;                     //非终结符
    vector<string> terminator;                      //终结符
    string start_symbol;                             //起始符号
};
1
2
3
4
5
6
7
class PREDICT_TABLE{                                //预测分析表，这是我们第一阶段需要构造的表
public:
    map<string, map<string, string>> table;      //预测分析表
    vector<string> nonterminal;                   //非终结符
    vector<string> terminator;                    //终结符
    string start_symbol;                           //起始符号
};

1.2.2 函数封装

(1)全局初始化函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
void Syntax_Analyzer::global_init(GRAMMAR_TABLE &G, FIRST_TABLE &first_table, FOLLOW_TABLE &follow_table)
{
    //1.初始化每个非终结符能够产生的所有推导结果集合（即产生式集合）
    //这里由于使用E'这种形式会变成双字符不利于后续处理，所以我们将E'变为了G，将T'变成了U
    vector<string> E_vector;
    E_vector.push_back("TG");
    G.production.insert(pair<string, vector<string>>("E", E_vector));

    vector<string> G_vector;
    G_vector.push_back("+TG");
    G_vector.push_back("-TG");
    G_vector.push_back("ε");
    G.production.insert(pair<string, vector<string>>("G", G_vector));

    vector<string> T_vector;
    T_vector.push_back("FU");
    G.production.insert(pair<string, vector<string>>("T", T_vector));

    vector<string> U_vector;
    U_vector.push_back("*FU");
    U_vector.push_back("/FU");
    U_vector.push_back("ε");
    G.production.insert(pair<string, vector<string>>("U", U_vector));

    vector<string> F_vector;
    F_vector.push_back("(E)");
    F_vector.push_back("id");
    G.production.insert(pair<string, vector<string>>("F", F_vector));
    //2.初始化所有终结符和非终结符
    G.nonterminal.push_back("E");
    G.nonterminal.push_back("G");
    G.nonterminal.push_back("T");
    G.nonterminal.push_back("U");
    G.nonterminal.push_back("F");
    G.terminator.push_back("+");
    G.terminator.push_back("-");
    G.terminator.push_back("*");
    G.terminator.push_back("/");
    G.terminator.push_back("(");
    G.terminator.push_back(")");
    G.terminator.push_back("id");
    G.terminator.push_back("$");
    G.start_symbol = "E";
    //3.初始化每个非终结符对应的First集合与Follow集合
    vector<string> E_first_vector;
    E_first_vector.push_back("(");
    E_first_vector.push_back("id");
    first_table.insert(pair<string, vector<string>>("E", E_first_vector));

    vector<string> G_first_vector;
    G_first_vector.push_back("+");
    G_first_vector.push_back("-");
    G_first_vector.push_back("ε");
    first_table.insert(pair<string, vector<string>>("G", G_first_vector));

    vector<string> T_first_vector;
    T_first_vector.push_back("(");
    T_first_vector.push_back("id");
    first_table.insert(pair<string, vector<string>>("T", T_first_vector));

    vector<string> U_first_vector;
    U_first_vector.push_back("*");
    U_first_vector.push_back("/");
    U_first_vector.push_back("ε");
    first_table.insert(pair<string, vector<string>>("U", U_first_vector));

    vector<string> F_first_vector;
    F_first_vector.push_back("(");
    F_first_vector.push_back("id");
    first_table.insert(pair<string, vector<string>>("F", F_first_vector));

    vector<string> E_follow_vector;
    E_follow_vector.push_back("$");
    E_follow_vector.push_back(")");
    follow_table.insert(pair<string, vector<string>>("E", E_follow_vector));

    vector<string> G_follow_vector;
    G_follow_vector.push_back("$");
    G_follow_vector.push_back(")");
    follow_table.insert(pair<string, vector<string>>("G", G_follow_vector));

    vector<string> T_follow_vector;
    T_follow_vector.push_back("+");
    T_follow_vector.push_back("-");
    T_follow_vector.push_back("$");
    T_follow_vector.push_back(")");
    follow_table.insert(pair<string, vector<string>>("T", T_follow_vector));

    vector<string> U_follow_vector;
    U_follow_vector.push_back("+");
    U_follow_vector.push_back("-");
    U_follow_vector.push_back("$");
    U_follow_vector.push_back(")");
    follow_table.insert(pair<string, vector<string>>("U", U_follow_vector));

    vector<string> F_follow_vector;
    F_follow_vector.push_back("*");
    F_follow_vector.push_back("/");
    F_follow_vector.push_back("+");
    F_follow_vector.push_back("-");
    F_follow_vector.push_back("$");
    F_follow_vector.push_back(")");
    follow_table.insert(pair<string, vector<string>>("F", F_follow_vector));
}
(2)创建预测分析表函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
PREDICT_TABLE Syntax_Analyzer::create_predict_table(GRAMMAR_TABLE G, FIRST_TABLE first_table, FOLLOW_TABLE follow_table)
{
    PREDICT_TABLE M;
    //加入所有非终结符
    M.table.insert(pair<string, map<string, string>>("E", map<string, string>()));
    M.table.insert(pair<string, map<string, string>>("G", map<string, string>()));
    M.table.insert(pair<string, map<string, string>>("T", map<string, string>()));
    M.table.insert(pair<string, map<string, string>>("U", map<string, string>()));
    M.table.insert(pair<string, map<string, string>>("F", map<string, string>()));
    //遍历G的production，根据first集合和follow集合填空
    for (auto iter = G.production.begin(); iter != G.production.end(); iter++)
    {
        string A = iter->first;//iter指向的对象production是一个<string, vector<string>>，分别使用first和second迭代遍历string和vector对象
        for (auto iter2 = iter->second.begin(); iter2 != iter->second.end(); iter2++)
        {
            string alpha = *iter2;
            if (alpha[0] >= 'A' && alpha[0] <= 'Z') //如果vector中的元素的第一个字符是大写字母如"FU"
            {
                vector<string> first_vector = first_table.find(string(1, alpha[0]))->second;    //根据first集合构造预测分析表
                for (auto a = first_vector.begin(); a != first_vector.end(); a++)
                {
                    if (*a != "ε")
                    {
                        M.table.find(A)->second.insert(pair<string, string>(*a, alpha));
                    }
                }
                if (find(first_vector.begin(), first_vector.end(), "ε") != first_vector.end()) //假如ε属于first(产生式右部符号)
                {
                    vector<string> follow_vector = follow_table.find(A)->second;
                    for (auto b = follow_vector.begin(); b != follow_vector.end(); b++)
                    {
                        if (*b != "ε")
                        {
                            M.table.find(A)->second.insert(pair<string, string>(*b, alpha));
                        }
                    }
                }
            }
            else
            {
                string alpha_first;
                if (start_pattern(alpha, "id"))        //如果产生式右部以id开头则将first赋值为id(之所以不与else合并是因为id是两个字符，不符合alpha[0]的要求)
                {
                    alpha_first = "id";
                }
                else if (start_pattern(alpha, "ε"))
                {
                    alpha_first = "ε";
                }
                else
                {
                    alpha_first = alpha[0];
                }

                if (alpha_first != "ε")
                {
                    M.table.find(A)->second.insert(pair<string, string>(alpha_first, alpha));
                }
                if (alpha_first == "ε")
                {
                    vector<string> follow_vector = follow_table.find(A)->second;
                    for (auto b = follow_vector.begin(); b != follow_vector.end(); b++)
                    {
                        if (*b != "ε")
                        {
                            M.table.find(A)->second.insert(pair<string, string>(*b, alpha));
                        }
                    }
                }
            }
        }
    }
    //遍历G的非终结符，将上一步填充的对应产生式insert到M的table中，若没有对应的产生式则填入"error"
    for (auto iter = G.nonterminal.begin(); iter != G.nonterminal.end(); iter++)
    {
        string A = *iter;
        for (auto iter2 = G.terminator.begin(); iter2 != G.terminator.end(); iter2++)
        {
            string a = *iter2;
            if (M.table.find(A)->second.find(a) == M.table.find(A)->second.end())
            {
                M.table.find(A)->second.insert(pair<string, string>(a, "error"));
            }
        }
    }
    M.nonterminal = G.nonterminal;
    M.terminator = G.terminator;
    M.start_symbol = G.start_symbol;
    cout<<"Predict table build successfully!"<<endl;
    return M;
}

(3)输出预测分析表函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void Syntax_Analyzer::print_predict_table(PREDICT_TABLE M)
{
    cout << "\t\t\t\t<====================Predict table====================>" << endl;
    cout << "\t";
    for (auto iter : M.table.begin()->second)
    {
        cout << iter.first << "\t\t";
    }
    cout << endl;
    for (auto iter = M.table.begin(); iter != M.table.end(); iter++)
    {
        cout << iter->first << "\t";
        for (auto iter2 = iter->second.begin(); iter2 != iter->second.end(); iter2++)
        {
            string output_str;
            if (iter2->second == "error")
            {
                output_str = "error";
            }
            else if (iter2->second == "ε")
            {
                output_str = iter->first + "-><epsilon>";
            }
            else
            {
                output_str = iter->first + "->" + iter2->second;
            }
            if (output_str.length() >= 8)
            {
                cout << output_str << "\t";
            }
            else
            {
                cout << output_str << "\t\t";
            }
        }
        cout << endl;
    }
}

2.非递归预测分析

2.1 概述

假设我们已经有了预测分析表和待分析的符号串，下面需要做的就是根据算法4.1完成非递归预测分析

下面我们简单举一个例子展示

我们的程序最终应当是具备如下形式的

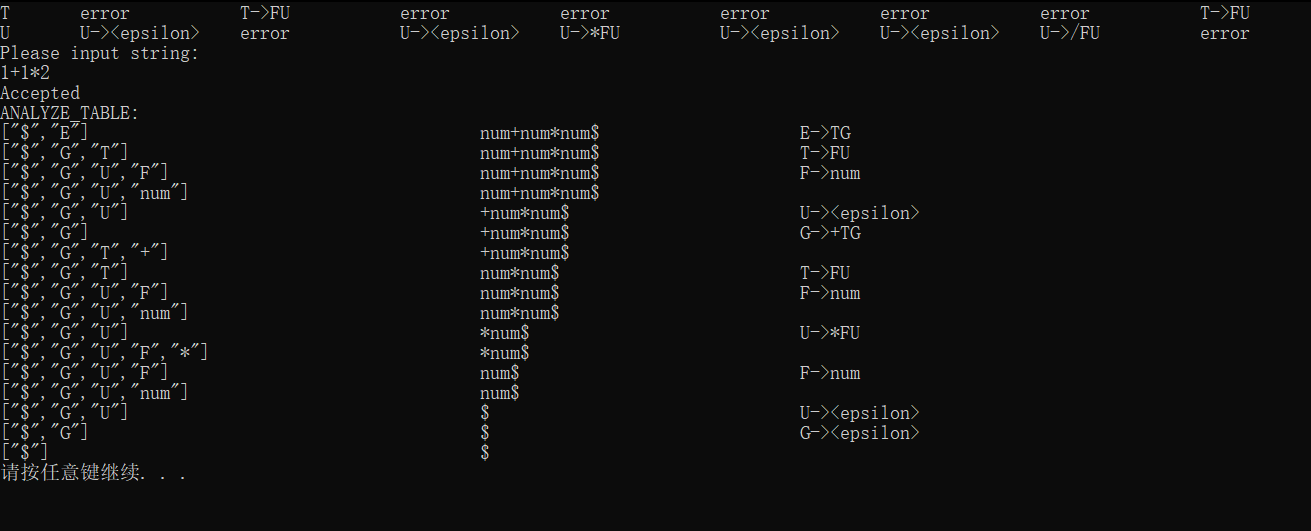
2.2 程序实现

根据所给文法的预测分析表和输入字符串进行非递归预测分析的流程如下

2.2.1 模块设计

在构建预测分析表的过程中我们已经将所有需要使用的模块均定义完毕，所以这里不再需要额外定义；

2.2.2 函数封装

(1)创建非递归预测分析表函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
ANALYZE_TABLE Syntax_Analyzer::create_analyze_table(string input_string, PREDICT_TABLE M)
{
    ANALYZE_TABLE analyze_table;
    int ip = 0;
    input_string += "$";                                                //在输入符号串末尾加上结束符号$
    vector<string> stack;
    stack.push_back("$");                                              //stack用于存放推导过程中符号栈的变化，栈底以$填充
    stack.push_back(M.start_symbol);                                   //栈中填入文法起始符号作为开始标志
    while (stack.size() != 1)
    {
        vector<string> analyze_table_item;
        analyze_table.push_back(analyze_table_item);
        string stack_str = "[\"";
        for (auto iter = stack.begin(); iter != stack.end(); iter++)
        {
            stack_str += *iter + "\",\"";
        }
        stack_str.erase(stack_str.length() - 2, 2);
        stack_str += "]";
        analyze_table.back().push_back(stack_str);
        string input_str = input_string.substr(ip);
        analyze_table.back().push_back(input_str);                     //格式化符号栈analyze_table
        string X = stack.back();                                       //从符号栈stack的第一个符号(栈顶元素)开始比对
        //若栈顶元素等于终结符（find方法如果查找失败会返回end迭代器）
        if (find(M.terminator.begin(), M.terminator.end(), X) != M.terminator.end())
        {
            if (start_pattern(input_string.substr(ip), X))
            {
                ip += X.size();
                stack.pop_back();
            }
            //错误类型：输入符号与栈顶符号不匹配（终结符不匹配）
            else
            {
                error("Error:Input symbol does not match stack top symbol "+X+"!");
                return analyze_table;
            }
        }
        //若栈顶元素等于非终结符
        else if (find(M.nonterminal.begin(), M.nonterminal.end(), X) != M.nonterminal.end())
        {
            string input_string_first;
            if (input_string[ip] == 'i' && input_string[ip + 1] == 'd')
            {
                input_string_first = "id";
            }
            else
            {
                input_string_first = input_string.substr(ip, 1);
            }
            //错误类型：预测分析表中根本就没有相应的产生式或者对应的非终结符
            if (M.table.find(X) == M.table.end() || M.table.find(X)->second.find(input_string_first) == M.table.find(X)->second.end())
            {
                error("Error:There is no corresponding production of "+X+" in the Predict table!");
                return analyze_table;
            }
            string Y = M.table.find(X)->second.find(input_string_first)->second;
            //错误类型：预测分析表中对应的值为error
            if (Y == "error")
            {
                error("Error:The corresponding value of "+X+" in the Predict table is error!");
                return analyze_table;
            }
            else
            {
                stack.pop_back();
                if (Y != "ε")
                {
                    for (auto iter = Y.rbegin(); iter != Y.rend(); iter++)
                    {
                        string first;
                        if (*iter == 'd' && *(iter + 1) == 'i')
                        {
                            first = "id";
                            iter += 1;
                        }
                        else
                        {
                            first = string(1, *iter);
                        }
                        stack.push_back(first);
                    }
                    analyze_table.back().push_back(X + "->" + Y);
                }
                else
                {
                    analyze_table.back().push_back(X + "-><epsilon>");
                }
            }
        }
        //错误类型：栈顶元素既不是终结符也不是非终结符，属于非法符号
        else
        {
            error("Error:The top element of the stack "+X+" is an illegal symbol!");
            return analyze_table;
        }
    }
    if (input_string[ip] == '$')                                        //接受条件是最终输入符号串露出终结符号$(这里不需要再判断符号栈的栈底，因为只有符号栈size为1的时候才能退出while循环)
    {
        cout << "Accepted the Inpute string!" << endl;
        vector<string> analyze_table_item;
        analyze_table.push_back(analyze_table_item);
        analyze_table.back().push_back("[\"$\"]");                     //accepted之后还需要输出最后一行，也就是符号栈为["$"]，输入符号为$
        analyze_table.back().push_back("$");
    }
    //错误类型：不接受，此时符号栈已经为空但输入符号仍不为空
    else
    {
        error("Error:The stack is empty but the input string isn't!");
    }
    cout<<"Analyze table build successfully!"<<endl;
    return analyze_table;
}
(2)输出非递归预测分析表函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void Syntax_Analyzer::print_analyze_table(ANALYZE_TABLE analyze_table)
{
    cout << "\t\t\t\t<====================Analyze table====================>" << endl;
    cout<<"Stack\t\t\t\t\t\tInput String\t\t\tProduction"<<endl;
    for (auto iter = analyze_table.begin(); iter != analyze_table.end(); iter++)
    {
        vector<string> analyze_table_item = *iter;
        for (auto iter2 = analyze_table_item.begin(); iter2 != analyze_table_item.end(); iter2++)
        {
            cout << *iter2;
            if (iter2 == analyze_table_item.begin())
            {
                for (int i = 0; i < 6 - iter2->size() / 8; i++)
                {
                    cout << "\t";
                }
            }
            else
            {
                for (int i = 0; i < 4 - iter2->size() / 8; i++)
                {
                    cout << "\t";
                }
            }
        }
        cout << endl;
    }
}

3.功能验证

首先我们验证对于正确的字符串表达式是否能够成功接收

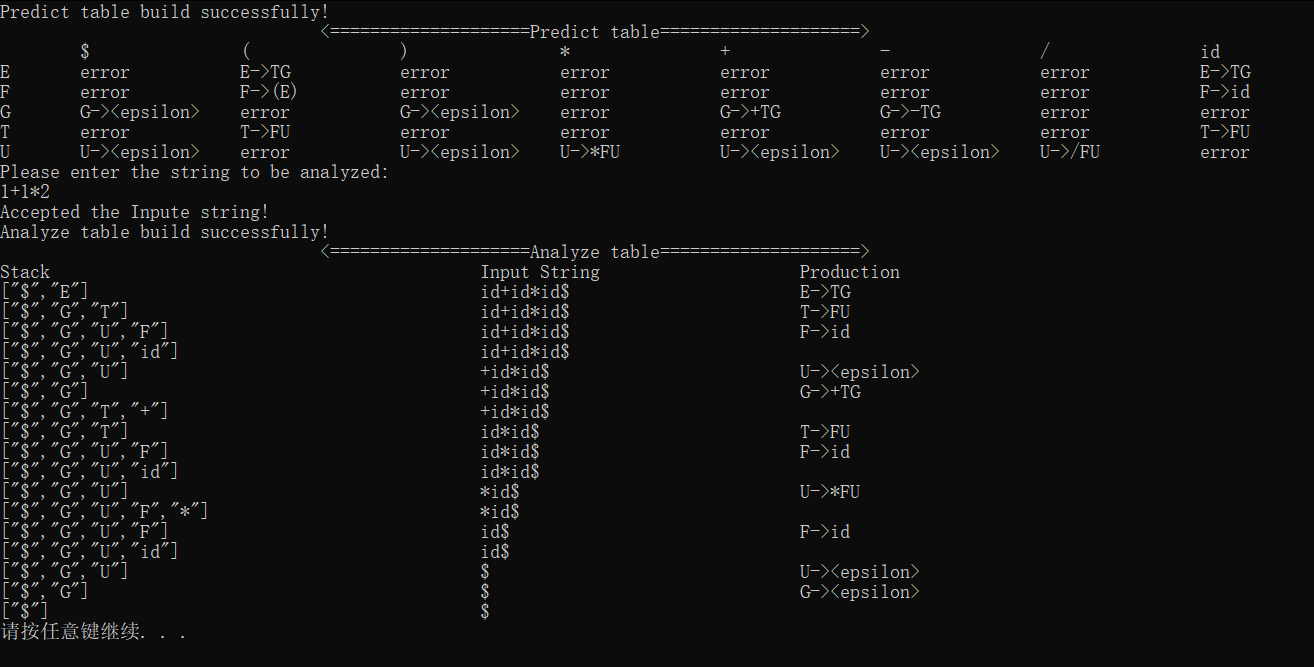
接着验证各种抛出异常的情况，当然并不是所有的异常使用常规方法就可以验证出来的，我们这里给出的都是可以直接输入验证的

预测分析表中对应的值为error

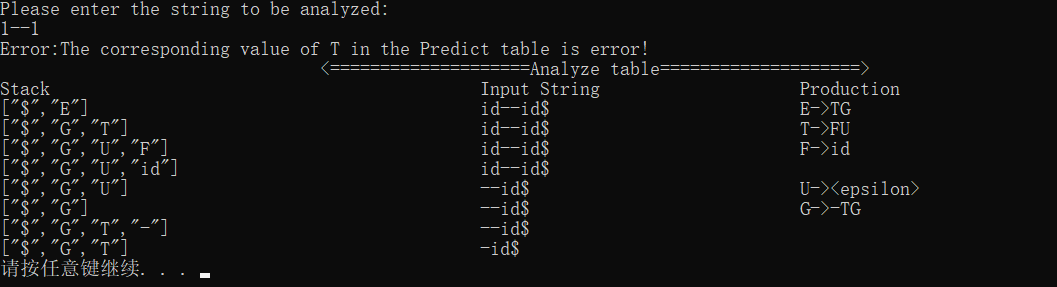
预测分析表中根本就没有相应的产生式

不接受，此时符号栈已经为空但输入符号仍不为空

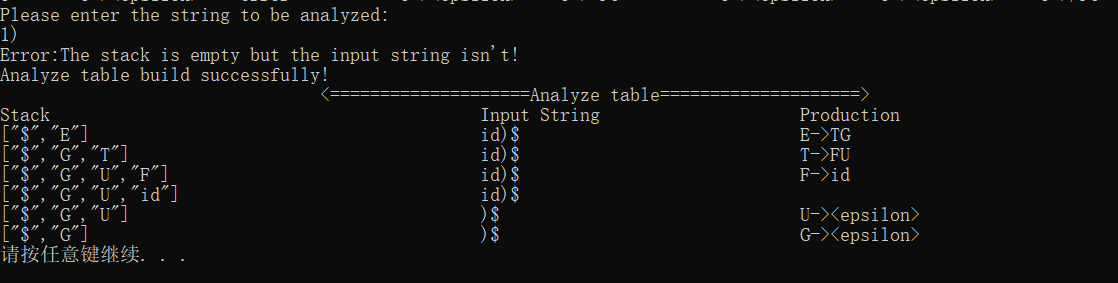
二、自底向上的分析

首先我们得程序输出大致应该是如下形式的

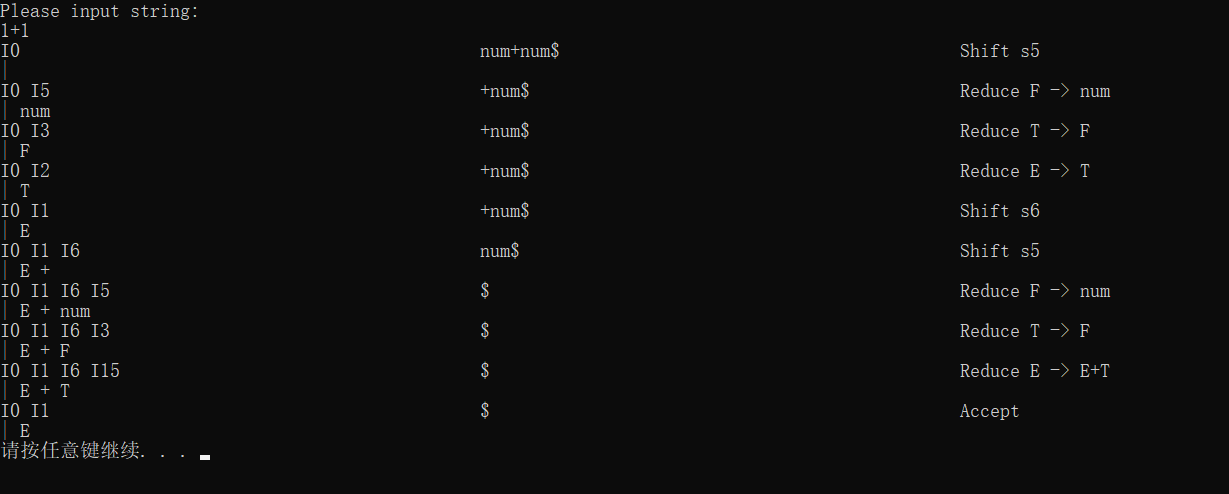
1.基本概念

在进行构造之前我们先回顾必要的概念；

1.1 LR(1)项目

LR(0)的基础上才有SLR(1) —— SLR分析方法只用在分析表上，DFA与LR(0)相同；
LR(1)的基础上才有LALR(1) —— LR(1)的DFA合并同心项才能为LALR(1)；

这四个文法的本质区别实际都只在一点 —— 构造的分析表中ACTION部分的归约动作的区别：

  • LR(0) 状态有归约状态，整个状态都会进行该归约动作；
  • SLR(1) 状态中针对FOLLOW集中有的终结符号会进行该归约动作；
  • LR(1) 状态中针对展望符对应的总结符号进行该归约动作（一般为FOLLOW集的真子集）；
  • LALR(1) 状态中也是针对展望符对应的总结符号进行该归约动作（一般为FOLLOW集的真子集）；

理论上LR(1)的分析效果最好，但是实际开发中LR(1)的状态数会非常多，这是不合理的，所以出现了LALR(1)分析方法（相应的，LALR(1)分析法也存在一些问题）；

在LR(0)分析的时候，我们并没有考虑下一个输入的字符。而对于LR(1)，我们就需要对每一个项目多考虑一项：下一个输入字符（也就是展望符，这是整个LR(1)的难点和核心）

LR(1)项目定义：将一般形式为 [A→α·β, a]的项称为 LR(1) 项；

其中A→αβ 是一个产生式，a 是一个终结符(这里将#视为一个特殊的终结符)，它表示在当前状态下，A后面必须紧跟的终结符，称为该项的展望符(lookahead)

  • LR(1) 中的1指的是项的第二个分量的长度，也就是：往后多看一个字符

  • 形如[A→α·β, a]且β ≠ ε的项中，展望符a没有任何作用（尽管没作用但是构造的过程中仍然要写） —— 当LR(1)中的点号不在项的最右侧，向前看符号没有任何意义；

  • 形如[A→α·, a]的项在只有在下一个输入符号等于a时才可以按照A→α 进行归约：这样的a的集合总是FOLLOW(A)的子集，而且它通常是一个真子集 —— 当点号在最右端时，只有下一个输入的符号和向前看符号一致时，我们才归约这个产生式；

1.2 LR(1)等价项目

有项目 [A->α·Bβ,a]，则该项目的等价项目形式如下 [B->·γ,b]，其中b∈FIRST(βa)；

当β->+ ε时，称b=a叫做继承的后继符，否则称b为自生的后继符；

而仅仅只是利用上述规则还不足以求出所有情况的展望符，我们给出通用求解展望符的算法：

  1. 项目[S’->·S,#]，这个最基本的项目的展望符固定为#
  2. 由项目[A->α·Bβ,a]生成的项目[B->·γ,b]，其中b∈FIRST(βa)
  3. 除了上述自动生成的展望符外，展望符还有两种传播方式：
    • 项目[A->α·Bβ,a]中，β->+ ε时，该项目的a纵向传播到项目[B->·γ,b]
    • 项目[A->α·Bβ,a]中，展望符a无条件横向传播到项目[αB·β,a]

1.3 LR(1)自动机

假设我们有如下文法

构造LR(1)自动机的步骤主要如下：

  1. 拓展文法G得到G’；
  2. 类似LR(0)分析的方法构造得到LR(1)自动机（与LR(0)不同的是多了展望符）

由0)可以推导出I0式，因为I0式中的S是非终结符，所以又可以继续推出等价项目I2和I3。又I2式中圆点后面的L属于非终结符，继续推出I4、I5式【注意：I4、I5中的展望符是=，因为I2式中L后面有终结符=，求展望符就是这么简单】然后继续对左边橙色框中的式子进行相同算法的推导即可；

注：如果除展望符外，两个LR(1)项目集是相同的，则称这两个LR(1)项目集是同心的

1.4 LR(1)分析表

拥有自动机之后就可以得到分析表了，LR(1)与LR(0)分析表类似，只是在归约的某些地方做了更加严格的限制，我们先看一下课堂上讲的LR(1)和SLR(1)分析表的构造方法的对比

根据上述规则，根据上面我们得到的LR(1)自动机可以构造得到下面的LR(1)分析表

2.程序实现

整个LR(1)程序流程分析如下：

  1. 全局初始化，加载LR(1)文法产生式以及对应的LR(1)分析表；（本质上这一步也可以直接使用暴力代入法进行初始化）
    • 加载LR(1)分析表本质上是用于初始化ANALYSE_TABLE；
    • 加载LR(1)产生式本质上是用于初始化SyntaxAnalyzer的产生式；
  2. 调用translate将输入的字符串进行识别，将数字统一转换为id；
  3. 调用SyntaxAnalyzer的分析程序进行分析，若分析成功则输出分析表；

2.1 模块设计

本实验只需要定义如下容器和类：

1
typedef map<string, map<string, string>> PREDICT_TABLE;  //LR语法分析表
1
typedef vector<pair<string, string>> PRODUCTION;         //LR产生式
1
2
3
4
5
6
7
8
class SyntaxAnalyzer{
public:
    void global_init(PREDICT_TABLE M,PRODUCTION P);                                                                                          //全局初始化
    void create_analyze_table(string str,PREDICT_TABLE M,PRODUCTION P);                                         //创建语法分析表，实际就是开始进行LR(1)分析
    void print_analyze_table(vector<string> stack, vector<string> state_stack, string str, string action);  //输出预测分析过程中的分析流程
    int start_pattern(string str, string pattern);                                                             //判断str是否以pattern开头
    string id_translate(string input_string);                                                                           //将数字转换为"id"
};

2.2 函数封装

2.2.1 初始化函数

首先是初始化预测表，传入参数是文件名称，没有输出，将值赋给PREDICT_TABLE

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
void PREDICT_TABLE_init(string file_name)
{
    ifstream file(file_name);
    if (!file.is_open())
    {
        cout << "Error: file " << file_name << " not found" << endl;
        return;
    }
    PREDICT_TABLE table;
    string line;
    vector<string> tokens;
    getline(file, line);
    string word;
    for (int i = 0; i < line.size(); i++)
    {
        if (line[i] == ',' || line[i] == '\n')
        {
            string str2 = "state";
            if (word.size() > 0 && word.compare(str2) != 0)
            {
                tokens.push_back(word);
                //cout<<word<<endl;
                word.clear();
            }
            else
            {
                word.clear();
            }
        }
        else
        {
            word += line[i];
        }
    }
    while (getline(file, line))
    {
        string word;
        int count = 0;
        string state;
        for (int i = 0; i < line.size(); i++)
        {
            if (line[i] == ',')
            {
                if (count == 0)
                {
                    table.insert(make_pair(word, map<string, string>()));
                    state = word;
                    count++;
                }
                else if (word != string("0"))
                {
                    table[state].insert(make_pair(tokens[count - 1], word));
                    count++;
                }
                else
                {
                    count++;
                }
                word.clear();
            }
            else
            {
                word += line[i];
            }
        }
    }
    file.close();
    M = table;
    cout<<"PREDICT_TABLE_init success..."<<endl;
}

然后是初始化产生式函数，只需要将产生式左部和产生式右部的字符串分别传入即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void PRODUCTION_init()
{
    vector<pair<string, string>> formula;
    formula.push_back(make_pair("E","E+T"));
    formula.push_back(make_pair("E","E-T"));
    formula.push_back(make_pair("E","T"));
    formula.push_back(make_pair("T","T*F"));
    formula.push_back(make_pair("T","T/F"));
    formula.push_back(make_pair("T","F"));
    formula.push_back(make_pair("F","(E)"));
    formula.push_back(make_pair("F","num"));
    P = formula;
    cout<<"PRODUCTION_init success..."<<endl;
}

2.2.2 创建预测分析表函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
void SyntaxAnalyzer::create_analyze_table(string str,PREDICT_TABLE M,PRODUCTION P)
{
    cout<<"\t\t\t\t\t\t<=======================Analyze Table======================>"<<endl;
    cout<<"State stack\t\t\t\tSymbol stack\t\t\t\tRemaining string\t\tAction"<<endl;;
    int ip = 0;
    vector<string> state_stack;
    vector<string> stack;
    state_stack.push_back("I0");
    str.push_back('$');
    while (true)
    {
        int ipAdd = 0;
        string state = state_stack.back();
        string a;
        if (start_pattern(str.substr(ip), "num"))
        {
            a = "num";
            ipAdd = 3;
        }
        else
        {
            a = str[ip];
            ipAdd = 1;
        }
        //错误类型：状态Ii并未找到
        if (M.find(state) == M.end())
        {
            cout << "Error: state " << state << " is not found" << endl;
            return;
        }
        //错误类型：某状态对应的token异常(未找到)
        if (M[state].find(a) == M[state].end())
        {
            cout << "Error: Unexpected token " << a << " in state " << state << endl;
            ip += ipAdd;
            continue;
            return;
        }
        string next_state = M[state][a];
        if (start_pattern(next_state, "s") || start_pattern(next_state, "S"))
        {
            print_analyze_table(stack, state_stack, str.substr(ip), "Shift " + next_state);
            stack.push_back(a);
            state_stack.push_back("I" + next_state.substr(1));
            ip += ipAdd;
        }
        else if (start_pattern(next_state, "r"))
        {
            int counti = 0;
            int r = stoi(next_state.substr(1));
            print_analyze_table(stack, state_stack, str.substr(ip), "Reduce " + P[r - 1].first + " -> " + P[r - 1].second);
            for (int i = 0; i < P[r - 1].second.size(); i++)
            {
                if (P[r - 1].second[i] == 'm' && i > 1 && P[r - 1].second[i - 1] == 'u' && P[r - 1].second[i - 2] == 'n')
                {
                    counti -= 2;
                }
                counti++;
            }
            for (int i = 0; i < counti; i++)
            {
                stack.pop_back();
                state_stack.pop_back();
            }
            stack.push_back(P[r - 1].first);
            state_stack.push_back("I" + M[state_stack.back()][P[r - 1].first]);
        }
        else if (next_state == string("acc"))
        {
            print_analyze_table(stack, state_stack, str.substr(ip), "Accept");
            return;
        }
        //错误类型：分析表中没有对应的行为
        else
        {
            cout << "Error: Undefined behavior " << next_state << endl;
            return;
        }
    }
}

2.2.3 输出预测分析表函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void SyntaxAnalyzer::print_analyze_table(vector<string> stack, vector<string> state_stack, string str, string action){
        string ans;
        for (auto i : state_stack)
        {
            ans += i + " ";
        }
        cout << ans;
        for (int i = 0; i < (5 - ans.size() / 8); i++)
        {
            cout << "\t";
        }
        int count_=0;
        for (auto i : stack)
        {
            cout << i << " ";
            count_=count_+1;
        }
        for (int i = 0; i < (5 - count_ / 8); i++)
        {
            cout << "\t";
        }
        cout << str;
        for (int i = 0; i < (4 - str.size() / 8); i++)
        {
            cout << "\t";
        }
        cout << action ;
        cout << endl;
};

3.功能验证

首先我们将文法对应的LR分析表存入对应文件中

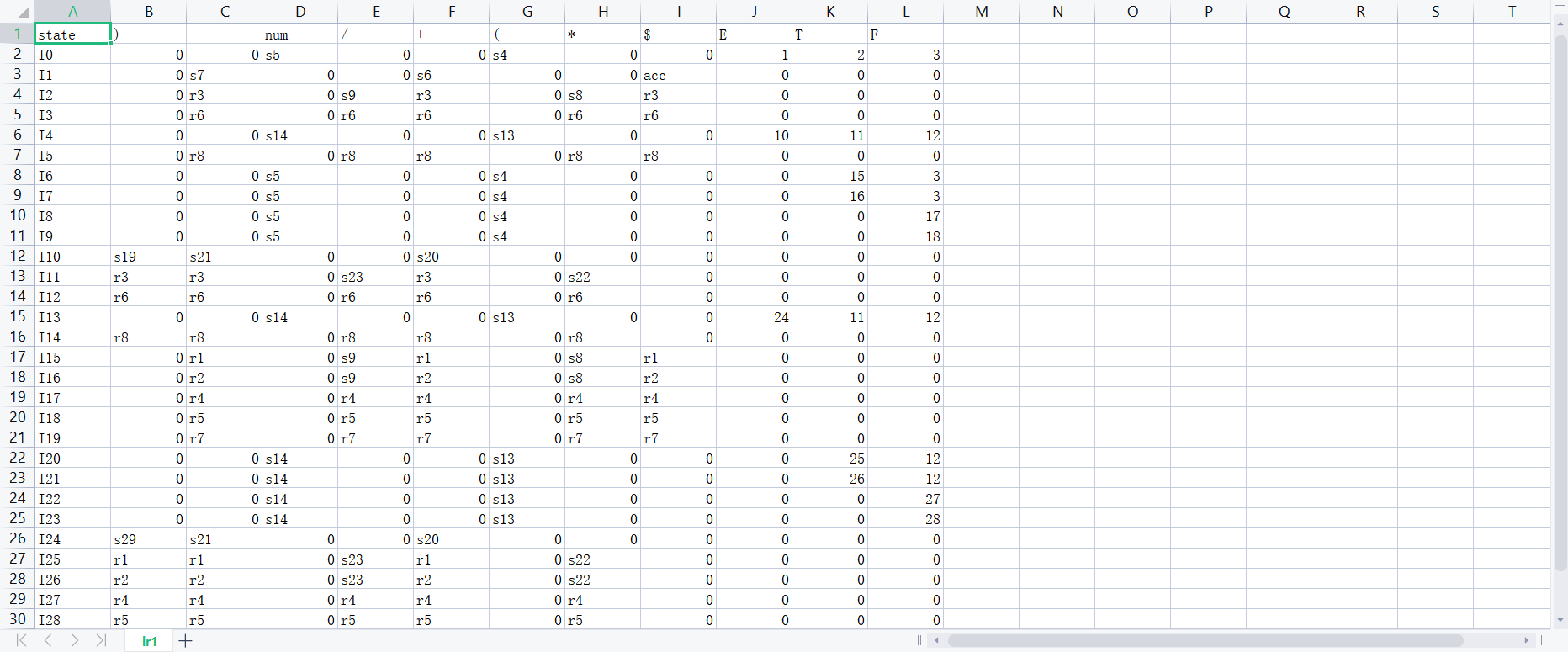
接着我们进行功能测试，首先是正确性测试

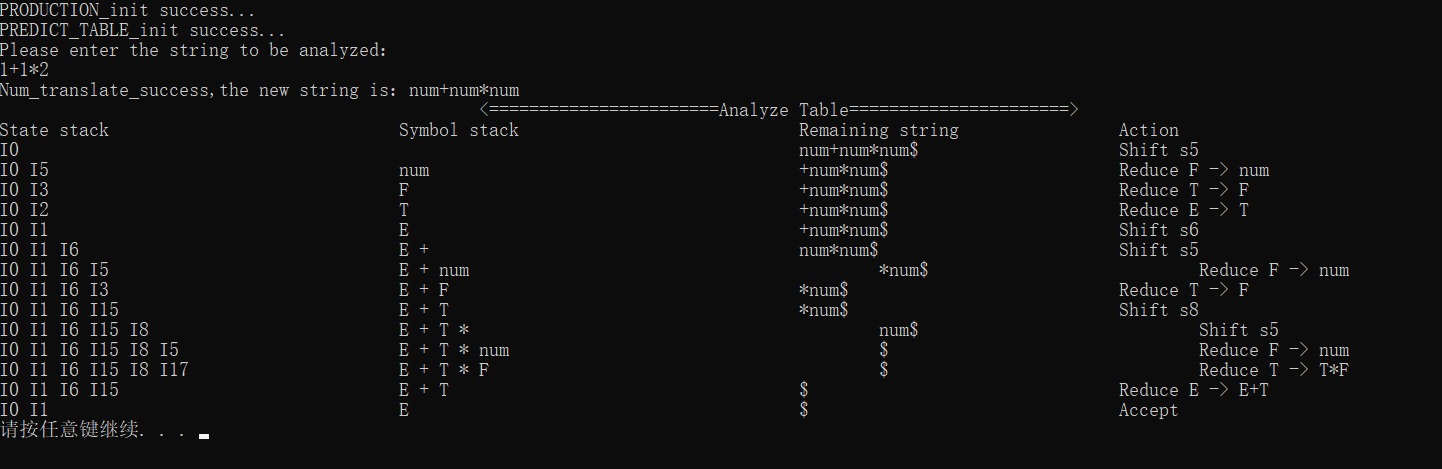
状态对应的token未找到(这里的！不是我们定义的运算符)，处理方法是直接skip接着往后进行分析

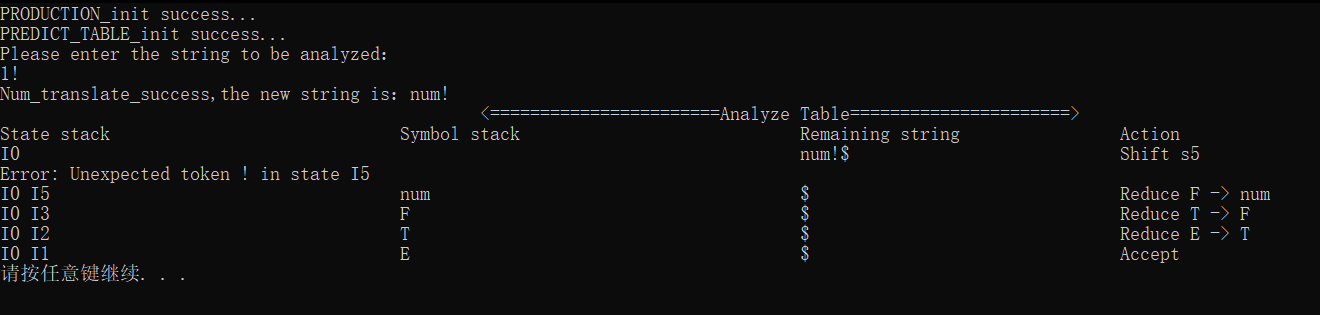
状态不存在，出现这种情况的原因是初始化PREDICT_TABLE的时候出现问题

三、总结

本次实验主要分为三个步骤，根据所给的文法产生式自动构造预测分析表、根据输入字符串和构造的ll(1)预测分析表进行非递归的自上而下的分析、根据所给的输入字符串和所给的lr(1)预测分析表；

难点主要在于对算法的理解和实现上，我们在学习和做题的过程中可能直接套用现成公式所以对于算法的感受并不强烈，但是在实现的过程中深刻的体会到了每一层循环以及每一个需要的数据结构的设计；我们之所以选择使用C++主要也是为了使用其标准库提供的STL库，可以轻松的实现我们需要的诸如栈、映射等结构；在构造预测分析表的过程中，我们要严格掌握first集以及follow集之间的关系，以及如何使用select集构造ll(1)预测分析表，缺点是我们编写的程序只能针对题干所给的文法产生式，拓展性不高，可以考虑在后期抽象函数得到通用的过程；在进行非递归预测分析的过程中需要考虑分析各种可能出现的错误情况并进行错误处理(我们直接选择return并终止预测分析程序)；在进行lr(1)预测分析设计的过程中遇到的最大的问题就是初始化的时候没有设置严格的变量作用域，导致初始化看似完成实际上并没有，所以lr(1)预测分析表实际上是空的，这就导致在后期不管如何修改测试条件都返回的是I0未定义，在经过严格的debug之后发现并解决了这个问题，最后成功的实现了程序；

本次实验带给我最大的感受就是做题和实际开发过程并不完全一致，在将算法实际应用的时候还需要考虑和面对各种各样可能的问题，这也启发我们需要具备缜密的逻辑思维和分析能力。

课程实践
#编译原理
初级项目_语法分析器
https://gintoki-jpg.github.io/2022/11/01/项目_语法分析器/
作者
杨再俨
发布于
2022年11月1日
许可协议