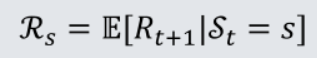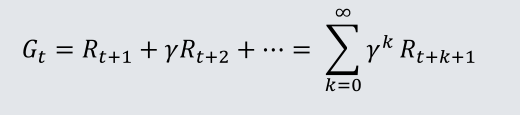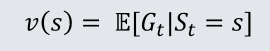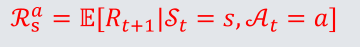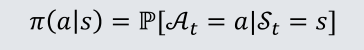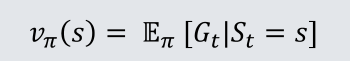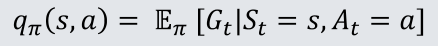强化学习

参考书：RLbook(Sutton、Barto)

参考视频：

参考博客：

2023/2/27 8:59 这门课程还是先啃视频再啃书；

2023/3/2 9:55 强化学习啃书真的效率太低太低了，但是跟着周博磊的教程又显得非常难（后期课程讲的对新手不够友好），现在的想法是在b站直接定向搜索相关知识点，做笔记进行学习 – 这课不需要你花大量时间去学习，只需要布置作业的时候顺便找网课学了然后会做题就行，因为提前学了不做题也是白搭会忘记；

传统人工智能领域的三大学派：

  • 以控制论和强化学习为代表的行为主义学派

    • 20世纪40年代到50年代，行为主义的控制论因其在航空、航天、机械、化工等领域的巨大成功受到了极大重视但其应用往往不被认为是一种“智能”，因而长期独立发展，游离于人工智能研究者的视野之外；

  • 以逻辑推断和贝叶斯学习为代表的符号主义学派

    • 20世纪50年代人工智能的概念被正式提出以后，符号主义的数理逻辑以及贝叶斯学习等经典机器学习理论一直一枝独秀，引领着人工智能的研究和应用，尤其是专家系统、知识工程和经典机器学习理论的大量成功应用，使得它成为20世纪在人工智能研究中占据统治地位的主流学派；

  • 以神经网络为代表的联结主义学派

    • 20世纪 60 年代类脑模型的研究和80年代反向传播算法的提出都使得神经网络的研究在短时间内出现过热潮，然而理论局限和应用瓶颈一次又一次地把神经网络的研究打入冷宫，直到21世纪初，深度学习理论被提出，借助GPU等计算机硬件的算力飞跃并与大数据结合，迅速产生了巨大的产业技术红利，使得联结主义一跃成为当前人工智能研究最炙手可热的学派；

以联结主义的神经网络为代表的深度学习毫无疑问是 21 世纪初人工智能领域的最重要、最具实用意义的技术突破之一，越来越多的研究者把深度学习的改良性研究视为工业界的应用技巧，而开始关注与联结主义的经典深度学习不同的人工智能范式探索，不同学派的思想融合产生了两个重要趋势

  • 一个是将联结主义与符号主义融合起来，将神经网络的“黑箱学习”与先验知识、符号推理和经典机器学习结合，实现可解释、可推理、可操控的新一代“白箱学习”；
  • 一个则是将联结主义与行为主义融合起来，将基于静态数据和标签的、数据产生与模型优化相互独立的“开环学习”，转变为与环境动态交互的、在线试错的、数据（监督信号）产生与模型优化紧密耦合在一起的“闭环学习”；
    • 强化学习就是“闭环学习”范式的典型代表，它与传统的预先收集或构造好数据及标签的有监督学习有着本质的区别，它强调在与环境的交互中获取反映真实目标达成度的反馈信号，强调模型的试错学习和序列决策行为的动态和长期效应

一、强化学习介绍

学习的本质：人类通过与环境交互来学习，在交互中学习几乎是所有学习和智能理论的基本思想；

相比于其他机器学习方法，强化学习更加侧重于以交互目标为导向进行学习，关于其他机器学习的方法参考机器学习 - Tintoki_blog (gintoki-jpg.github.io)；

在机器学习的所有不同形式中，强化学习是和人类以及其他动物最接近的一种学习方式，并且它的许多核心算法最初也受到生物学习系统的启发；

1.强化学习概念

强化学习最显著的两个特征：试错和延迟收益；

  • 强化学习问题的定义：

    • 在智能体为了实现目标而不断与环境产生交互的过程中，抓住智能体所面对的真实问题的主要方面 – 感知；

    • 具备学习能力的智能体必须能够在某种程度上感知环境的状态，然后采取动作并影响环境状态 – 动作；

    • 智能体必须同时拥有和环境状态相关的一个或多个明确的目标 – 目标；

  • 强化学习方法的定义：一种对目标导向的学习与决策问题进行理解和自动化处理的计算方法；

  • 强化学习和有监督学习的区别：

    • 有监督学习是从外部监督者提供的带标注训练集中进行学习。每一个样本都是关于情境和标注的描述（标注，即针对当前情境，系统应该做出的正确动作，也可将其看作对当前情景进行分类的所属类别标签）；

    • 采用有监督学习是为了让系统能够具备推断或泛化能力，能够响应不同的情境并做出正确的动作，哪怕这个情境并没有在训练集合中出现过；

    • 有监督学习并不适用于从交互中学习这类问题，在交互问题中，我们不可能获得在所有情境下既正确又有代表性的动作示例。在一个未知领域，若想做到最好（收益最大），智能体必须要能够从自身的经验中学习；

  • 强化学习和无监督学习的区别：

    • 无监督学习是一个典型的寻找未标注数据中隐含结构的过程；
    • 强化学习的目的是最大化收益信号而不是找出数据的隐含结构；
    • 认为强化学习是与有监督学习和无监督学习并列的第三种机器学习范式；

  • 强化学习的挑战 – “试探”与“开发”的折中权衡

    • 智能体必须开发已有的经验来获取收益，同时也要进行试探，使得未来可以获得更好的动作选择空间；
    • 无论是试探还是开发，都不能在完全没有失败的情况下进行；
    • 就目前而言，在有监督学习和无监督学习中，至少在最简单的形式中，并不存在权衡试探和开发的问题；

强化学习的另一个关健特征 – 整体性

强化学习明确地考虑了目标导向的智能体与不确定的环境交互这整个问题，而很多其他方法都仅仅只关注孤立的子问题，而忽视了子问题在更大情境下的适用性；

强化学习则从一个完整的、交互式的、目标导向的智能体出发，所有强化学习的智能体都有一个明确的目标，即能够感知环境的各个方面，并可以选择动作来影响它们所处的环境；

上面提到的完整的、交互式的、目标导向的智能体并不一定是完整的有机体或机器人，它们也可以是一个更大的动作系统的组成部分；

2.强化学习特征

所有的强化学习的问题都涉及一个活跃的决策智能体和环境之间的交互作用

– 强化学习强调在与环境交互的过程中学习，在这个不确定的环境中，智能体想要实现一个目标，智能体的动作会影响未来环境的状态，进而影响未来的决策和机会，因此正确的选择需要考虑到间接的、延迟的动作后果，需要有远见和规划；

强化学习问题中，无法完全预测动作的影响，因此智能体必须频繁地监视其环境并做出适当的反应

– 所有的问题都涉及明确的目标，智能体可以根据这个目标来判断进展；

强化学习有明确的且标，并且正确的动作需要规划和预测，这样才能考虑每次选择的长期影响

Q：是什么使得强化学习不同于其他机器学习算法？

A：

  • 没有监督数据，只有奖励（reward）信号
  • 奖励信号不一定是实时的，可能存在延迟
  • 时间是一个重要因素
  • 智能体（Agent）当前的动作（Action）影响后续接收到的数据

3.强化学习要素

除了智能体和环境之外，强化学习系统有四个核心要素：策略、收益信号、价值函数以及对环境建立的模型（可选）：

  • 智能体和环境

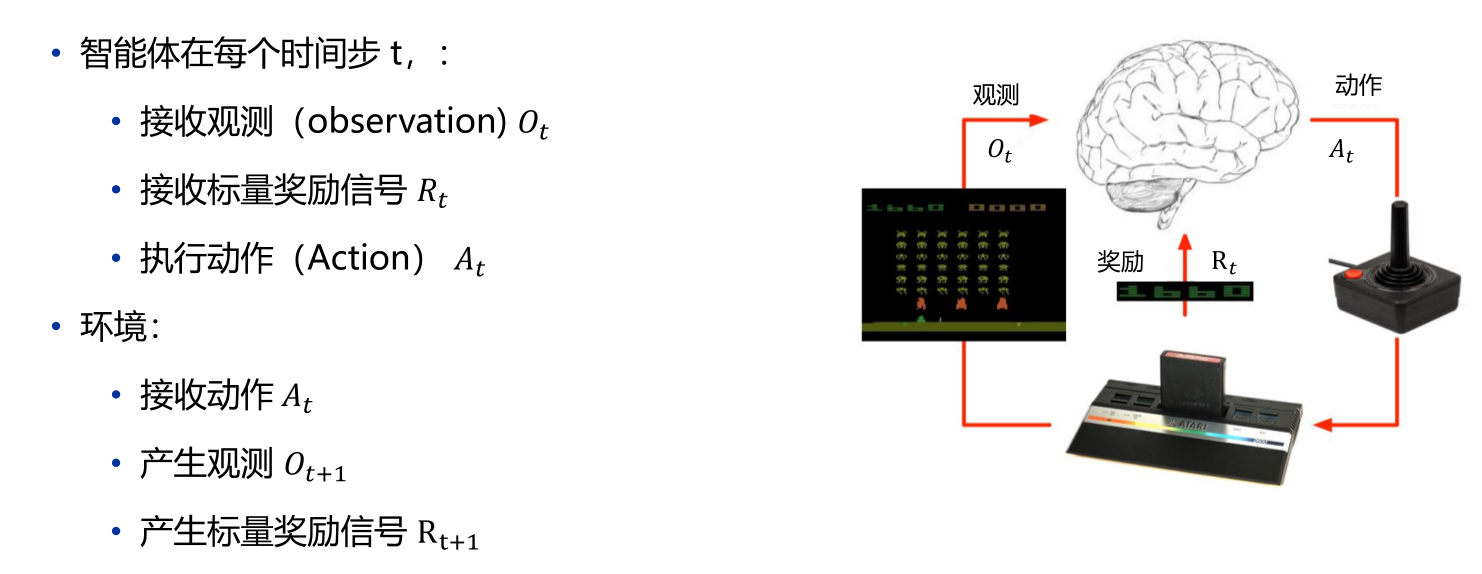
  • 策略（序列决策）
    • 策略定义了学习智能体在特定时间的行为方式。简单地说，策略是环境状态到动作的映射。策略本身是可以决定行为的，因此策略是强化学习智能体的核心。一般来说，策略可能是环境所在状态和智能体所采取的动作的随机函数。
  • 收益信号（短期奖励）
    • 收益信号定义了强化学习问题中的目标。在每一步中，环境向强化学习智能体发送一个称为收益的标量数值。智能体的唯一目标是最大化长期总收益。因此，收益信号是改变策略的主要基础。一般来说，收益信号可能是环境状态和在此基础上所采取的动作的随机函数。
  • 价值函数（长期奖励）
    • 收益信号表明了在短时间内什么是好的，而价值函数则表示了从长远的角度看什么是好的。简单地说，一个状态的价值是一个智能体从这个状态开始，对将来累积的总收益的期望。尽管收益决定了环境状态直接、即时、内在的吸引力，但价值表示了接下来所有可能状态的长期期望。
    • 在制定和评估策略时，我们最关心的是价值。动作选择是基于对价值的判断做出的。我们寻求能带来最高价值而不是最高收益的状态的动作，因为这些动作从长远来看会为我们带来最大的累积收益。
    • 确定价值要比确定收益难得多。收益基本上是由环境直接给予的，但是价值必须综合评估，并根据智能体在整个过程中观察到的收益序列重新估计。
  • 环境的模型（可选）
    • 这是一种对环境的反应模式的模拟，或者更一般地说，它允许对外部环境的行为进行推断。例如，给定一个状态和动作，模型就可以预测外部环境的下一个状态和下一个收益。
    • 环境模型会被用于做规划。规划，就是在真正经历之前，先考虑未来可能发生的各种情境从而预先决定采取何种动作。
    • 使用环境模型和规划来解决强化学习问题的方法被称为有模型的方法。而简单的无模型的方法则是直接地试错，这与有目标地进行规划恰好相反。

4.强化学习局限性

强化学习十分依赖“状态”这个概念，它既作为策略和价值函数的输入，又同时作为模型的输入与输出；

一般可以把状态看作传递给智能体的一种信号，这种信号告诉智能体“当前环境如何”，即当前智能体可知的环境信息；

状态产生自一些预处理系统，这些系统从逻辑上说是智能体周边环境的一部分；

强化学习方法的适用范围

  • 一些优化方法不必须显示地计算价值函数 – 这些方法采取大量静态策略，每个策略在扩展过的较长时间内与环境的一个独立实例进行交互。这些方法选择获取了最多收益的策略及其变种来产生下一代的策略，然后继续循环更新，这类方法称为进化方法；
    • 如果策略空间充分小，或者可以很好地结构化以找到好的策略，或者我们有充分的时间来搜索，那么进化方法是有效的；
    • 进化方法在那些智能体不能精确感知环境状态的问题上具有优势；
    • 进化方法并不是一种在与环境互动中学习的一类方法，进化方法忽视了强化学习问题中的一些有用结构：它们忽略了所求策略是状态到动作的函数这一事实；也没有注意个体在生命周期中都经历过哪些状态，采取了哪些动作。尽管在一些情形下，这些信息容易引起误导（例如当状态被错误感知时），但是在更多的情形下，这些信息可以让搜索更高效；

Q：强化学习方法和进化方法究竟有什么不同？可以举例吗？

A：用井字棋的例子

  • 进化方法每一次策略的改变都基于很多次博弈，只有每局比赛最后的结果会被考虑，而在博弈中间发生的事情将会被忽略。例如，如果玩家获胜，就会认为这次游戏中所有的动作都有功劳，而与每一步具体动作有多关键无关，这些功劳甚至会被分配给那些从未出现的动作；

  • 基于价值函数的方法允许我们对单个状态进行评估；

  • 进化方法和价值函数方法都是对策略空间进行搜索，但是学习价值函数的过程利用了博弈过程中的可用信息；

5.强化学习分类

基于策略的更新与学习方法，强化学习方法可分为：

  • 基于价值函数
  • 基于直接策略搜索
  • 基于执行者-评论者（Actor-Critic）

根据强化学习算法是否依赖模型，强化学习方法可分为：

  • 基于模型的强化学习算法
  • 无模型的强化学习算法

根据环境返回的回报函数是否已知，强化学习方法可分为：

  • 正向强化学习算法
  • 逆向强化学习算法：从专家的示例中学习回报函数。

二、有限马尔可夫决策过程

本章重点：马尔可夫决策过程、贝尔曼期望方程、贝尔曼最优方程

马尔可夫决策过程(Markov decision processes)也称MDP，为什么要学习MDP？主要有以下几点原因：

  • MDP是强化学习问题在数学上的理想化形式
  • MDP中的环境是完全可观测的
  • 几乎所有的强化学习问题都可以在数学上表示为马尔可夫决策过程（即使是部分可观测也可以近似表示为MDP）

因此，可以说MDP是整个强化学习的基础

1.马尔可夫过程

1.1 马尔可夫性质

定义：状态St具有马尔可夫性，当且仅当P[St+1|St]= P[St+1|S1,…,St]

简单来说，马尔可夫性质就是“未来只与现在有关，与过去无关”，即只需要当前状态就可以推测未来的信息（当前状态是对过去信息的充分统计），马尔可夫性质可以将问题简化

1.2 状态转移矩阵

  • 对于马尔可夫状态s与其后继状态s’，它们的状态转移概率定义为

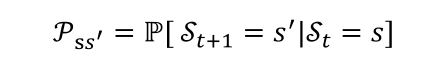
状态转移概率

  • 状态转移矩阵P定义了马尔可夫状态s到其所有后继状态s’的状态转移概率（矩阵的每一行总和为1）

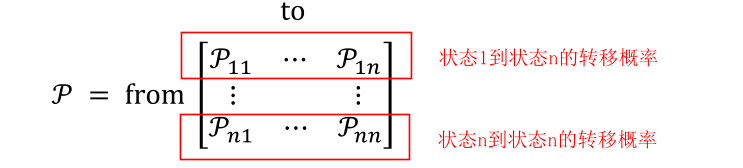
状态转移矩阵

1.3 马尔可夫过程

特征：马尔可夫过程是一种无记忆的随机过程，只看当下不考虑过去，极大简化了需要考虑的问题

马尔可夫过程可以分为三类：

  • 时间、状态都离散的马尔科夫过程（马尔科夫链）
  • 时间连续、状态离散的马尔可夫过程（连续时间的马尔科夫链）
  • 时间、状态都连续的马尔可夫过程

定义：马尔可夫过程由元组(S,P)构成

  • S是有限状态的集合
  • P是状态s到其所有后继状态s’的状态转移矩阵

下图是一个简单的马尔可夫过程

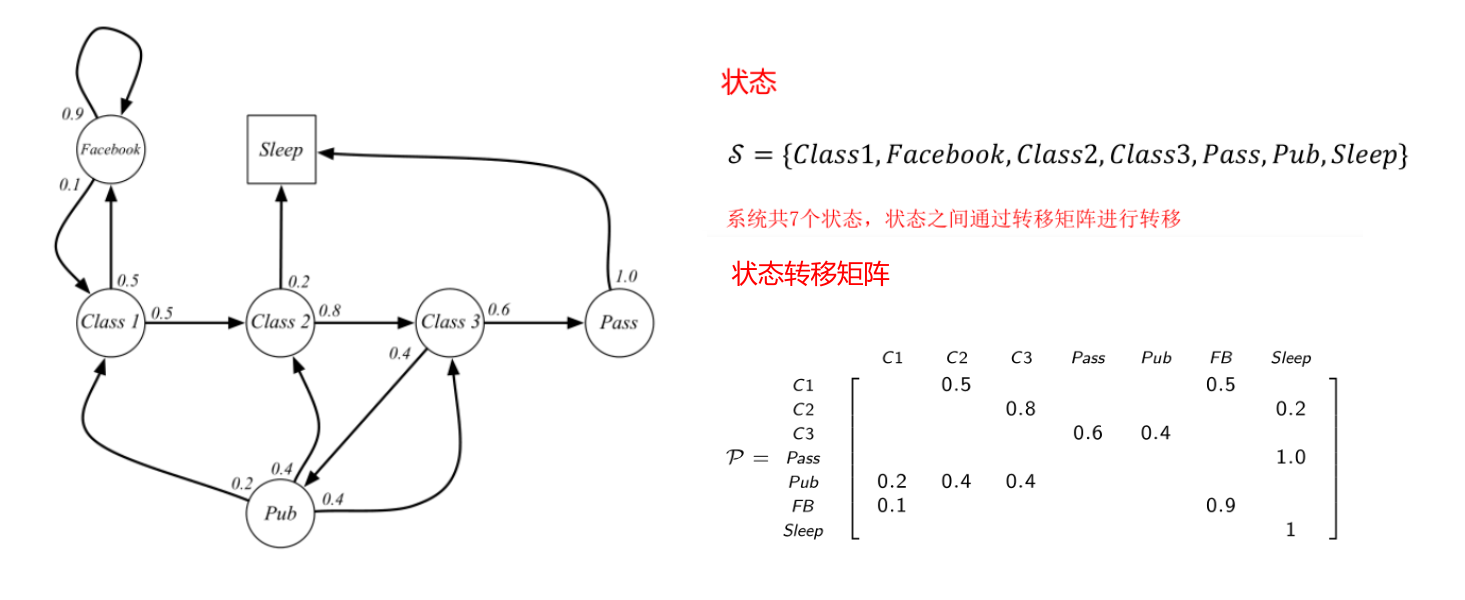
马尔可夫过程

1.4 分幕

从马尔可夫过程中随机采样的一些子序列，这每个子序列就称为分幕(Episodes)；

例如我们从初始状态C1开始，到终止状态sleep结束，采样得到的一些子序列（使用的是上面的马尔可夫过程的图）

分幕

2.马尔可夫奖励过程

特点：马尔可夫奖励过程是具有价值的马尔可夫过程

定义：马尔可夫奖励过程由元组(S,P,Rs,γ)构成

  • S是有限状态的集合
  • P是状态s到其所有后继状态s’的状态转移矩阵
  • Rs是奖励函数，是到达状态s时系统所给奖励的期望值
  • γ是折扣因子

2.1 奖励函数

定义：到达状态s时系统所给奖励的期望值

奖励

  • 到达状态s时，系统所给奖励可能每次都不同，奖励函数中的期望值去除了系统所给奖励的随机性（期望反映随机变量平均取值的大小，可以去除某些随机因素）；
  • 奖励函数常常记为Rs=E[Rt+1|St=s]，之所以将状态s对应的奖励记为Rt+1是因为系统赋予奖励是下个阶段的事情；
  • 当我们将奖励函数记为R而不是Rs时表示该系统在赋予奖励的时候不需要求期望（即该过程不存在随机性）；

2.2 折扣因子

折扣因子的取值范围为[0,1]，主要有以下作用：

  • 避免有环的马尔可夫过程计算收益时出现无限循环（当到达一定的衰减程度后，后面的值可以直接忽略）

  • 从金融投资回报的角度讲，即时奖励（immediate rewards）比延时奖励（delayed rewards）更吸引人

  • 动物/人类行为中都表现出对即时奖励的偏好

  • 可以表达未来的不确定性

当γ=0表示只看眼前的收益，不用考虑未来的收益；当γ=1表示当前收益和未来收益相同，表现不是特别考虑当前收益； – 折扣因子的选择和真实问题相关，具体问题具体分析

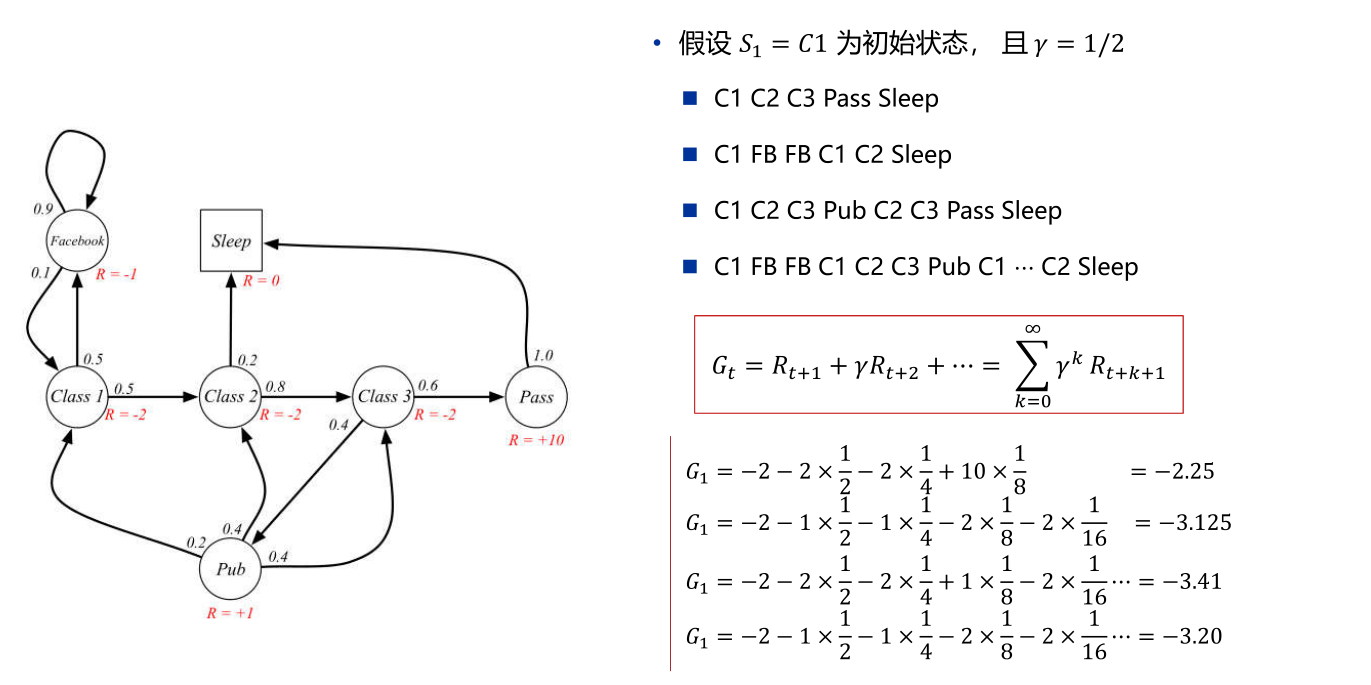
2.2.1 回报

定义：在一个马尔可夫奖励过程中，从t时刻的状态St开始直到终止状态，所有奖励的衰减求和Gt称为回报

回报

回报可以理解为回合制游戏中完成一回合的总分，与衰减因子γ有关，衰减因子可以衰减未来的奖励；

例子-回报计算

2.2.2 价值函数

  • 价值函数v(s)给出了状态s的长期价值
  • 价值函数的输入为某个状态，输出为该状态的长期价值

定义：在马尔可夫奖励过程中，一个状态的期望回报被称为该状态的价值函数

价值

状态的回报是针对每一个幕而言，对整个马尔可夫奖励过程来说，选择哪一个幕具有不确定性，故对所有回报求期望平均 – 平均分才是最优的评判标准；

回报的期望去除了状态转移之间的随机性以及系统赋予状态奖励的随机性

2.3 贝尔曼方程

贝尔曼方程可以求解价值函数，贝尔曼方程本质上是一个递推式

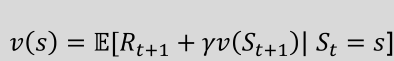
贝尔曼方程_1

贝尔曼方程表示当前状态的价值等于当前状态的系统奖励和下一个时刻到达的状态的价值衰减后累加求和的结果的期望 – 将价值函数拆分为即时奖励Rt+1和后继状态的折扣值γv(St+1)

贝尔曼方程的推导过程如下，因为期望的期望实际上等同于一个期望，故标红的两个式子是等价的

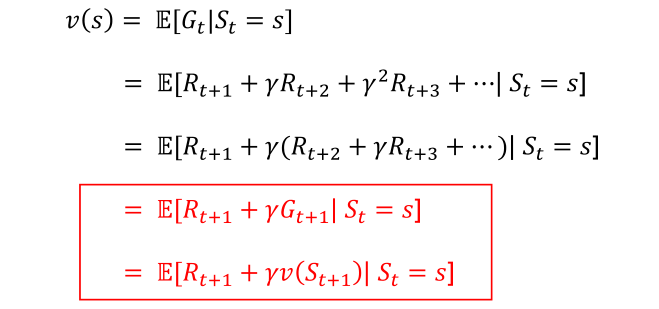
然而上面那种贝尔曼方程并不是最终可以用于计算价值的形式，如果用s’表示s状态的下一时刻任一可能的后继状态，则贝尔曼方程可表示为

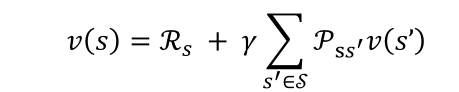
贝尔曼方程_2

其中

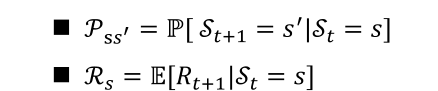
若衰减因子为1，我们使用贝尔曼方程来计算下面状态的价值

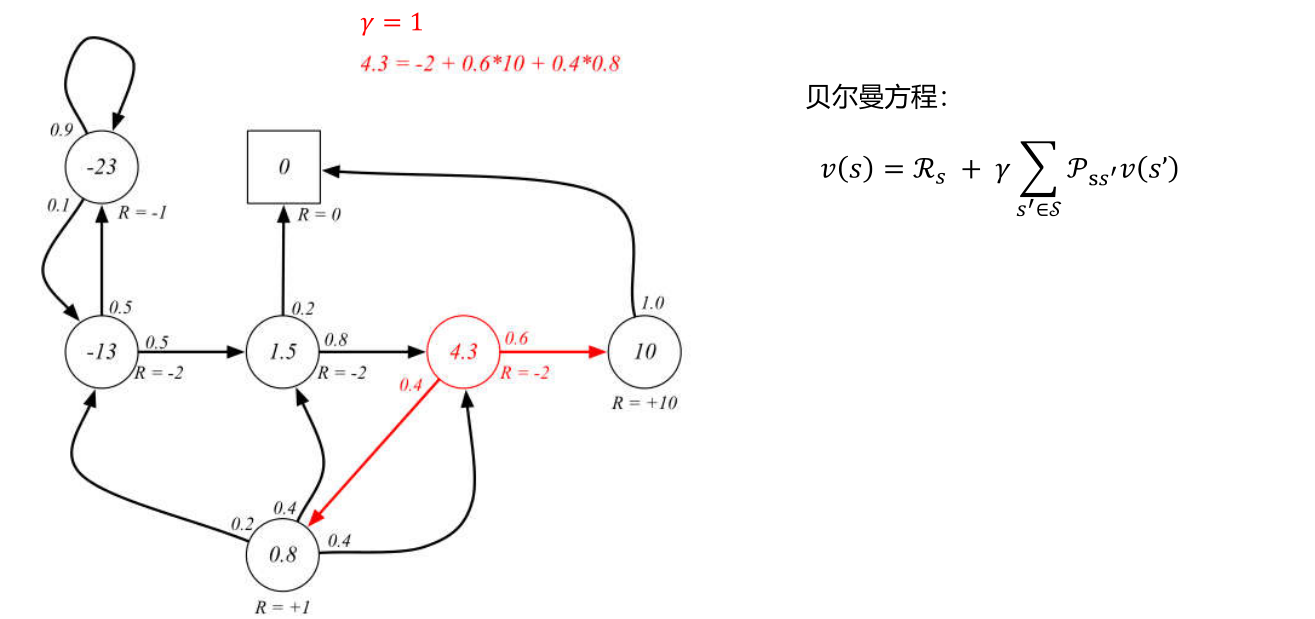
例子-价值计算

初始时所有的状态对应的价值函数都是随机初始化的，不断通过贝尔曼方程更新价值函数，在迭代过程中有两种不同的更新方式，一种是一次性将所有新的V(s)替换掉旧值，即同步更新，另一种是异步更新，也就是每次计算出V(s)后就立刻进行geng’xin

贝尔曼方程用矩阵表示则有第三种表现形式

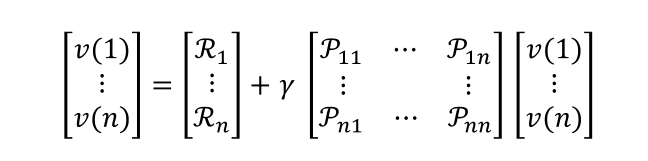
贝尔曼方程_3

这种表现形式下的贝尔曼方程可以直接求解

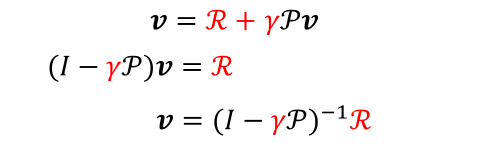
当然这种直接求解的方式在有|S|个状态的时候计算复杂度为O(|S|^3^)，仅适用于小型的马尔可夫奖励过程，对于大型的MRP可以使用其他迭代的方法解决如动态规划、蒙特卡洛评估、时序差分学习…

3.马尔可夫决策过程

马尔可夫决策过程（MDP）是具有决策的马尔可夫奖励过程（MRP）其所有状态满足马尔可夫性质

定义：马尔可夫决策过程由元组(S,A,P,R,γ)

  • S是有限状态的集合
  • A是有限动作集合
  • P是状态s到其所有后继状态s’的状态转移矩阵，其中的每一个状态转移概率形式为
  • Rs是奖励函数，是到达状态s时系统所给奖励的期望值，奖励函数的形式为
  • γ是折扣因子

上述定义表示了在马尔可夫决策过程中，智能体的动作可以干预系统的随机性结果，下图是一个典型的马尔可夫决策过程

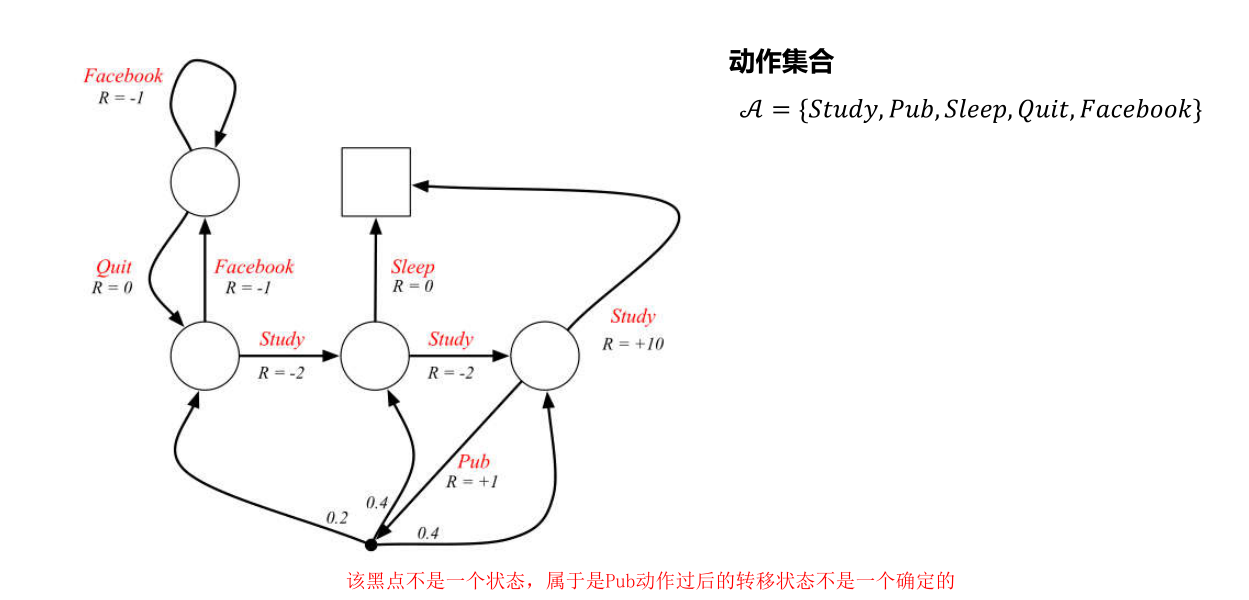
马尔可夫决策过程

3.1 策略

定义：策略Π是一个函数，输入为状态s，输出为采取动作α的概率

策略

  • 策略完全定义了智能体的行为；

  • 马尔可夫决策过程中，策略仅取决于当前状态s（而不是历史记录）；

3.2 价值函数

3.2.1 状态价值函数

状态价值函数用于区分不同的策略Π（高手和低手）

定义：MDP中，一个状态价值函数vΠ(s)是指从状态s出发，遵循策略Π得到的期望回报

状态价值函数

3.2.2 动作价值函数

动作价值函数用于区分同一个策略的不同策略

定义：MDP中，一个动作价值函数qΠ(s,α)是指从状态s开始，遵循策略Π，对当前状态s执行动作α得到的期望回报

3.3 贝尔曼期望方程

前面贝尔曼方程中已经介绍过，状态价值函数可以分解为 即时奖励+后继状态的折扣值

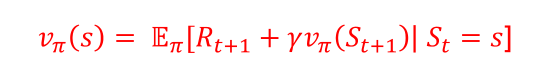
相应的动作价值函数可以进行类似的分解

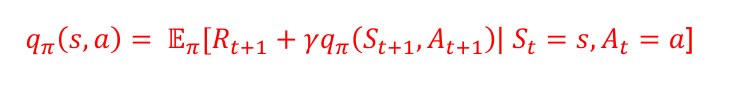
利用回溯图和上述分解结果可以推导得到状态价值函数和动作价值函数之间的转换式

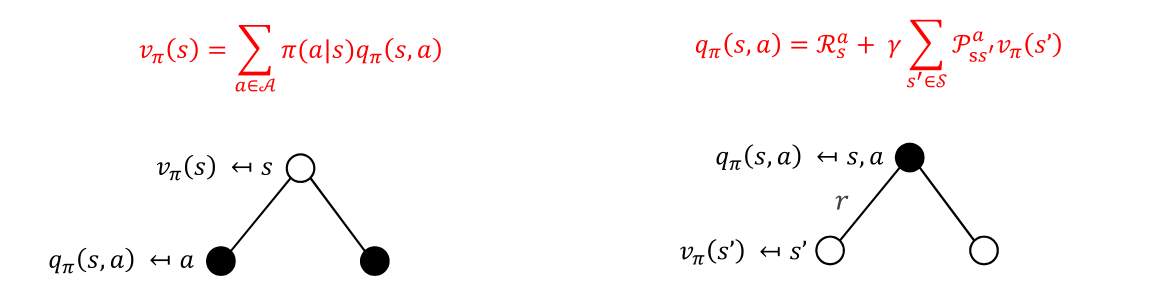
状态价值函数和动作价值函数转换式

有了上述转换式，我们可以代入原本的式子得到贝尔曼期望方程（状态价值函数的递推式和动作价值函数的递推式）

贝尔曼期望方程

3.4 最优价值函数

最优价值函数明确了MDP的最优可能表现，一旦最优价值函数知晓，则认为MDP已完成求解

  • 最优状态价值函数是所有策略产生的状态价值函数中，使状态s价值最大的函数：
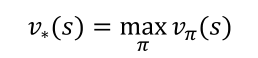
  • 最优动作价值函数是指所有策略产生的动作价值函数中，使状态-行为<s,a>对价值最大的函数：

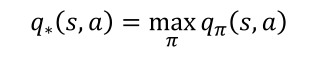
3.5 最优策略

策略偏序：当且仅当对任意状态s都有vΠ(s)>=vΠ’(s)，记为策略Π>=Π’

最优策略：在有限状态和动作的MDP中，一定存在一个最优策略遵守策略偏序，不劣于其他所有的策略

  • 所有的最优策略具有相同的最优状态价值函数vΠ*(s)=v*(s)
  • 所有的最优策略有相同的动作价值函数qΠ*(s,a)=q*(s,a)

即最优策略可能在系统中有很多个，但最优状态价值函数和最优动作价值函数只有一个；

可以通过最大化动作价值函数来找到最优策略（这是一种贪婪策略），如果我们知道最优动作价值函数则立刻可以获得最优策略

最优策略

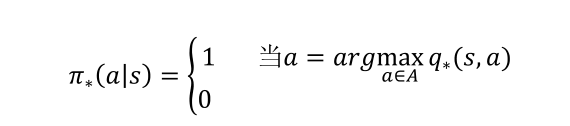
3.6 贝尔曼最优方程

目的：建立最优策略、最优动作价值函数、最优状态价值函数的关联

贝尔曼最优方程通过贝尔曼期望方程代入最优策略得到

贝尔曼期望方程

最优策略

贝尔曼最优方程_1

贝尔曼最优方程_2

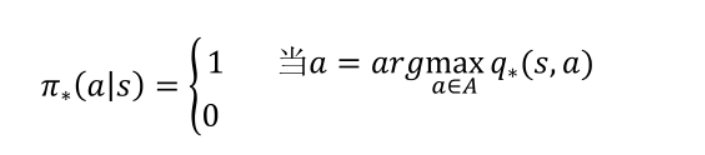
因为贝尔曼最优方程不是线性的，所以不能使用与策略优化相同的直接矩阵解决方案，只能通过一些迭代法解决（价值迭代、策略迭代、Q学习、Sarsa…）

三、动态规划

本章重点：策略评估、策略改进、策略迭代、价值迭代

动态规划是一类优化算法，将待求解的目标将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到目标问题的解，动态规划的核心特点：

  • 最优子结构 – 子问题的最优解是可以得到的
  • 重复子问题 – 子问题的解决方案可以存储和重用

（上述动态规划定义与算法的动态规划定义是相同的，实际上强化学习的DP思想和算法中的DP思想的确很类似）

Q：为什么要在强化学习中学习DP？

A：

  • 在完备的马尔可夫决策过程中（完备表示系统的奖励Rs和状态转移矩阵完全知道），DP可用于计算得到最优策略；
  • 尽管完备的环境模型只是一个假设且传统的DP计算复杂度高，但是DP为其他方法提供了基础，所以有必要学习DP在强化学习中的运用；

在强化学习中使用DP求解最优策略，主要有两种方式：

  • 策略迭代：使用贝尔曼期望方程，求解最优策略，包含两个核心步骤：
    • 策略评估 – 输入MDP（S，A，P，R，γ）和策略π，输出价值函数vπ
    • 策略提升 – 输入MDP（S，A，P，R，γ）和价值函数vπ，输出最优价值函数v*，和最优策略π*
  • 价值迭代：使用贝尔曼最优方程，求解最优策略

价值迭代是策略迭代的特殊情况，效率稍高

1.策略迭代

1.1 策略评估

策略评估顾名思义就是评估谁的策略Π更好，经过前面的学习知道可以将该问题转化，即预测一个给定的策略Π在所有状态s下的价值函数vΠ；

如何求出给定策略Π在所有状态s下的价值函数呢？ – 迭代使用贝尔曼期望方程进行回溯，用初始价值函数迭代更新后继价值函数，直到算法收敛到vΠ，因此该方法也称为迭代策略评估

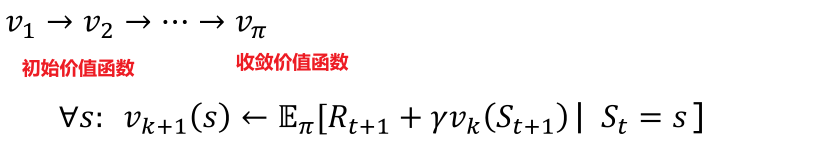
迭代贝尔曼期望方程

下面给出迭代策略评估的算法

  • 系统任意初始化得到的V(s)并不是该策略Π真正的价值函数，因为并不满足贝尔曼期望方程，只有整个系统收敛时得到的价值函数才会满足贝尔曼期望方程；
  • 系统收敛得到的vΠ一定满足贝尔曼期望方程，但是不一定满足最优方程，因为只有最优策略的vΠ才满足贝尔曼最优方程；

1.2 策略提升

前面介绍了如何预测一个给定策略Π在所有状态s下的价值函数vΠ，是否可以根据该价值函数来改进该策略得到策略Π’，使得策略Π’的价值函数高于策略Π的价值函数？

这里我们应用贪婪方法来改进策略Π，具体使用的是当时最大化动作价值函数寻找最优策略的方式（实际上就是调整策略Π在状态s下对应的动作a的概率）

最优策略

PS：此处的*应该改为Π，表示普通策略的最大化动作价值函数

1.3 策略迭代

在大部分问题中，需要进行多次的策略评估和策略改进的迭代才能得到该问题的最优策略

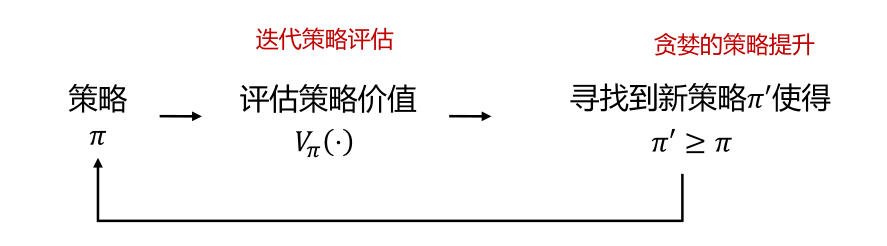
下面给出完整的策略迭代算法

由以上算法得到的最优策略Π，是满足贝尔曼最优方程的，也是满足系统收敛条件的，此时，对于所有的状态s对应的状态价值函数都是最优状态价值函数；

2.价值迭代

在策略迭代的策略评估过程中，我们并不需要迭代到k=∞即系统收敛时才进行策略提升，当策略评估迭代的次数k越小表示运算量越小，当k=1时，此时的策略迭代就成了价值迭代

在价值迭代中，因为只需要进行一次策略评估

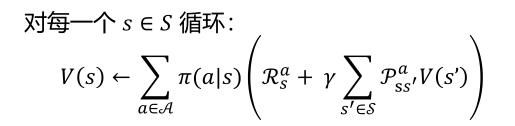
而在策略提升中会使用最大化动作价值函数

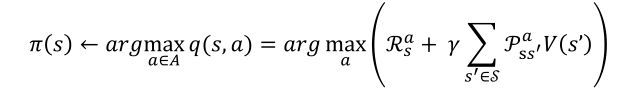
将这两个函数合并可以得到这样一个公式（也就是将策略迭代中的策略评估和策略提升两个步骤合二为一）

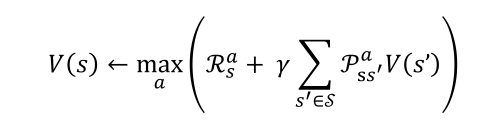
这个公式实际上就是贝尔曼最优方程

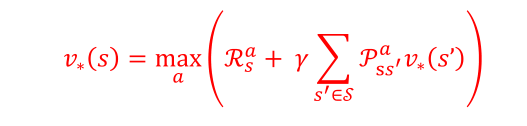
满足贝尔曼最优方程的策略一定是最优策略，这也不难解释为什么可以通过价值迭代找到最优策略；

迭代使用贝尔曼最优方程进行回溯得到的最优策略Π，可能完全是一个全新的策略，因为在迭代过程中得到的价值函数可能不符合任何一个已知策略 – 价值迭代并不是在已知策略上进行改进，而是直接基于价值寻找一个最优策略；

下面给出价值迭代算法

四、无模型预测

本章重点：蒙特卡洛预测、时序差分预测

上节课学习了用动态规划来进行规划，以解决一个已知的MDP（已知表示已知表示状态之间的转移概率和在某个状态下得分的期望都已知），但实际上生活中很多问题并不是已知的MDP，也就是我们所说的无模型问题，这节课将介绍三种无模型强化学习方法，这三种方法的目的同动态规划相同都是用于评估一个策略的好坏，区别就是一个是在已知的MDP下，一个是在无模型的MDP下；

1.蒙特卡罗学习

蒙特卡罗学强化学习简称MC，主要有以下特点：

  • MC方法可直接从分幕（episodes）的经验中学习；
  • MC是无模型算法：无需了解MDP转换和奖励机制，即与状态转移矩阵和奖励概率没有关系，仅看已经发生过的状态和已经得到的奖励；
  • MC需要从完整的幕中学习：有些问题是不能结束的（如沙盒游戏，即没有分幕、没有回合），这是不适用MC方法的；
  • MC的基本思想：价值=平均回报，即蒙特卡洛的基本思想就是用大量数据取平均值去逼近真实值；

前面介绍的DP中的回报定义为

MC和DP关于回报的定义并没有区别，区别在于MC对于价值函数的定义：

  • DP中状态的期望回报被称为该状态的价值函数，MC中的状态的平均回报被称为该状态的价值函数；
  • 平均数是一个统计学概念，期望数是一个概率论概念，前者是实际观察得到的统计量，后者是理论上的理想值；
  • MC策略基于大数定律：在试验不变的条件下重复试验多次，随机事件的频率近似等于它的概率；

1.1 MC策略评估

MC策略评估的目的与DP策略评估目的相同，都是计算策略Π下状态s对应的价值函数，主要有两种评估方式：

  • 首次访问型：
  • 每次访问型：

PS：

  • 之后我们都默认使用的MC策略评估是每次访问型；
  • 无论是上述哪种策略评估方式，其中的V(s)都不是真正的状态s的价值函数，只有当N(s)足够大时利用大数定律（实际就是系统收敛时）得到的V(s)才是真正的价值函数；

1.2 累进式MC策略评估

上面更新平均回报的方式比较直接，即需要记录状态s发生的次数和每次状态s发生时对应的回报，我们思考是否能对上述式子进行改进；

用数学公式表示每次访问型计算平均回报（将每次状态s发生的Gt求和与状态s发生的次数作除法）

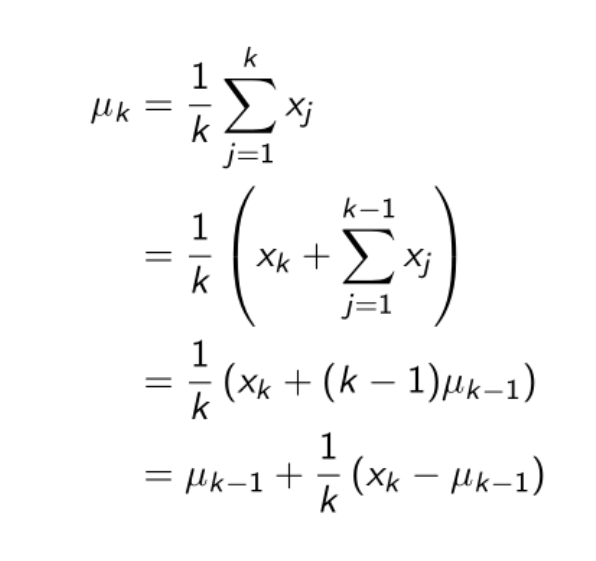
将上述式子整理过后得到一个式子，其中uk-1是上一次的平均回报，xk是这次的回报，k是截止此时状态s一共发生了多少次，这个式子表明我们不需要再将前面每一次状态s发生的次数和回报都记录下来，只需要借助状态s发生的次数k以及上一次计算出的平均回报就可以更新本次的平均回报（也就是价值函数）

类比上述累进式均值更新的思想改写原MC的策略评估式子可以得到累进式MC策略评估式

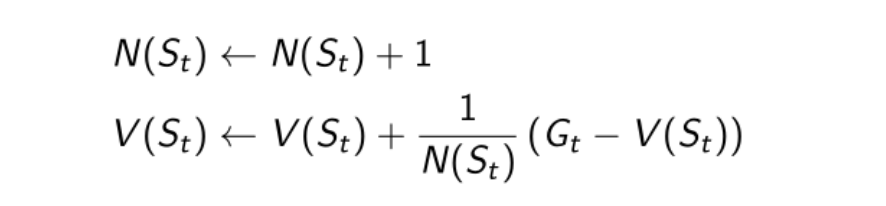
在非平稳问题中，跟踪连续平均值（即忘掉旧episodes）可能很有用

非平稳问题表示这整个环境系统本身也在发生改变，在这样的环境中不需要记录很久之前的信息，所以使用α参数代替N计数，使α参数逐渐衰减即让系统只记住最近发生的信息，这样有利于系统的收敛

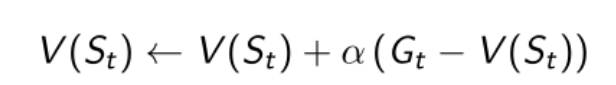
上式就是最终的MC策略评估式，即迭代使用MC方法计算状态s的价值函数的公式（这意味着我们初始的V(St)并不是状态s真正的价值函数，需要迭代直至系统收敛此时才是真正的价值函数）；

2.时序差分学习

时序差分学习基于这样一个事实，即状态s的价值函数可以写为如下两种形式

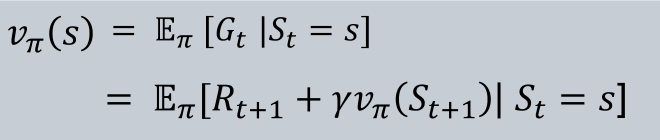
MC最大的特点就是需要等待“游戏”结束，而某些游戏是不会结束的（沙盒游戏），此时可以使用时序差分强化学习，TD主要有以下特点

  • TD方法可直接从经验中学习：意味着不需要模型，即不需要了解状态转移矩阵和奖励概率；
  • TD同样是无模型的；
  • TD通过自举从不完整的幕中学习（简单来说自举就是使用猜测的结果去更新猜测）：不完整的幕表示只需要幕中的子序列即可学习；

2.1 TD策略评估

前面已经介绍过MC的策略评估函数如下

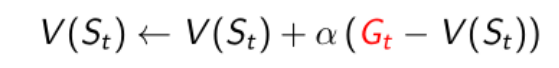
即MC使用实际的回报Gt来更新价值V(St)，而时序差分学习TD(0)使用的是估计的回报来更新价值

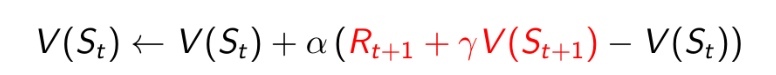
上述式子中的Rt+1+γV(St+1)称为TD target，Rt+1+γV(St+1)-V(St)称为TD error；

为什么说TD是使用不确定的回报来更新价值呢？因为公式中的Rt+1和St+1(下一个将要转移到的状态)具有随机性，即只需要知道现在状态对应的奖励Rt+1以及下一步将要转移到哪个状态St+1就可以对上述式子进行更新，如何知道当前状态对应的奖励和下一步转移到哪个状态呢？ – 自举（简单来说就是猜）

2.2 MC和TD

2.2.1 学习环境

TD可以在知道最终结果之前学习

  • TD可以在每一步之后在线学习
  • MC必须等到episode结束才能知道回报

TD可以在没有最终结果的情况下学习

  • TD可以从不完整的序列中学习
  • MC只能从完整序列中学习
  • TD在连续（非终止）环境中工作
  • MC仅适用于episode（终止）环境

2.2.2 方差&偏差

MC具有高方差，零偏差

  • 良好的收敛性
  • 对初始值不太敏感
  • 很容易理解和使用

TD方差低，但存在偏差

  • 通常比MC更高效

  • TD(0)收敛至vπ(St)：上一次的价值函数是否靠谱会影响这一次的预测

  • 对初始值更敏感

2.2.3 马尔科夫性

TD利用了马尔科夫性

  • 通常在马尔可夫环境中效率更高

MC没有利用马尔科夫性

  • 通常在非马尔可夫环境中更有效

2.2.4 离线&在线

简单理解在线学习和离线学习：在线是打一轮评估一轮，可以认为幕无限；离线是指将所有的幕放在那里评估，认为幕有限；

前面讨论的都是在线学习，即幕无限的情况，根据大数定律可以知道V(s)最终会收敛到vΠ(s)，但是如果是幕有限的情况（离线学习），应当如何进行学习呢？

对MC来说就重复的使用这k个幕就行，对于TD来说采样不同长度的幕的子序列即可；

2.2.5 小结

下面这张图从深度优先和广度优先的角度将MC、DP和TD做对比

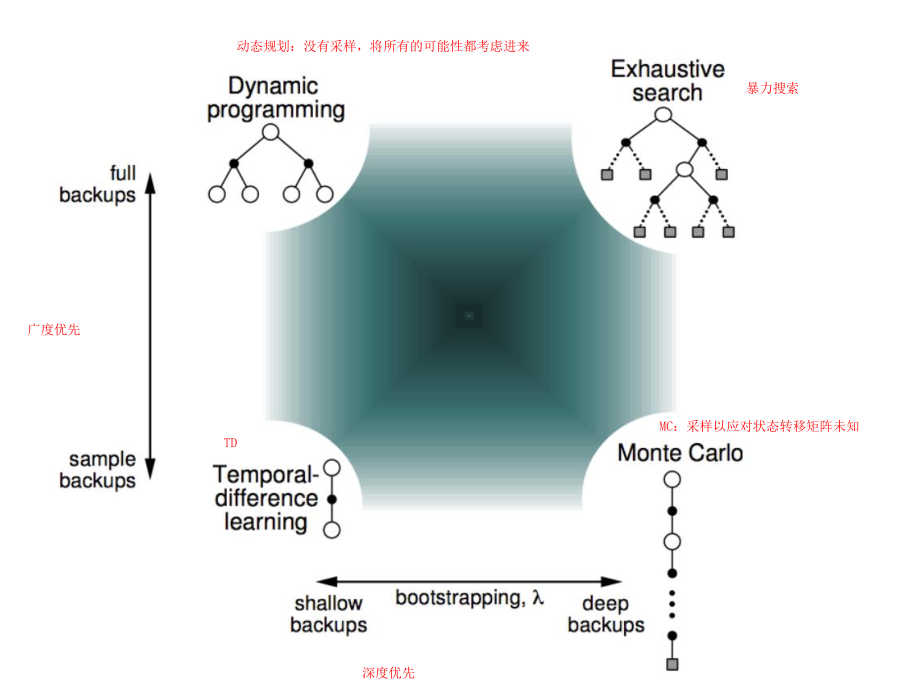
3.TD(λ)

前面对比MC和TD的时候说到，MC具有高方差、低偏差，TD具有低方差、高偏差；

TD(0)并未考虑任何接下来的状态，也就是直接根据本身的状态进行猜测，而MC是考虑了所有的一幕中的状态，所以能够准确的进行计算，如果让TD向后考虑几个状态（即TD已知之后的几个状态），能否改善其性质？下面的式子表示TD考虑了其后n步的回报的表达式

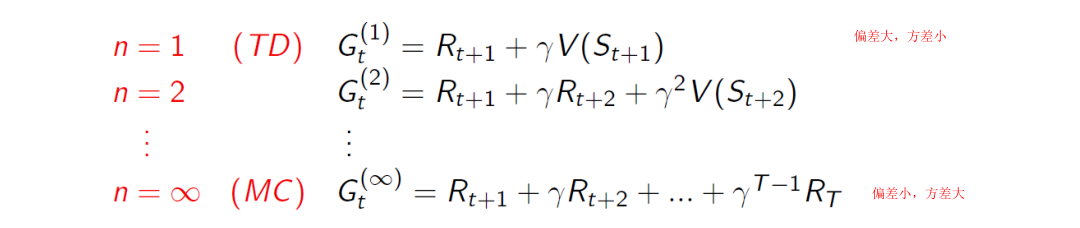
从上式可以看出，n的大小决定了偏差和方差的大小，一种简单的想法就是将不同的n的值平均，但是这种平均效果不好，考虑对不同的n附加不同的权值改变其影响大小

加权融合

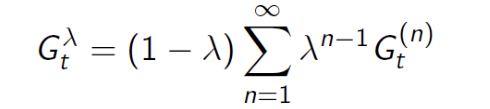
加权融合，将每步的Gt乘以一个权重((1-λ)λ^n-1^)再进行累加，最终融合的结果G^λ^t既考虑了方差也考虑偏差，一般来说越往后其权重越小（最后一步除外）

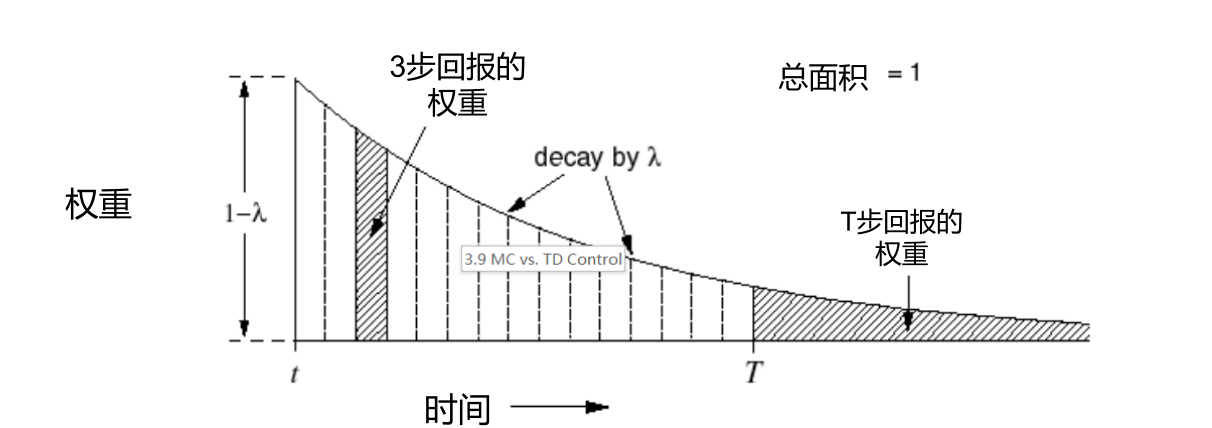
将上式中的G^λ^t代入价值函数计算公式有

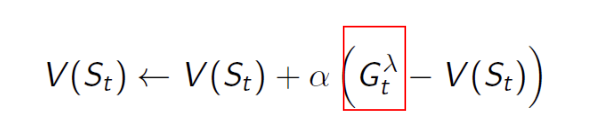
这就是TD(λ)的策略评估公式

五、无模型控制

本章重点：MC控制，TD控制SARSA与Q-learning

上一节介绍的是无模型预测方法，即如何估计一个未知MDP的价值函数，本节课介绍无模型控制方法，即如何优化一个未知MDP的价值函数（实际上这一章因为优化方法的不同会导致评估的对象随之改变）；

在开始本章之前需要先区分两个概念：

  • 在轨学习：理解为自己作为玩家和观察者，边打游戏边升级策略
  • 离轨学习：理解为自己作为观察者观察玩家打游戏，升级自己的策略

1.在轨MC控制

前面DP中介绍过策略迭代主要分为策略评估和策略提升，如下图

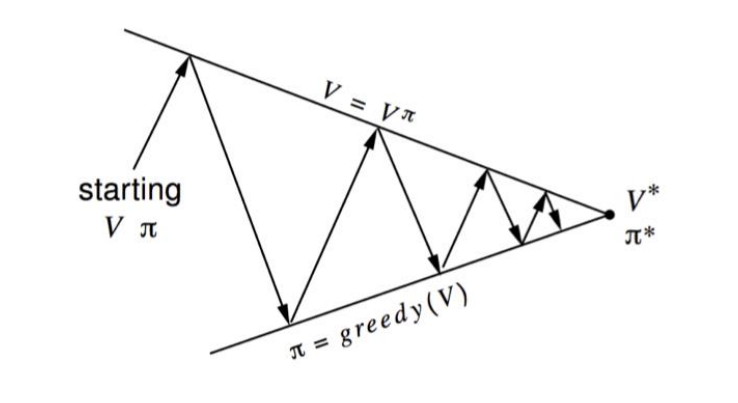
但是在DP的策略迭代算法中无论是策略评估还是策略改进都涉及状态转移矩阵P^a^SS’，而在无模型的条件下状态转移矩阵是未知的，所以不能直接使用DP中的策略迭代算法；

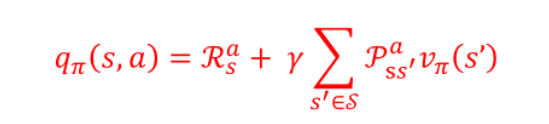
状态价值函数和动作价值函数之间的转换

简单来说就是对于V(s)进行贪婪策略优化需要MDP模型（即状态转移矩阵）

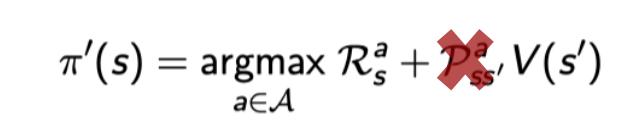
但是针对动作价值函数Q(s,a)进行贪婪策略优化是无模型的（这点很好理解，因为没有状态转移矩阵所以无法建立动作价值函数和状态价值函数之间的关系，那么就直接计算动作价值函数而跳过状态价值函数）

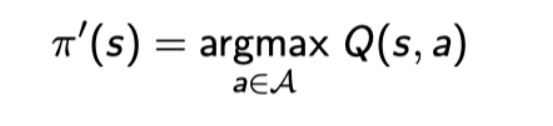
Q：有人可能会好奇为什么这里突然出现了动作价值函数？以及为什么会使用到状态转移矩阵？

A：策略优化，就是在优化该策略中某些状态s对应的动作a；而使用的贪婪优化策略就是当策略对应的动作价值函数最大时将该策略赋值为1，否则为0；因为对于策略Π来说有多个状态，所以需要将这些状态的动作都考虑进去，这就需要使用到状态转移矩阵；

1.1 MC控制

基于上述对MC进行策略迭代遇到问题的讨论，这里我们不使用状态价值函数进行策略迭代，而使用动作价值函数进行迭代，如下图

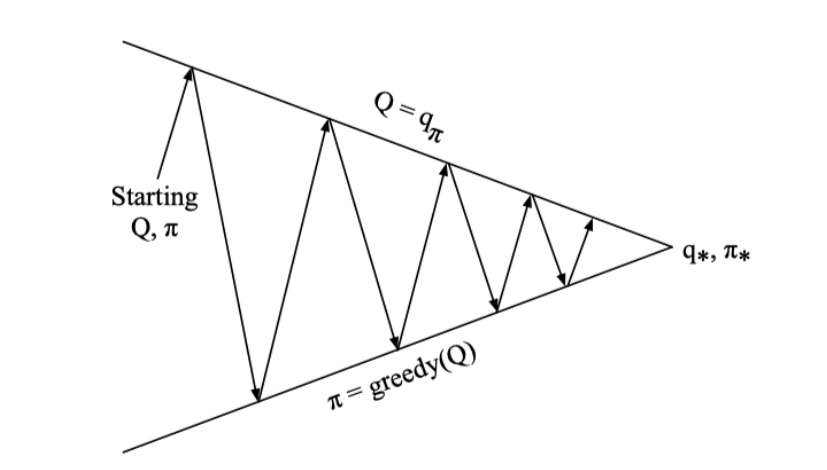
这意味着在进行策略评估的时候评估的是动作价值函数，进行策略优化的时候优化的也是动作价值函数；

首先定义MC中的动作价值函数，同[MC策略评估](#1.1 MC策略评估)中定义状态价值函数类似

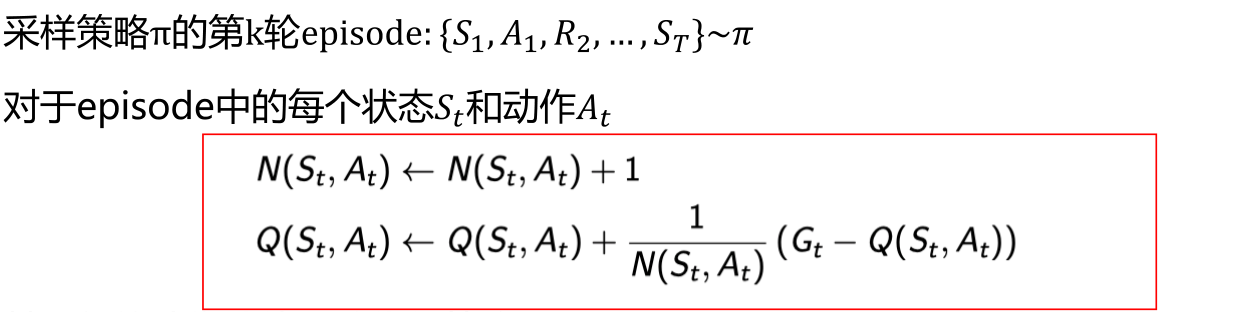
接着需要定义MC的策略优化，在DP中无需考虑探索和利用的问题，这是因为DP将所有的可能性都考虑进去（即所有的路线都被点亮）

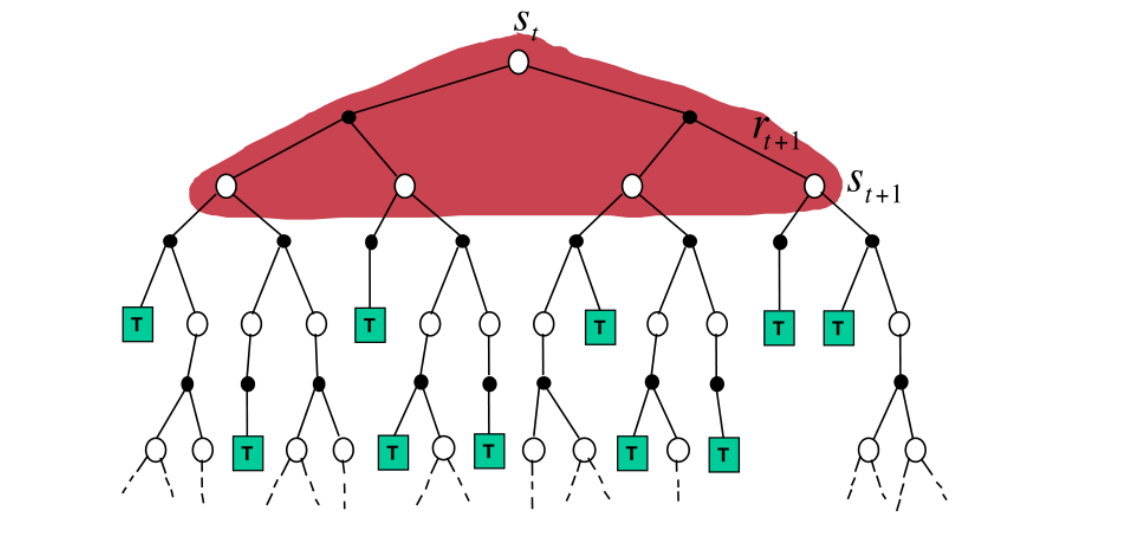
为了避免一味的“利用”而错过某些可能收益更高的“探索”，我们对原有的贪婪策略附加一些探索因子，即对于m个动作来说，有1-ε的概率选择贪婪动作（即利用），有ε的概率选择随机动作（即探索）

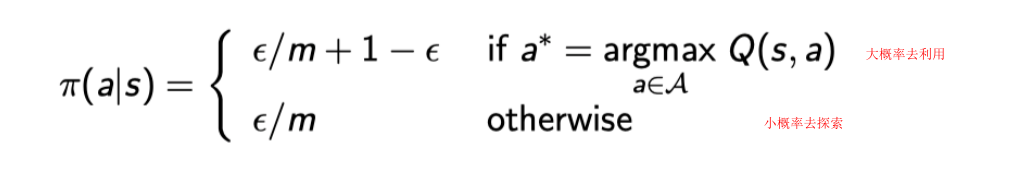
ε-greedy

综上，在轨MC控制即在每轮episode中，使用动作价值函数进行MC策略评估，使用ε-greedy进行策略优化

1.2 GLIE条件

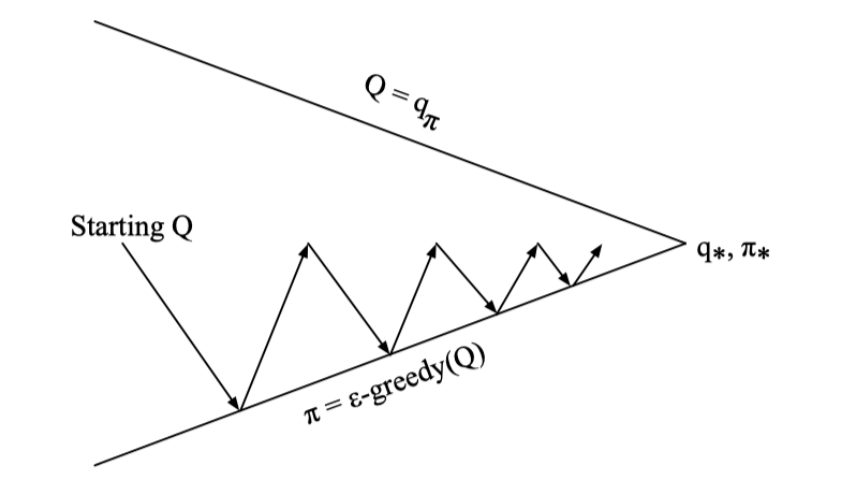
在机器学习中有这样一个说法，收敛到的值可能并不是全局最优而是局部最优，上述MC控制中就可能出现这样的情况，那么什么时候能够确定MC是收敛到最优值的呢？ – 满足GLIE条件

GLIE条件即在有限的时间内进行了无限可能的探索，这意味着所有的状态-动作都被探索了无数次

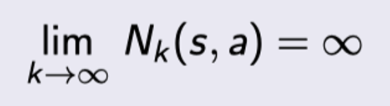
且最终收敛的策略趋于贪婪

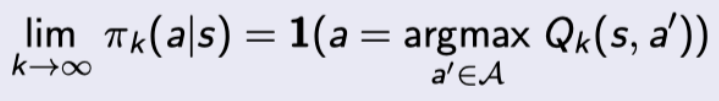
一个经典的满足GLIE条件的例子就是上述MC控制，但是其动作价值函数的优化策略ε-greedy中的ε=1/k

收敛到最优值的MC控制

2.在轨TD控制

因为MC只能用于完整的episode，所以需要介绍TD控制应用于在线学习中；

2.1 Sarsa算法

动作价值函数可以表示为如下形式

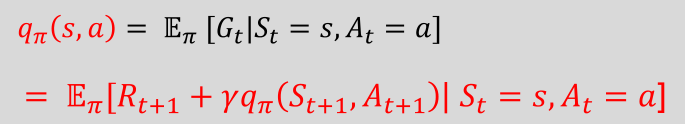
将TD的思想应用于Q(S,A)的第二种表达式中可以得到如下更新公式，这也是在轨策略评估计算动作价值函数的公式

Sarsa的策略优化仍然使用的是和在轨MC相同的ε-greedy策略；

Q：为什么要称为Sarsa算法？

A：将完整的episode拆分为每个时间步，也就是进行动作价值函数更新的最小单位，从上往下将字母拼接即为”Sarsa”

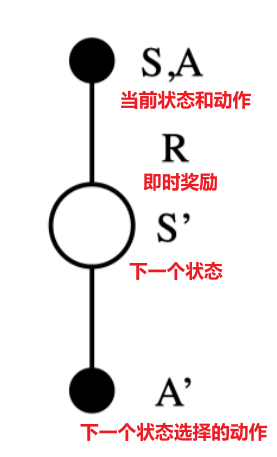
综上，Sarsa控制即在每个时间步中，使用Sarsa动作价值函数进行MC策略评估，使用ε-greedy进行策略优化

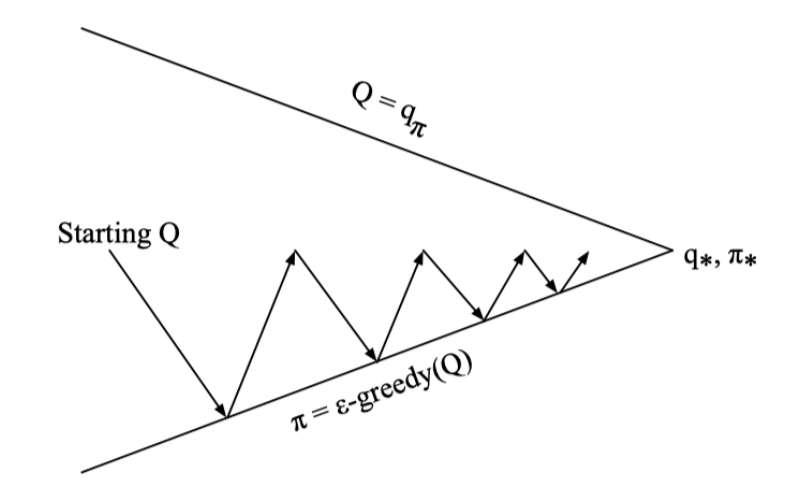
其综合算法如下

同在轨MC一样，Sarsa也不一定就是收敛到最优值的，Sarsa收敛于最优价值函数当且仅当满足：

  1. 任何时候的策略都满足GLIE特性
  2. 步长系数αt满足

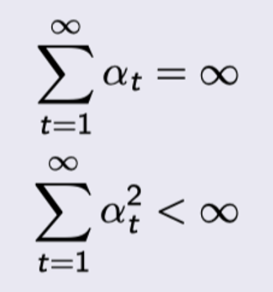
3.离轨TD控制

离轨学习主要有以下几个重要概念：

  • 目标策略：用来学习的策略，也就是观察者的策略
  • 行为策略：生成行动样本的策略，也就是游戏玩家的策略
  • 离轨学习中评估的目标都是目标策略（生成状态价值函数或动作价值函数），但是遵守的是行为策略 – 可以认为是游戏遵守的是游戏玩家的策略，而评估计算的是观察者的策略，因为观察者和游戏玩家会共享同一个Q函数（之后会介绍），所以观察者的策略会间接的影响游戏玩家的策略，但观察者无法直接影响游戏玩家的策略行为；
  • 观察者和游戏玩家不仅共享Q函数，实际上共享系统中所有的如St、Rt+1等因素，不同的只是两者在当前状态下选择的动作A

3.1 Q学习

Q学习考虑基于动作价值函数Q(s,a)的离轨学习，其用于自举的动作选择的是目标策略的后续状态对应的动作，而当前状态选择的动作是行为策略选择的当前状态对应的动作，因此Q学习的策略迭代表达式如下

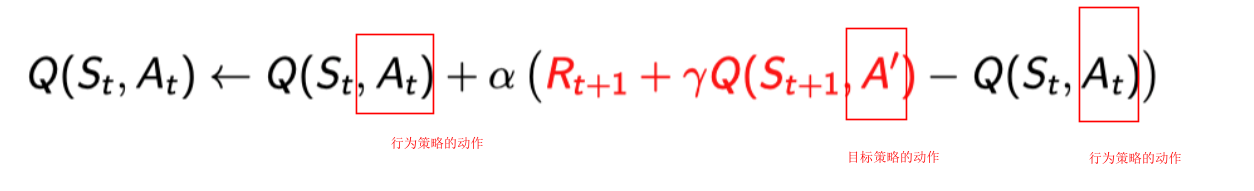
尽管观察者和游戏玩家共享Q函数，但它们对策略的优化是不同的，目标策略的优化使用的是最朴素的贪婪优化方式（无探索行为）

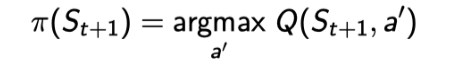
而行为策略的优化使用的是ε-greedy的方式（有探索行为，目标策略和行为策略不同的优化方式实现了Q学习在遵循探索性策略的同时学习最优策略）

将贪婪策略代入Q学习的策略迭代表达式，可以得到如下式子

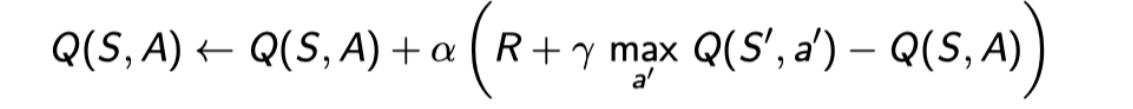
可以看到该表达式的形式非常类似[贝尔曼最优方程](#3.6 贝尔曼最优方程)；事实上，Sarsa中使用的是贝尔曼期望方程进行更新，而Q学习使用的是贝尔曼最优方程进行更新，因此Q学习收敛时一定会收敛到最优值；

Q学习的综合算法如下

4.Sarsa VS. Q-Learning

4.1 Q值更新

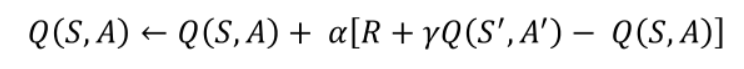
Sarsa更新公式

Sarsa的Q值更新公式中，R+γQ(S’,A’)可以视为目标Q值，Sarsa每次都是在下一次采取实际动作之后再更新Q值，A’表示下一次采取的实际action，Sarsa的每次更新都是在动作实际发生以后；

因为Sarsa是在实际动作发生后更新Q值，而采取ε-greedy策略会有一定概率进行探索，因此表现在悬崖问题中，Sarsa会选择离悬崖最远的路径（这样是最安全的）；

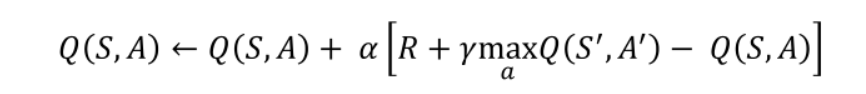
Q学习更新方式

Q学习的Q值更新公式表示，Q学习在更新Q值的时候下一步动作是不确定的，它会选择Q值最大的动作进行下一步的更新，表现在悬崖问题中，Q学习会选择离悬崖最近的路径，但是因为掉落次数较多所以分数低于Sarsa；

总的来说，Sarsa表现得更为胆小，因为它会记住每一次错误的探索，它会对错误较为敏感，而Q-learning只在乎Q值的最大化，因此Q-learning会十分贪婪，表现得十分大胆；

六、价值函数逼近

本章重点：DQN及其改进

现在希望用强化学习来解决状态空间很大的问题，如何将前面介绍过的强化学习方法应用到这类大型问题中实现预测和控制呢？

首先要明确，前面介绍的方法无论是针对状态价值函数V(s)还是动作价值函数Q(s,a)本质上都可以看作通过一个查找表来存储价值函数，比如对于动作价值函数来说存在一个Q表

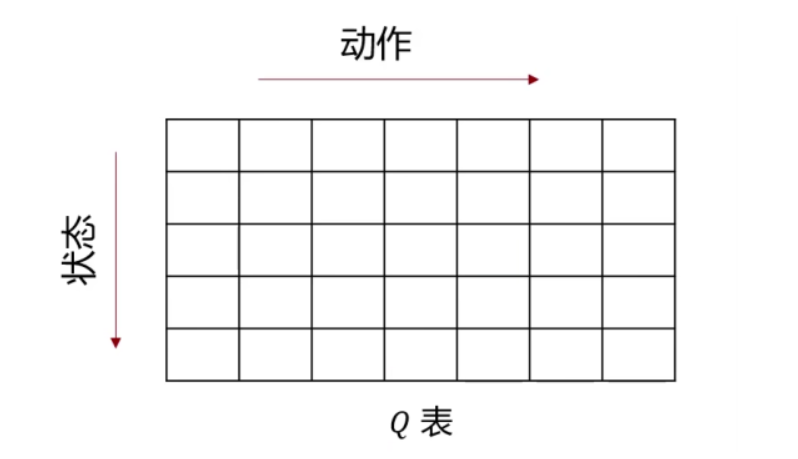
前面所介绍的方法都是解决将这张Q表的每一个格子都填满，但是对于大型MDPS问题来说，其状态和动作太多，无法全部存储在内存中，同时针对每一个状态和动作学习得到动作价值函数（填表过程）也是一个非常缓慢的过程，这导致无法直接将前面介绍的强化学习方法应用在大型MDPS任务；

考虑使用某个函数来拟合或逼近状态价值函数或动作价值函数，即

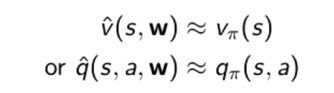
假设有一个函数q，权重参数为w，输入为s，a，输出为q，使用这个预测的q去逼近真实的Q表中的q值；使用这种函数逼近的方法可以用已知<状态，动作>学习得到的函数插值预测未出现过的<状态，动作>的动作价值函数；

价值函数的逼近类型主要有以下三种

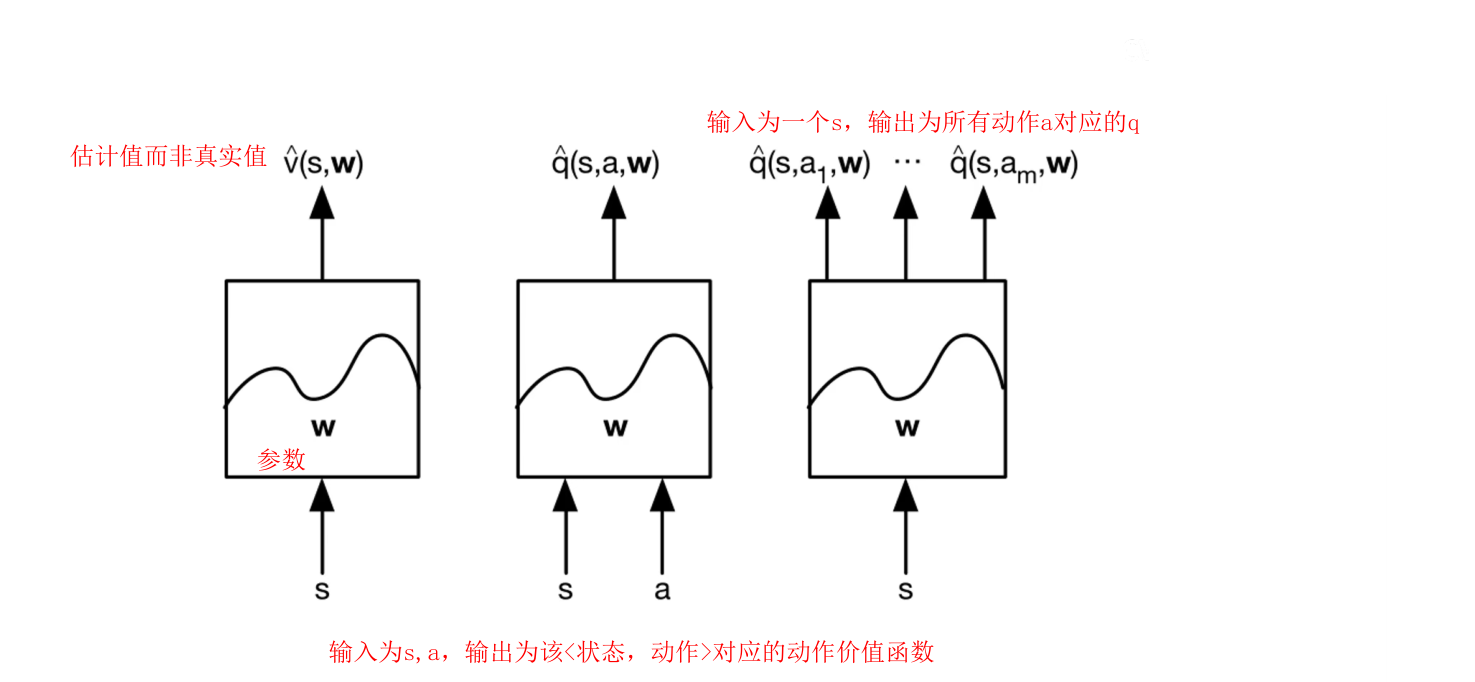
一般选择的逼近函数是可微分的函数，即特征的线性组合或神经网络（非线性），可微分意味着在之后的求导以及求最优值的阶段比较方便；

除了需要可微分的函数以外，还需要一种适用于非平稳，非独立同分布数据的训练方法（因为强化学习需要的样本是相关的，会导致模型出现过拟合；同时强化学习的过程不是平稳的，训练数据会实时更新）

1.前置知识

1.1 线性最小二乘拟合

线性表示使用的函数是线性函数，二乘表示损失函数是平方形式，最小表示拟合目标是需要对损失函数最小化

整个任务可以总结为用大量数据找出m和b即拟合直线，对于线性最小二乘拟合有两种解法，第一种是直接联立求解偏导为0的方程组

第二种是使用解析解的方式得到最终W矩阵的形式为

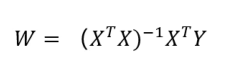
1.2 非线性最小二乘拟合

非线性最小二乘拟合与线性的区别在于使用的拟合函数是非线性的

1.3 梯度下降法

梯度下降法既可以用于线性最小二乘的求解，也可用于非线性最小二乘的求解

假设有如下非线性最小二乘任务

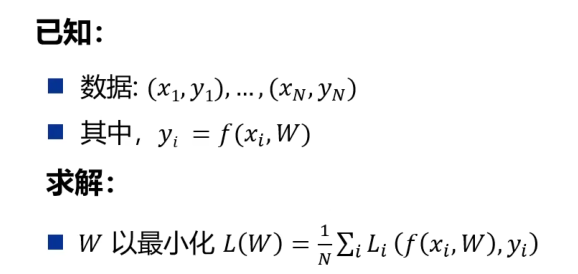
梯度下降法的思想很简单，就是不断计算梯度并更新权值接着再计算梯度重复更新权值直到收敛（即梯度为0）

针对上面的非线性最小二乘任务，使用梯度下降法的求解算法表达如下，其中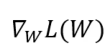表示对损失函数L(W)求偏导

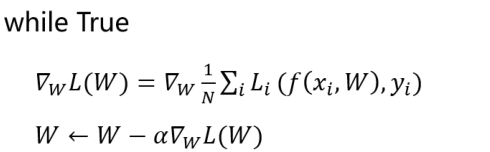
可以看到梯度下降算法的核心就是求解损失函数L(W)的梯度（偏导数变化最快的方向），因此常使用ΔW代替核心计算部分

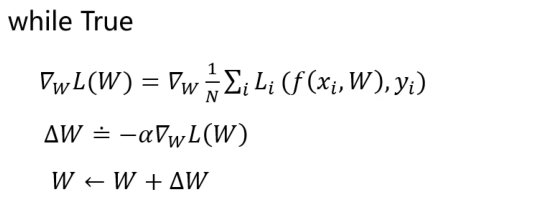
1.3.1 随机梯度下降

原始的梯度下降算法是利用所有样本计算损失并更新梯度，还是沿用上面的非线性最小二乘的例子，其梯度下降算法的中计算损失函数梯度的部分形式为

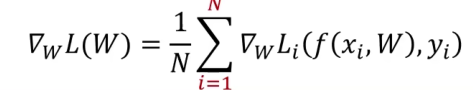
这样会导致一个问题就是如果样本量很大的时候更新一次W非常麻烦，可以使用随机梯度下降，即每次随机选择一个样本xi计算其损失函数的梯度

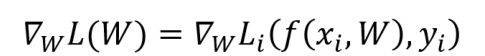
随机梯度下降的优势是每次迭代更新权重参数W的时间短，缺点是某些噪声点可能会导致梯度上升，不过整体的训练趋势仍然是下降

1.3.2 小批量梯度下降

将随机梯度下降和梯度下降算法进行折中得到小批量梯度下降，即每次随机选择所有样本中的m（超参数）个样本，计算损失并计算其梯度

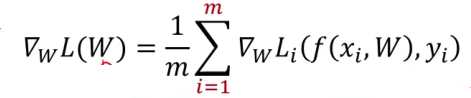
1.4 价值函数逼近

下面分别使用v’(S,w)函数和q’(S,A,w)函数来拟合真实的状态价值函数和动作价值函数

1.4.1 状态价值函数

假设我们使用v’(S,w)这个近似状态价值函数来逼近真实状态价值函数vΠ(s)，这里不考虑v’(S,w)是线性或非线性组合，均使用梯度下降进行求解

得到价值函数逼近任务的最小二乘损失函数J(w)定义（这个损失函数的定义是梯度下降的定义，随机梯度下降的损失函数定义去除前面的期望即可）

使用梯度下降算法对J(w)求梯度并使用Δw替代（期望更新等于全部梯度更新）

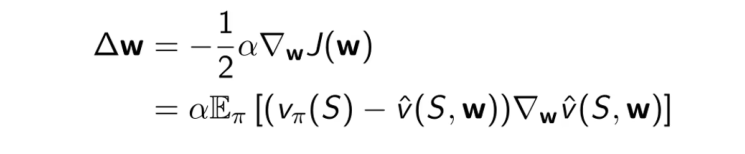
使用随机梯度下降算法对J(w)求梯度并使用Δw替代

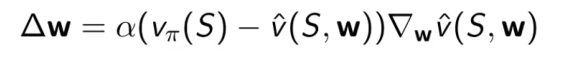
1.4.2 动作价值函数

动作价值函数的逼近如下（与状态价值函数类似故此处不赘述）

1.5 状态表示

在实际求解过程中需要使用特征向量或one-hot形式表示状态（原本的状态仅仅只是Q表中的序列）或者<状态，动作>（状态行为的特征向量与状态的特征向量表示类似，这里不多赘述）

1.5.1 特征向量

使用特征向量表示状态

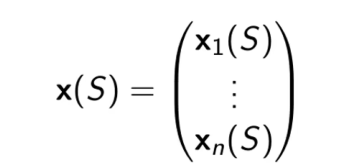
假如我们这里有一个任务，给出的近似状态价值函数是一个线性的组合

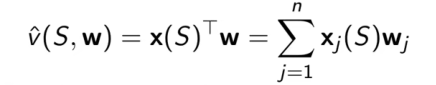
因为使用最小二乘法，所以定义的目标函数为

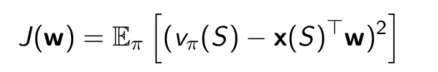
对于上述目标函数J(w)使用梯度下降算法收敛到全局最优，对J(w)计算梯度得到的Δw表达式如下（这个结论可以直接用于线性价值函数逼近的任务）

1.5.2 one-hot

使用one-hot方法简单来说就是将状态向量对应的位置的数值设置为1，主要记忆一个结论 – 使用one-hot编码状态的价值函数和权值一一对应

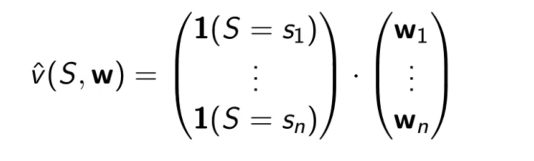
2.增量方法

增量方法实际上就是使用随机梯度下降对目标函数进行优化，预测任务就是求解价值函数，控制任务除了求解价值函数外还需要求解对应的最优策略；

2.1 增量式预测

2.1.1 状态价值函数

假如预先给定真实的状态价值函数vΠ(s)，则该问题可以建模为一个典型的有监督学习问题，但在强化学习中是无模型的，也就意味着不会有标签存在，因此实际计算过程中需要使用预测值target代替真实值vΠ(s)；

MC和TD对应的更新公式Δw分别如下

  • 蒙特卡洛评估收敛到局部最优（即使使用非线性值函数逼近）；
  • 线性TD（0）收敛（close）到全局最优；

2.2 增量式控制

2.2.1 动作价值函数

控制任务除了求解价值函数外还需要求解对应的最优策略，所以这里使用动作价值函数而不是状态价值函数，而动作价值函数和状态价值函数的近似函数、损失函数等都非常近似，因此不多赘述，参考[价值函数逼近](#1.4 价值函数逼近)

有了动作价值函数的表示方法之后就可以使用它进行更新，与预测方法类似，这里使用target替代真实的动作价值函数qΠ(S,A)，MC和TD对应的更新公式Δw分别如下

3.批量方法

前面介绍的增量方法基于随机梯度学习，但是对于随机梯度学习来说样本的使用效率不高，这里采用小批量梯度下降的方法，因为RL的训练数据有一定相关性，所以需要随机采样尽量使得小批量的样本没有相关性；

这里假设存在一个状态价值函数的近似v’(s,w)，以及一段时间内的训练数据，批量方法同样是使得最小二乘算法找到参数w，使得目标值和近似值之间的平方和误差最小，与增量方法的区别就在于其损失函数的表示方法是一个批量中的数据差异求和而非单个样本的差异

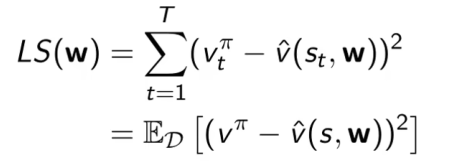
优化LS(w)的方法并不唯一，除了使用半梯度下降的方式，还可以对这个batch中的每一个样本应用随机梯度下降，收敛至这个batch的最小平方差的参数，这个参数w就是针对这个batch最优的权值参数，我们称这样的优化方法为带经验回放的随机梯度下降；

Google对经验回放的描述为，是一种用于增强学习的技术，其主要思想是将智能体（agent）在环境中的经验存储在一个经验回放池（Experience Replay Buffer）中，然后在训练期间，从中随机取出一些经验进行训练；

经验回放的主要优点是：

  1. 减少了数据的相关性：由于训练数据是随机抽样的，因此可以减少数据之间的相关性，从而提高训练的稳定性。
  2. 提高了样本效率：由于数据可以被重复利用，因此可以在更少的样本数量下实现更好的训练效果。
  3. 支持离线学习：由于数据被存储在经验回放池中，智能体不必等待新的经验就可以进行训练，从而支持离线学习。

3.1 DQN

DQN是非线性逼近的代表（因为其使用的逼近函数是神经网络），DQN就是在传统Q learning的基础上做了三个改进，使得其效果上升显著；

DQN主要对Q learning做了如下创新：

  1. DQN利用深度卷积神经网络来逼近值函数，跟之前讲的线性逼近不同，这里是用神经网络来进行的非线性逼近，而且用的是强大的深度卷积神经网络，也就是CNN。
  2. DQN利用了经验回放对强化学习的学习过程进行训练， DQN 有一个记忆库用于学习之前的经历. 所以每次 DQN 更新的时候, 都可以随机抽取一些之前的经历进行学习. 随机抽取这种做法打乱了经历之间的相关性, 也使得神经网络更新更有效率。
  3. DQN独立设置了目标网络来单独处理时间差分算法中的TD偏差。目标网络也是一种打乱相关性的机理。DQN 中使用到两个结构相同但参数不同的神经网络,其中需要评估 的Q 神经网络具备最新的参数, 而目标 Q 神经网络使用的参数则是很久以前的。这样的方式也能让训练变得更加有效，更具有鲁棒性

DQN的基本算法代码如下

七、策略梯度方法

本章重点：REINFORCE

到目前为止，学习了关于有模型MDP（在实际中不常见），无模型MDP的的解决。对于有模型，用动态规划法，对于无模型，用采样的算法（TD，MC等）来策略估计，然后再进行策略提升（贪婪，Ɛ-贪婪）。接着学习了在无模型策略估计中用函数逼近思想代替传统用表方法，来适应更多大规模的实际问题。以上所有总结起来都是以值函数为中心来解决MDP的，也就是策略估计+策略提升的过程，这一节以策略为中心解决MDP问题；

2023/5/29 21:22 这学期时间太紧张了，这后面的部分感兴趣可以看视频自学，后面应该就不会再更新强化学习知识点相关的内容了。接下来就介绍一些课程内的作业以及对应的解决方法。

八、Gymnasium库

有关Gymnasium库的详细介绍都在其官方文档上Gymnasium Documentation (farama.org)；

Gymnasium是OpenAI Gym库的一个维护分支，Gym库是一个用于开发和比较强化学习算法的工具包。Gymnasium以原始Gym库的功能为基础，并为工具包添加了额外的环境。与Gym一样，Gymnasium用于开发、测试和比较强化学习算法（Gymnasium对旧的Gym环境兼容）；Gymnasium包括各种各样的环境，包括经典的控制任务、雅达利游戏、机器人模拟等等，这些环境提供了一种测试和比较强化学习算法的标准化方法，使研究人员和开发人员更容易构建和评估他们的模型；

Q：Gym库和Gymnasium库的关系和区别是什么？

A：Gymnasium库是为了解决原始Gym库中的问题和限制创建的，Gymnasium库并不是OpenAI Gym库的官方组成部分，其开发和维护主要由开源社区驱动；

Gymnasium库与OpenAI Gym库保持API兼容性，因此使用Gym编写的代码通常也适用于Gymnasim，然而，由于Gymnasium包含了额外的功能和改进，可能会发现在与某些环境交互或注册自定义环境的方式上存在一些差异；

总的来说熟悉Gym库的使用，则对于Gymnasium库的上手不会有任何问题，主要区别就在于Gymnasium包含了一些额外的功能和改进，可以使其更容易地在某些类型的环境中工作；

1.Gym简介

（因为网上有关Gymnasium库的介绍非常少，所以可以直接找Gym库的教程看，几乎是差不多的）

OpenAl Gym 是一款用于研发和比较强化学习算法的工具包，它支持训练智能体（agent）做任何事–从行走到玩Pong 或围棋之类的游戏都在范围中。
OpenAl Gym是一个用于开发和比较RL算法的工具包，与其他的数值计算库兼容，如tensorfiow或者theano库。现在主要支持的是python语言，以后将支持其他语言。
OpenAI Gym包含两部分：

  1. gym 开源包含一个测试问题集，每个问题成为环境（environment），可以用于自己的强化学习算法开发，这些环境有共享的接口，允许用户设计通用的算法，例如：Atari、CartPole 等。
  2. OpenAl Gym 服务提供一个站点和 api，允许用户对自己训练的算法进行性能比较。

强化学习是机器学习的一个分支，目的是开发出智能体（Agent）做出决策和控制，但是，RL面临以下挑战：

  1. 更好的benchmarks：在监督学习中有ImageNet，而强化学习只有庞大的环境集合。但是目前这些环境还是缺少多样性。
  2. 缺少标准化的环境：环境中很小的差异将大大改变问题的难度，因此发表过的研究工作无法重现和比较。

Gym库的出现解决了RL面临的问题。

2.Gymnasium入门

Gymnasium的API有四个主要的函数：make、reset、step和render；

Gymnasium的核心在于Env，这是一个高级python类，代表强化学习理论中的马尔可夫决策过程（官网介绍说这不是一个完整的reconstruction，缺少了MDPS的一些组成部分），在gyumnasium中，MDPS环境作为Env和Wrappers实现，可以更改传递给用户的结果；

通过如下命令在conda虚拟环境中安装Gymnasium库

1
pip install Gymnasium -U

但仅仅使用上面命令安装的库会缺少一些依赖，比如

因此推荐使用下面的命令安装所有依赖

1
pip install "Gymnasium[all]"

安装报错（更推荐安装gym）：

Q：在安装BOX2D的时候会报错“Microsoft Visual C++ 14.0 or greater is required”；

A：出现上述报错是因为pip所安装的包需要使用C++编译后才能够正常安装，但是当前安装环境中缺少完整的C++编译环境，因此安装失败，所以使用conda命令就不会出现这种问题；

Q：明明conda成功安装了BOX2D为什么还是说没有这个module？

A：BOX2D真正的问题不在于是否使用conda命令安装，而是必须要借助swig安装whl版本的BOX2D，解决参考

解决这个报错花费了我大量时间，简单记录一下心得：下次解决报错的时候，多看看文章，不要一来就无脑跟着某个文章磕，先大概知道报错的原因再解决；

2.1 初始化环境

通过make()初始化环境，该函数包括许多用于添加Wrappers、为环境指定关键字等附加参数

1
2
import gymnasium as gym # 注意大小写，一定不要写成Gymnasium
env = gym.make('CartPole-v1')

这将返回一个可以与用户交互的Env，使用如下命令查看所有可以创建的环境（包括许多用于添加Wrappers、为环境指定关键字等的附加参数）

1
gymnasium.envs.registry.keys()

2.2 环境交互

下图是一个经典的“agent-env loop”，也是Gymnasium实现RL的简化表示

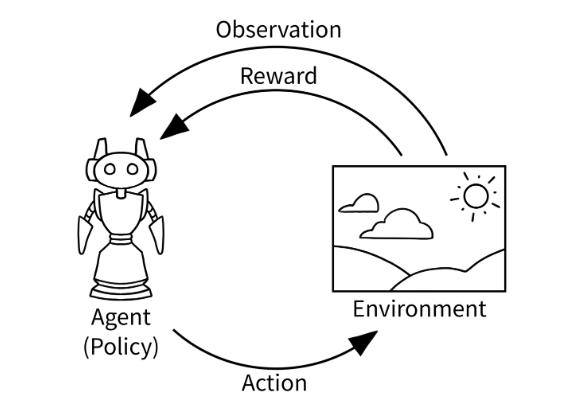
上述循环可以使用下面的代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import gymnasium as gym
# 首先使用make创建一个环境（此处使用“LunarLander”环境，即agent控制着一艘需要安全着陆的宇宙飞船），关键字render_mode指定了环境应该如何可视化
env = gym.make("LunarLander-v2", render_mode="human")
# 初始化环境后，reset环境以获得对环境的第一次观测，reset可以使用seed或options参数指定特定的随机种子或选项
observation, info = env.reset()
# agent在环境中执行动作step，从而导致环境发生变化，接着agent从更新后的环境中接收到新的观察结果以及奖励，一个这样的action-observation交换称为一个timestep
for _ in range(1000):
    action = env.action_space.sample()  # agent policy that uses the observation and info
    observation, reward, terminated, truncated, info = env.step(action)
# 经过一段时间后，环境可能会结束，这被称为终端状态，Gymnasium中环境终止则returned by step，当然也可以手动设置在固定的timesteps后环境结束，此时环境发出truncated信号，无论哪种情况，都需要调用reset来重新启动环境
    if terminated or truncated:
        observation, info = env.reset()

env.close()

代码运行后将呈现如下效果图

每个环境都使用env.action_space和env.observation_space属性指定有效操作和观测的格式。这有助于了解环境的预期输入和输出，因为所有有效的行动和观察都应包含在相应的空间中（即action spaces和observation spaces）；每个环境都应该具有action_space和observation_space属性，这两个属性都应该是从space继承的类的实例，Gymnasium支持用户可能需要的大多数可能的空间：

  • Box:描述了一个n维连续空间。这是一个有界空间，在这里我们可以定义上限和下限，这些上限和下限描述了我们的观测可以取的有效值；
  • Discrete:描述了一个离散空间，其中{0，1，…，n-1}是我们的观察或行动可以采取的可能值。可以使用可选参数将值移位到｛a，a+1，…，a+n-1｝；
  • Dict:表示简单空间的字典；
  • Tuple:表示简单空间的元组；
  • MultiBinary:创建一个n形二进制空间，参数n可以是一个数字或数字列表；
  • MultiDiscrete:由一系列Discrete动作空间组成，每个元素中有不同数量的动作；

Wrappers是一种修改现有环境的快捷方法而无需更改底层代码，使用wrappers可以避免大量样板代码并使得环境更加模块化，wrappers也可以被链接以组合它们的效果；

大多数通过Gymnasium.make生成的环境默认情况下已经使用TimeLimit、OrderEnforceing和PassiveEnvChecker进行了包装；

Gymnasium提供许多常用的wrappers：

  • TimeLimit:如果超过了最大时间步数（或基本环境已发出截断信号），则发出截断信号；

  • ClipAction:剪裁动作，使其位于动作空间中（类型为Box）；

  • RescaleAction:将操作重新缩放到指定的间隔内；

  • TimeAwareObservation:将有关时间步长索引的信息添加到观测中。在某些情况下，有助于确保转换是马尔可夫的；

如果已经有一个wrapped的环境，并且你想在所有包装层下面获得unwrapped的环境（这样就可以手动调用一个函数或更改环境的一些底层方面），可以使用.unpacked属性。如果环境已经是一个基本环境，那么.unpacked属性只会返回自身；

3.Frozen Lake环境

3.1 环境简介

FrozenLake 是典型的具有离散状态空间的 Gym 环境，agent的任务是学会从起点走到目的地并不能掉进hole。

Frozen Lake游戏中，一块冰面上有四种state：

  • S: initial stat 起点
  • F: frozen lake 冰湖
  • H: hole 窟窿，可用于结束一个回合
  • G: the goal 目的地，可用于结束一个回合

利用matplotlib可以查看冰冻湖的原始图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import gymnasium as gym
import matplotlib.pyplot as plt

env = gym.make('FrozenLake-v1', desc=["SFFF", "FHFH", "FFFH", "HFFG"], map_name="4x4", is_slippery=True,render_mode='rgb_array')

# Reset the environment to a random initial state
obs = env.reset()

# Render the environment as an RGB array
img = env.render()

# Plot the RGB image using matplotlib
plt.imshow(img)
plt.show()

绘制的图像如下

可将上述冰冻湖转换为如下图例

冰冻湖的状态个数为16(0-15)，行为个数为4(LEFT=0；DOWN=1；RIGHT=2；UP=3)，需要注意的是，在 FrozenLake 环境中，由于冰面很滑，因此智能体不会始终按照指定的方向移动。例如，当执行向下移动的动作时，智能体也可能向左或向右移动（当然可以在后续将is_slipper关闭，则动作的随机性消失）。

如果满足以下两个条件之一，则回合将终止：

  • 智能体移动到 H 格子(状态 5、7、11 或 12)：产生的总奖励为 0
  • 智能体移动到 G 格子(状态 15)：产生的总奖励为 +1

Frozen Lake的源码中的step部分如下（这是Gym中的step，Gymnasium中的step中间的done被拆分为terminated和truncated返回）

1
2
3
4
5
6
7
def step(self, a):
	transitions = self.P[self.s][a]
	i = categorical_sample([t[0] for t in transitions], self.np_random)
	p, s, r, d = transitions[i]
	self.s = s
	self.lastaction = a
	return (int(s), r, d, {"prob": p})

即step部分接受动作a并返回状态s，奖励r，是否接收d以及转移概率p，其中转移概率的通俗解释为“在当前的状态，如果动作向左，就会有向着除了反方向之外的格子1/3的概率”

1
2
3
4
For example, if action is left and is_slippery is True, then:
         - P(move left)=1/3
         - P(move up)=1/3
         - P(move down)=1/3

实验的目标是设计算法使agent能够学习得到最好的策略，即在每个状态选择最优的动作，最终能够到达终点。

在开始之前我们不妨让agent选择随机策略，即在每个状态随机从(0,3)之间随机选取一个数字作为action_index执行动作，看看效果怎么样（返回的矩阵表示agent在冰冻湖的位置，返回的元组第一个参数表示next_state，第二个参数表示rewards，这个参数只有在达到终点的时候才是1，第三个参数表示事件是否结束）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
count = 0
while True:
    count = count+1
    action=random.randint(0,3)
    env.print_current_state()
#     time.sleep(1)
    new_observation=env.step(action) #这里的接收的new_observation元组分别是当前状态、奖励以及指示事件是否结束
    print(new_observation)
    print('\n')
    if new_observation[2]: #如果事件结束则reset状态（不管奖励是否>1，先判定事件是否结束）
        env.reset()
    if new_observation[1]>0: #如果奖励>0 ,也就是到达目的地，则退出循环
        print('Reach goals,try '+str(count)+'times')
        break

随即策略因为是agent随机选择的策略，所以就算我们的action是确定的，但是agent仍然需要执行很多次的尝试

可以看到使用随即策略需要不断尝试1306次才能使得agent从起点走到终点，下面的图是agent的最后一次尝试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
X F F F
F H F H
F F F H
H F F G
(0, 0, False)


X F F F
F H F H
F F F H
H F F G
(4, 0, False)


S F F F
X H F H
F F F H
H F F G
(8, 0, False)


S F F F
F H F H
X F F H
H F F G
(9, 0, False)


S F F F
F H F H
F X F H
H F F G
(10, 0, False)


S F F F
F H F H
F F X H
H F F G
(14, 0, False)


S F F F
F H F H
F F F H
H F X G
(14, 0, False)


S F F F
F H F H
F F F H
H F X G
(15, 1, True)

可见使用随机策略不是一个可行的方式，下面将分别使用动态规划的方法和无模型控制的方法为agent寻找最优策略。

3.2 问题解决

3.2.1 策略迭代算法

参考链接：《Hands-on RL》动态规划算法_天池notebook-阿里云天池 (aliyun.com)；

策略迭代算法对当前的策略进性策略评估，得到其状态价值函数，然后用该状态价值函数根据策略提升来得到一个更好的新策略，然后再继续评估新策略再提升策略，以此往复，直至最后收敛到最优策略。

策略评估的伪代码如下

策略提升的伪代码如下

(1)算法设计

如伪代码所示，策略迭代算法主要分为三个部分：策略评估、策略提升以及策略迭代，我们分别介绍。

首先是策略评估，主要思想是计算当前策略pi的状态价值函数v，并通过迭代所有状态，计算每个状态-操作对的期望值来评估当前策略。

  • 策略评估算法首先将所有状态的值函数v初始化为零；

  • 在环境中的所有状态上迭代，对于每个状态，在所有操作上迭代，以计算每个操作的预期回报qsa；预期回报是通过将所有可能的下一个状态的奖励和discounted的未来收益求和，并按其概率加权来计算；

  • 循环持续直到所有状态的新的和旧的值函数之间的最大差值小于给定的阈值θ；

  • 最后使用更新后的值函数来评估策略；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def policy_evaluation(self):
        while 1:
            delta = 0 # 每次迭代开始时初始化为0，以跟踪值函数的最大变化
            new_v = [0] * self.env.ncol * self.env.nrow # 将状态值函数v初始化为零
            for s in range(self.env.ncol * self.env.nrow): # 在环境中所有状态上循环，实现在状态空间列表上迭代
                exp_list = []
                for a in range(4): # 对于每个状态s，迭代所有动作来计算每个状态的状态值函数
                    exp = 0 # 用于跟踪状态s中每个动作a的预期回报
                    for res in self.env.P[s][a]: # 预期回报是通过在状态s中对采取行动a的所有可能结果进行循环
                        # 预期回报=下一状态next_state的奖励和discounted value之和
                        exp += res[0] * (res[2] + self.gamma * self.V[res[1]]*(1-res[3]))
                    # 将所有操作的加权预期回报相加来计算状态s的新值
                    exp_list.append(self.policy[s][a] * exp)
                new_v[s] = sum(exp_list)
                # 计算新的和旧的状态值函数之间的最大差值
                delta = max(delta, abs(new_v[s] - self.V[s]))
            # self.v变量被更新为新的值函数new_v
            self.V = copy.deepcopy(new_v)
            if delta < self.theta:
                break
        print('Policy Evaluation Done!')

接着是策略提升，策略提升函数的输入为当前状态值函数self.v，更新策略self.pi，简单来说策略提升的目标是更新agent的策略以选择每个状态的期望积累奖励最大化的操作。

  • 策略提升对环境中所有可能的状态进行迭代，对每个状态使用贝尔曼方程计算每个可能action的期望回报，每个action的期望返回存储在该状态对应的q值列表中；
  • 选择具有最高q值的action，同时将选择这些action中的每一个的概率设置为1除以具有最高q值的动作的数量，其他action概率设置为0；
  • 函数返回更新后的policy，用于之后的策略评估和策略提升；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def policy_improvement(self):# 策略提升，agent通过选择使每个状态的预期discounted累积奖励最大化的操作来更新其策略
        for s in range(self.env.ncol * self.env.nrow):# 在环境中所有可能的状态s上循环
            exp_list = []
            for a in range(4):
                exp = 0# 对于每个状态s，agent计算每个可能动作的预期siacounted积累奖励
                for res in self.env.P[s][a]:
                    # 贝尔曼方程 qsa = sum(p * (r + gamma * v(next_state)) for p, next_state, r, done in P[s][a])
                    # P[s][a]是一组可能的下一个状态、奖励和转换到下一个状态的概率
                    exp += res[0] * (res[2] + self.gamma * self.V[res[1]]*(1-res[3]))
                exp_list.append(exp)
            max_exp = max(exp_list)# 选择最大值maxq并计算具有该最大值的动作数量cntq
            cnt_max = exp_list.count(max_exp)
            # 所有具有最大动作值的动作被选中的概率相等，而所有其他动作的概率为0
            self.policy[s] = [1 / cnt_max if q == max_exp else 0 for q in exp_list]
        print('Policy Improvement Done!')
        return self.policy

最后是策略迭代部分，策略迭代指的是agent与env交互学习得到policy，使得期望的积累回报最大化；

  • 策略迭代函数通过交替调用策略评估和策略提升算法，直至策略收敛，收敛指的是当策略在两个连续的迭代之间不再改变即old_policy=new_policy；
1
2
3
4
5
6
7
8
def policy_iteration(self):
        while 1:
            self.policy_evaluation() # 调用policy_evaluation函数，通过计算当前策略的状态值函数v来评估该策略
            old_policy = copy.deepcopy(self.policy)# 将列表进行深拷贝，方便接下来进行比较
            new_policy = self.policy_improvement()# 调用policy_improvement函数，通过选择最大化预期长期回报的行动（即行动值函数q）来改进当前策略
            if old_policy == new_policy:
                break
        print('Policy Iteration Done!')
(2)策略实践

首先执行train函数，进入训练阶段，也就是不断进行策略迭代

1
2
3
4
# 策略迭代
print('PolicyIteration Beginning...')
agent = PolicyIterationAgent(env, theta, gamma)
agent.policy_iteration()

训练完成得到如下输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
PolicyIteration Beginning...
Policy Evaluation Done!
Policy Improvement Done!
Policy Evaluation Done!
Policy Improvement Done!
Policy Evaluation Done!
Policy Improvement Done!
Policy Iteration Done!
------------------OptimalValue------------------
 0.590  0.656  0.729  0.656 
 0.656  0.000  0.810  0.000 
 0.729  0.810  0.900  0.000 
 0.000  0.900  1.000  0.000 
------------------OptimalPolicy------------------
State 0 -> Optimal Action:↓
State 0 -> Optimal Action:→
State 1 -> Optimal Action:→
State 2 -> Optimal Action:↓
State 3 -> Optimal Action:←
State 4 -> Optimal Action:↓
State 5 -> Optimal Action: Hole
State 6 -> Optimal Action:↓
State 7 -> Optimal Action: Hole
State 8 -> Optimal Action:→
State 9 -> Optimal Action:↓
State 9 -> Optimal Action:→
State 10 -> Optimal Action:↓
State 11 -> Optimal Action: Hole
State 12 -> Optimal Action: Hole
State 13 -> Optimal Action:→
State 14 -> Optimal Action:→
State 15 -> Optimal Action: End

可以看到在动作无随机性的情况下策略迭代进行了三轮，即交替执行三次策略评估和策略提升，最终得到每个状态对应的最优价值。

最优策略显示了在某个状态时可以选择执行的action，推导的原则为若邻居状态的价值大于当前状态的价值函数则向邻居状态移动，因此也可以看到有些状态如0既可以向下移动也可以向右移动，因为这两个方向的价值函数均大于0状态本身的价值函数。

拥有了最优策略我们就可以将该策略给agent，指导agent成功的从起点移动到终点，下面执行test函数（test函数的原理非常简单，就是根据agent的policy在每个状态选择action并输出可视化结果）对得到的最优策略进行检验，得到如下输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
------------------Game Beginning...------------------
X F F F
F H F H
F F F H
H F F G
Current selection action:
↓

S F F F
X H F H
F F F H
H F F G
Current selection action:
↓

S F F F
F H F H
X F F H
H F F G
Current selection action:
→

S F F F
F H F H
F X F H
H F F G
Current selection action:
↓

S F F F
F H F H
F F F H
H X F G
Current selection action:
→

S F F F
F H F H
F F F H
H F X G
Current selection action:
→

Reach the goal!
------------------Game Ending...------------------

X表示agent当前所在位置，Current selection action表示agent在当前状态选择的action，依据是前面得到的最优策略（如果某个状态对应两个动作则随机从中选取一个动作）。

可以很直观的从图中看到，agent成功的从起点到达终点，并且成功的避免了掉进冰窟中或移动到grid外面。

3.2.2 价值迭代算法

(1)算法设计

价值迭代本质上是策略迭代的策略评估只进行一次退化得到，经过与贪婪算法的整合之后就得到了贝尔曼最优方程，因此价值迭代的本质就是通过使用Bellman方程重复计算每个状态的期望值并找到所有可能动作的最大期望值来更新v列表，直到新旧值函数之间的差值小于theta阈值，收敛后得到的策略就是最优策略。

下面的价值迭代通过迭代计算值函数和最优策略求解最优策略

  • 将所有状态对应的价值函数和阈值theta初始化为0，while循环退出的条件是值函数的最大差值小于阈值theta；
  • new_v列表将存储迭代过程中的更新的值函数；
  • 对于每个状态s，算法使用当前值函数来计算每个动作a的期望值Q，这通过迭代在状态s中采取action的所有可能结果完成，采取的action由状态转移矩阵确定；
  • 一旦已经为状态s中的所有动作计算了Q值，该算法就将状态s的值设置为所有动作的最大Q值，这对应于贝尔曼最优方程；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
while 1:
            delta = 0
            new_v = [0] * self.env.ncol * self.env.nrow
            # 对于每个状态s，函数计算每个动作a的期望值，并选择使该值最大化的动作
            for s in range(self.env.ncol * self.env.nrow):
                exp_list = []# 用于存储每个状态-动作对的Q值，Q值是通过在特定状态s中采取特定动作a而获得的未来奖励的预期总和
                for a in range(4):# 对于每个动作a
                    exp = 0
                    for res in self.env.P[s][a]:# 使用当前值函数计算采取该操作的预期值
                        exp += res[0] * (res[2] + self.gamma * self.V[res[1]]*(1-res[3]))
                    exp_list.append(exp)# 将此值添加到列表qsa_list中
                    # 一旦已经为状态s中的所有动作计算了Q值，该算法就将状态s的值设置为所有动作的最大Q值，这对应于贝尔曼最优方程
                new_v[s] = max(exp_list)
                # 将new_v中的状态值设置为qsa_list中的最大值 ，该方程指出，一个状态的最优值等于所有可能行动的未来回报的最大预期总和
                delta = max(delta, abs(new_v[s] - self.V[s]))
            self.V = copy.deepcopy(new_v)
            if delta < self.theta:
                break
        print('Value Iteration Done!')
  • 计算出值函数之后，算法通过选择每个状态s下使得期望最大对应的action导出策略policy，如果有多个动作具有相同的期望值，则算法为策略中的这些动作分配相等的概率；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
for s in range(self.env.ncol * self.env.nrow):
            exp_list = []
            for a in range(4):
                exp = 0
                for res in self.env.P[s][a]:
                    # 使用最优值函数self.v计算每个状态-动作对的Q值
                    exp += res[0] * (res[2] + self.gamma * self.V[res[1]]*(1-res[3]))
                exp_list.append(exp)
            max_exp = max(exp_list)
            cnt_max = exp_list.count(max_exp)
            # 将具有最大Q值的动作的概率设置为1，并将所有其他动作的概率设为0来提取每个状态的最优策略
            # 让相同的动作价值均分概率
            self.policy[s] = [1 / cnt_max if q == max_exp else 0 for q in exp_list]
        print('Policy Improvement Done!')
(2)策略实践

此处的train和test方法与前面策略迭代相同，只需要将train的参数从PolicyIteration修改为ValueIteration，train的结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
ValueIteration Beginning...
Value Iteration Done!
Policy Improvement Done!
------------------OptimalValue------------------
 0.590  0.656  0.729  0.656 
 0.656  0.000  0.810  0.000 
 0.729  0.810  0.900  0.000 
 0.000  0.900  1.000  0.000 
------------------OptimalPolicy------------------
State 0 -> Optimal Action:↓
State 0 -> Optimal Action:→
State 1 -> Optimal Action:→
State 2 -> Optimal Action:↓
State 3 -> Optimal Action:←
State 4 -> Optimal Action:↓
State 5 -> Optimal Action: Hole
State 6 -> Optimal Action:↓
State 7 -> Optimal Action: Hole
State 8 -> Optimal Action:→
State 9 -> Optimal Action:↓
State 9 -> Optimal Action:→
State 10 -> Optimal Action:↓
State 11 -> Optimal Action: Hole
State 12 -> Optimal Action: Hole
State 13 -> Optimal Action:→
State 14 -> Optimal Action:→
State 15 -> Optimal Action: End

可以看到价值迭代的结果和策略迭代的结果完全一致，从理论上来说也应当是一致的，因此验证了算法的正确性，根据train得到的策略进行test的结果如下，这与策略迭代的移动轨迹也是相同的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
------------------Game Beginning...------------------
X F F F
F H F H
F F F H
H F F G
Current selection action:
↓

S F F F
X H F H
F F F H
H F F G
Current selection action:
↓

S F F F
F H F H
X F F H
H F F G
Current selection action:
→

S F F F
F H F H
F X F H
H F F G
Current selection action:
↓

S F F F
F H F H
F F F H
H X F G
Current selection action:
→

S F F F
F H F H
F F F H
H F X G
Current selection action:
→

Reach the goal!
------------------Game Ending...------------------

3.2.3 Q-learning算法

参考链接：Q-learning：thanusiv/Frozen-Lake-With-Q-Learning: Implemented Frozen Lake game with Q-Learning from scratch (github.com)；

Q学习算法的伪代码如下

(1)算法设计

Q-learning算法的核心在于在每个episode上迭代并根据当前state和Q表选择action，同时根据收到的rewards和下一状态的最大Q值更新Q表，最终理论上会得到一张对应最优策略的Q表。

  • 初始化Q表（存储每个<状态，动作>对的Q值）并在指定数量的episodes上迭代，每个episode都是agent和env之间的完整交互；
  • 在每个episode中agent使用ε贪婪探索策略基于Q表中的Q值来选择动作，ε值随着时间的推移衰减；
  • Q值使用贝尔曼方程更新，基于获得的rewards和下一个状态的最大Q值来更新；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def Q_Learning(self):
        for episode in range(self.episodes):
            total_reward = 0# 初始化当前episode的reward为0
            state = self.env.reset()# 重置当前状态为起始状态
            for step in range(self.max_steps):# 在max_steps_per_set范围内的每个步骤上循环
                rand = random.uniform(0,1)
                # 如果随机生成的数字小于探索率，则使用环境的get_random_action（）方法选择一个随机操作
                if rand < self.epsilon:
                    action = self.env.get_random_action().value
                # 否则使用numpy的argmax（）方法为当前状态选择Q值最高的动作，以检索Q值最高动作的索引
                else:
                    action = np.argmax(self.Q[state,:])
                # 使用环境的step方法将所选action作用在环境上，step返回下一个状态、采取动作的奖励以及指示事件是否完成的布尔值
                new_state,reward,done = self.env.step(action)
                # 更新当前<状态，动作>对的Q值
                self.Q[state][action] = self.Q[state][action] * (1 - self.learning_rate) + \
                                                    self.learning_rate * (
                                                            reward + self.discount_rate * np.max(
                                                        self.Q[new_state, :]))
                # 更新当前状态
                state = new_state
                # 用从action中获得rewards更新当前episode的总奖励
                total_reward += reward
                if done:# 假如该episode已完成，则循环中断
                    break
            # 每次episode结束后，通过使用指数衰减函数将探索率从最大值逐渐降低到最小值来更新探索率
            self.epsilon = self.epsilon_min + (self.epsilon_max - self.epsilon_min) * np.exp(-self.epsilon_decay * episode)
            # 将当前eposide获得的总奖励存储在一个名为total_reward的列表中
            self.rewards.append(total_reward)
(2)策略实践

该部分同样分为两部分，train部分初始化环境后，传入env以实例化一个QlearningAgent类对象，将其命名为agent也就是小机器人，调用小机器人的Q_Learning方法即可开始执行Q-Learning算法得到最优策略，通过agent的print_result方法可视化训练结果。

1
2
3
4
5
6
7
8
9
10
def train():
    env = FrozenLake()
    agent = QlearningAgent(env)
    agent.Q_Learning()
    agent.print_results(['←', '↓', '→', '↑'],[5, 7, 11, 12], [15])
    return agent
def test(agent):
    print('------------------Game Beginning...------------------')
    agent.latest_iteration()
    print('------------------Game Ending...------------------')

test部分调用agent的latest_iteration方法对训练得到的最优策略（实际上是基于最后一次迭代得到的Q表，但当时已经收敛因此可以看作是最优策略）进行测试，latest_iteration部分的基本思想就是agent从起点开始根据训练得到的Q表，根据当前状态选择action中概率最大的action执行，以此类推，最终到达终点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def latest_iteration(self):
     state= self.env.reset()
     for step in range(self.max_steps):
        self.env.print_current_state()
        time.sleep(1)
        action = np.argmax(self.Q[state,:])
        print('当前选择动作：')
        self.print_action(action)
        print('\n')
        new_state,reward,done = self.env.step(action)
        state = new_state
        if done:
            print('Reached the goal')
            break

先看train得到的结果，分别对Q表、最优策略以及平均奖励做了可视化。

其中最优策略就是选择Q表中的每个状态的action列表中概率最大的action_index对应的action，通过平均奖励也可以看出在训练了8000个episodes之后agent就已经确定了最终的最优策略，故奖励不再增大，代表整个算法收敛。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
------------------Q-Table------------------
[[9.41480149e-01 9.50990050e-01 9.32065348e-01 9.41480149e-01]
 [9.41480149e-01 0.00000000e+00 7.29121367e-01 9.13888936e-01]
 [8.76578874e-01 2.08886992e-01 1.28175264e-02 8.17249166e-02]
 [1.60521527e-01 0.00000000e+00 6.43730402e-07 6.43730402e-07]
 [9.50990050e-01 9.60596010e-01 0.00000000e+00 9.41480149e-01]
 [0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 8.83844680e-01 0.00000000e+00 9.06726299e-02]
 [0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
 [9.60596009e-01 0.00000000e+00 9.70299000e-01 9.50990049e-01]
 [9.60596009e-01 9.80100000e-01 9.80099987e-01 0.00000000e+00]
 [9.28975931e-01 9.90000000e-01 0.00000000e+00 6.85405926e-01]
 [0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 9.80099955e-01 9.90000000e-01 9.70298900e-01]
 [9.80099980e-01 9.89999995e-01 1.00000000e+00 9.80099955e-01]
 [0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]]
------------------OptimalPolicy------------------
State 0 -> Optimal Action:↓
State 1 -> Optimal Action:←
State 2 -> Optimal Action:←
State 3 -> Optimal Action:←
State 4 -> Optimal Action:↓
State 5 -> Optimal Action: Hole
State 6 -> Optimal Action:↓
State 7 -> Optimal Action: Hole
State 8 -> Optimal Action:→
State 9 -> Optimal Action:↓
State 10 -> Optimal Action:↓
State 11 -> Optimal Action: Hole
State 12 -> Optimal Action: Hole
State 13 -> Optimal Action:→
State 14 -> Optimal Action:→
State 15 -> Optimal Action: End
------------------AverageRewards------------------
1000 :  0.265
2000 :  0.741
3000 :  0.9
4000 :  0.96
5000 :  0.973
6000 :  0.988
7000 :  0.988
8000 :  0.991
9000 :  0.991
10000 :  0.991

使用收敛之后得到的Q表对agent的行为进行指导，我们得到在test上的行进路线（这个路线和策略迭代、价值迭代是相同的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
------------------Game Beginning...------------------
X F F F
F H F H
F F F H
H F F G
当前选择动作：
↓

S F F F
X H F H
F F F H
H F F G
当前选择动作：
↓

S F F F
F H F H
X F F H
H F F G
当前选择动作：
→

S F F F
F H F H
F X F H
H F F G
当前选择动作：
↓

S F F F
F H F H
F F F H
H X F G
当前选择动作：
→

S F F F
F H F H
F F F H
H F X G
当前选择动作：
→

Reached the goal
------------------Game Ending...------------------

3.3 随机动作

Frozen Lake游戏有一个很有意思的地方，在于可以将冰面的属性设置为slippered，这意味着agent选择执行的动作并不一定会执行，而有可能以等概率的形式执行除了选择方向反方向的三个方向之一，可以通过下面的代码验证

1
2
3
4
5
6
7
8
import gymnasium as gym
import copy
import numpy as np
from copy import deepcopy

env = gym.make("FrozenLake-v1",is_slippery=False)  # 创建环境
for a in env.P[14]:  # 查看终点左边一格的状态转移信息 -- 每个动作都会等概率滑行到3种可能结果（一行对应一个动作的3种可能）
    print(env.P[14][a])

输出结果如下

1
2
3
4
[(0.3333333333333333, 10, 0.0, False), (0.3333333333333333, 13, 0.0, False), (0.3333333333333333, 14, 0.0, False)]
[(0.3333333333333333, 13, 0.0, False), (0.3333333333333333, 14, 0.0, False), (0.3333333333333333, 15, 1.0, True)]
[(0.3333333333333333, 14, 0.0, False), (0.3333333333333333, 15, 1.0, True), (0.3333333333333333, 10, 0.0, False)]
[(0.3333333333333333, 15, 1.0, True), (0.3333333333333333, 10, 0.0, False), (0.3333333333333333, 13, 0.0, False)]

上面代码的意思是指查看14状态的状态转移信息，这意味着每个动作都会等概率({‘prob’: 0.3333333333333333}))滑行到3种可能结果（一行对应一个动作的3种可能）。

那么当冰面变得光滑的时候动态规划算法或Q-learning算法是否还起作用呢？我们选择策略迭代算法进行检验，只需要将env的初始化中is_slippered修改为True即可。

执行完策略迭代的train算法后得到如下结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
------------------状态价值------------------
 0.069  0.061  0.074  0.056 
 0.092  0.000  0.112  0.000 
 0.145  0.247  0.300  0.000 
 0.000  0.380  0.639  0.000 
------------------最优策略------------------
State 0 -> Optimal Action:←
State 1 -> Optimal Action:↑
State 2 -> Optimal Action:←
State 3 -> Optimal Action:↑
State 4 -> Optimal Action:←
State 5 -> Optimal Action: Hole
State 6 -> Optimal Action:←
State 6 -> Optimal Action:→
State 7 -> Optimal Action: Hole
State 8 -> Optimal Action:↑
State 9 -> Optimal Action:↓
State 10 -> Optimal Action:←
State 11 -> Optimal Action: Hole
State 12 -> Optimal Action: Hole
State 13 -> Optimal Action:→
State 14 -> Optimal Action:↓
State 15 -> Optimal Action: End

这个结果比较令人惊讶，如处于状态0的时候选择的是向左移动，直观感受是agent会移动出grid，但是因为冰面光滑的原因，导致agent要么向左要么向上要么向下，因为向左和向上都会出grid，但是向下会得到更高的价值。根据冰面滑行的原则，是可以理解的为什么不选择直观方向的。

在冰面光滑的条件下agent的移动就不是action唯一指定了，可以看下面的test，因为动作具有随机性所以agent可能移出grid、掉进冰窟，这就导致agent需要重新从起点开始，因此agent明显尝试的次数相较于确定性动作多得多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
X F F F
F H F H
F F F H
H F F G
当前选择动作：
←

S F F F
X H F H
F F F H
H F F G
当前选择动作：
←

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
F H F H
F X F H
H F F G
当前选择动作：
↓

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
X H F H
F F F H
H F F G
当前选择动作：
←

X F F F
F H F H
F F F H
H F F G
当前选择动作：
←

S F F F
X H F H
F F F H
H F F G
当前选择动作：
←

X F F F
F H F H
F F F H
H F F G
当前选择动作：
←

S F F F
X H F H
F F F H
H F F G
当前选择动作：
←

X F F F
F H F H
F F F H
H F F G
当前选择动作：
←

X F F F
F H F H
F F F H
H F F G
当前选择动作：
←

S F F F
X H F H
F F F H
H F F G
当前选择动作：
←

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
X H F H
F F F H
H F F G
当前选择动作：
←

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
F H F H
F X F H
H F F G
当前选择动作：
↓

S F F F
F H F H
F F F H
H X F G
当前选择动作：
→

S F F F
F H F H
F X F H
H F F G
当前选择动作：
↓

S F F F
F H F H
X F F H
H F F G
当前选择动作：
↑

S F F F
F H F H
F X F H
H F F G
当前选择动作：
↓

S F F F
F H F H
F F F H
H X F G
当前选择动作：
→

S F F F
F H F H
F F F H
H X F G
当前选择动作：
→

S F F F
F H F H
F F F H
H F X G
当前选择动作：
↓

S F F F
F H F H
F F F H
H F X G
当前选择动作：
↓

Reach the goal!
专业课
#机器学习
强化学习
https://gintoki-jpg.github.io/2023/02/27/专业_强化学习/
作者
杨再俨
发布于
2023年2月27日
许可协议