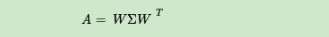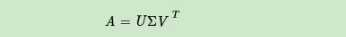任务:分别基于SVD分解以及基于SGNS两种方法构建汉语子词向量并进行评测。
参考链接:
2023/5/6 16:50 现在一整个都是懵的状态,因为根本就不知道要做什么,这个实验的目的是什么,是否有什么前置知识点(SVD奇异值分解)。因此现在的首要任务是先知道我们这个实验要做什么,然后再细看文档。
2023/5/6 20:14 现在理解了基本原理,也知道要做什么了,然后也找到了参考代码,推荐先用便于理解的notebook代码,行不通再看另一个;
2023/5/6 22:48 第一份代码写的很好,但是因为没有相关的训练文件所以实际上我跑了一遍根本不知道在干什么(理解原理不动手实操没什么用…),现在尝试第二份代码,理解透彻后对第一份代码进行理解或直接使用第二份代码(因为第二份代码的语料什么的都已经准备好了,所以就算不使用第二份的代码仍然可以使用其语料);
2023/5/7 10:41 现在已经把代码、语料文件等统统完成,接下来只需要等待训练完成,了解实验原理、按照任务要求书写实验报告即可;
一、背景介绍 1.SVD原理 SVD代表奇异值分解。它是一种矩阵分解技术,将一个矩阵分解为三个矩阵,有助于降低原始矩阵的维数并提取重要特征。
在SVD中,矩阵a被分解为三个矩阵:U、∑和V^T^,其中U和V^T^是正交矩阵,∑是对角线上具有奇异值a的对角矩阵。奇异值是A^T^A或AA^T^的特征值的平方根。
1.1 特征值分解 若下面等式成立
其中A是一个n*n的方阵,x是一个n维向量,则称λ是矩阵A的一个特征值,而x是矩阵A的特征值λ对应的特征向量。
特征值和特征向量的意义在于矩阵A的信息可以由其特征值和特征向量表示。
假如已知矩阵A的n个特征值
其中W是由n个特征向量组成的n*n的方阵,Σ为以这n个特征值为主对角线的n*n方阵。
一般情况下,我们会将这n个特征向量进行标准化(具体方式这里不介绍)即满足
总结:矩阵的特征值表示的是该矩阵的重要程度,特征向量表示对应的特征值是什么
1.2 SVD分解 1.2.1 概述 特征值分解是一个提取矩阵特征很不错的方法,但是特征值分解的变换矩阵必须是方阵,而实际问题中的大部分矩阵并不是方阵,这就引出使用奇异值分解来描述普通矩阵的重要特征。
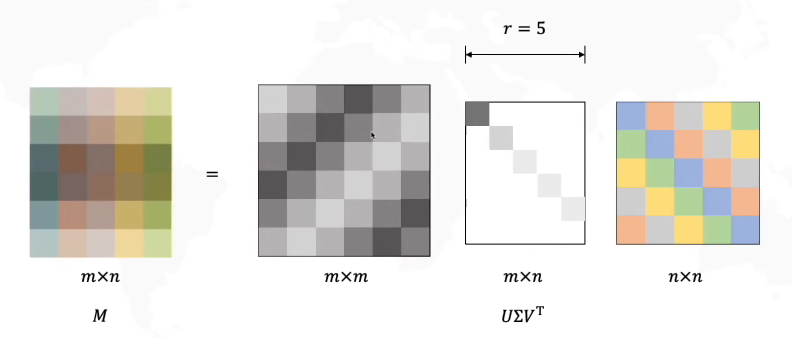
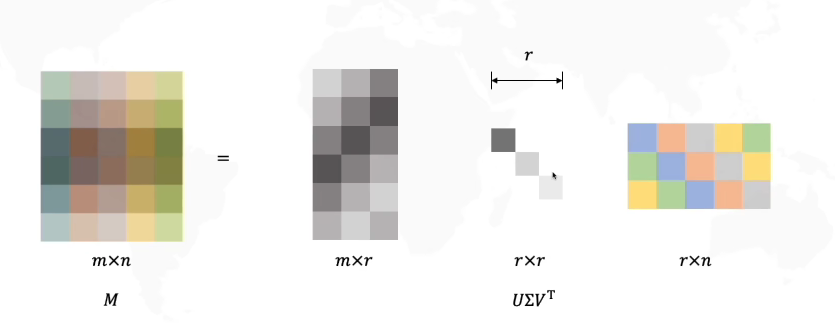
奇异值分解是指将任意m*n矩阵A表示为如下形式
U是一个m*m的正交矩阵;
Σ是一个m*n的矩阵,该矩阵除了主对角线上的元素外其余元素均为0,而主对角线上的每个元素都被称为奇异值;
V是一个n*n的正交矩阵;
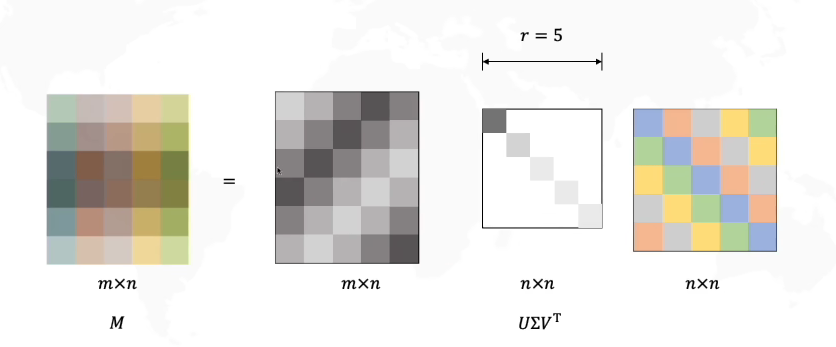
因为Σ矩阵的后面几行可能是全部为0的(至少图中是这样),因此可以对上述形式进行缩减
进一步的,对于Σ矩阵中的奇异值,因为它按照从大到小的顺序排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。这意味着可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵,这就实现了在保留最多信息的同时进行数据的压缩。
1.2.2 求解 奇异值分解的难点在于,求解分解后的U、Σ和V这三个矩阵,这里直接给出求解方法
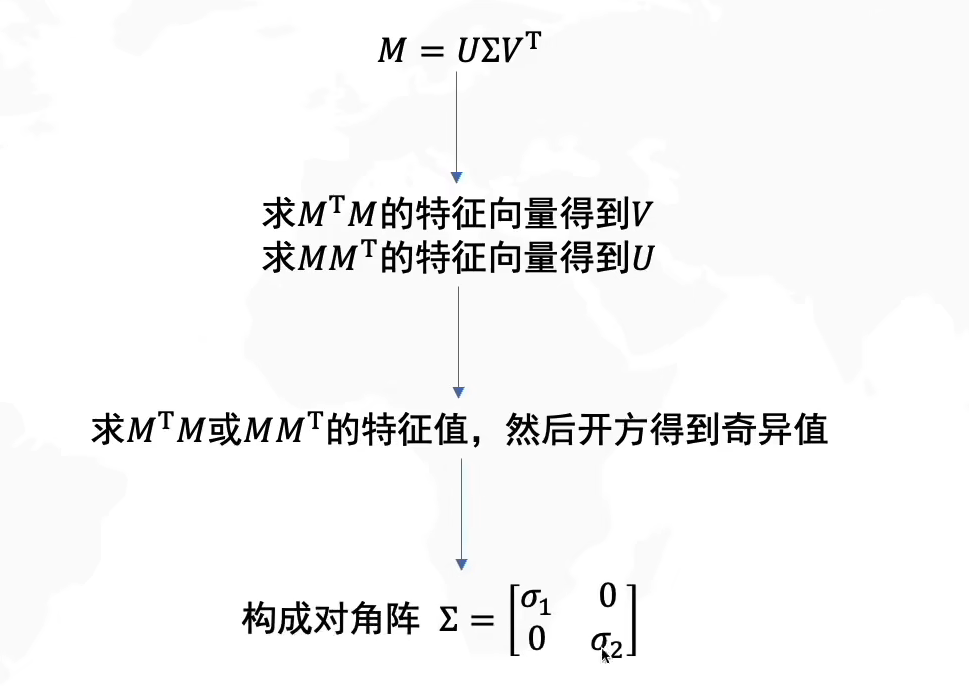
综上,求解一个原始矩阵M的SVD分解矩阵的步骤如下
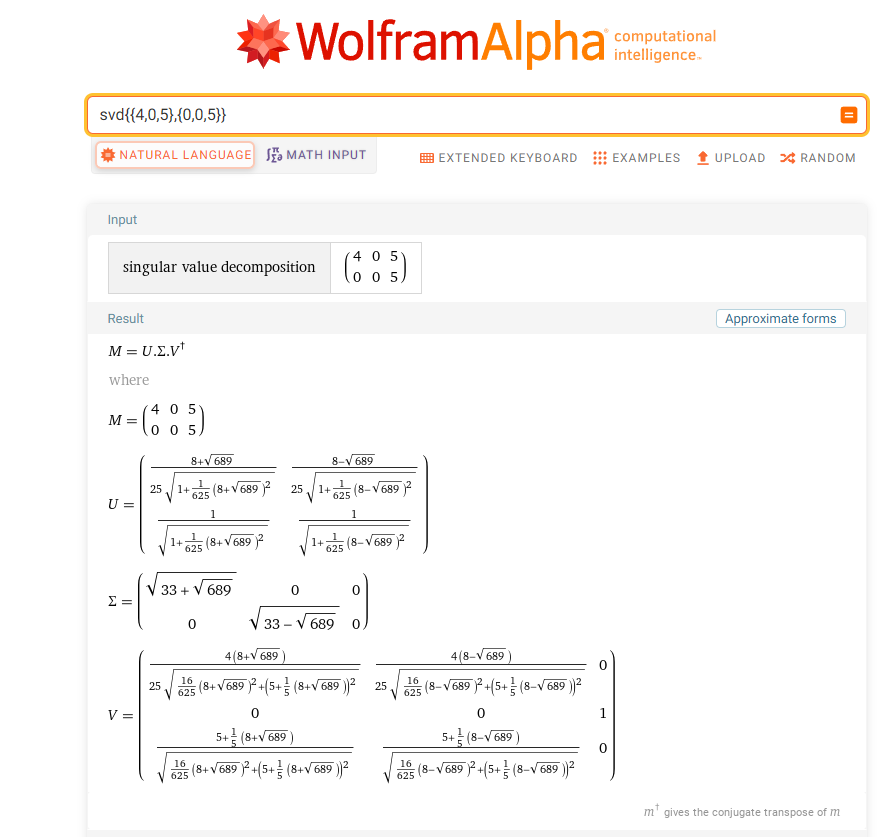
可以借助工具WolframAlpha 计算矩阵M的奇异值以及分解矩阵
2.SGNS算法 带负采样的Skip-gram(SGNS)是一种流行的机器学习算法,用于生成单词嵌入,是原始的Skip-gram算法的变体。
在SGNS中,该算法试图通过从词汇表中抽取反例来预测给定目标词周围的上下文单词。负样本是指没有出现在目标单词的上下文中的单词。该算法调整单词的数字表示(即嵌入),以最大化正确预测上下文单词的概率,并最小化预测负样本的概率。
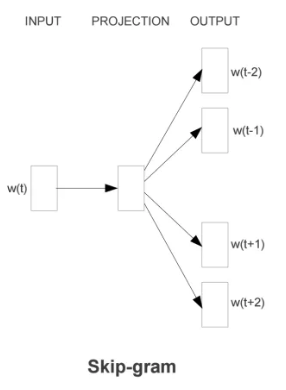
2.1 Skip-gram模型
Skip-Gram模型的基础形式非常简单,模型实际上分为两部分,第一部分为建立模型,第二部分是通过模型获取嵌入词向量。
Skip-Gram的整个建模过程实际上与自编码器(auto-encoder)的思想很相似,即先基于训练数据构建一个神经网络,当这个模型训练好以后,我们并不会用这个训练好的模型处理新的任务,我们真正需要的是这个模型通过训练数据所学得的参数,例如隐层的权重矩阵 – 这些权重在Word2Vec中实际就是“word vectors”。基于训练数据建模的过程被称为“Fake Task”,意味着建模并不是最终的目的。
当构建好一个完整的神经网络后,就需要对其进行训练,下面是训练步骤(假设训练语料为“The dog barked at the mailman”):
选择句中任一单词作为input word;
定义The dog barked at the mailman参数,该参数表示基于input word为中心的窗口范围内的所有单词都将被选取,假如该参数为2则获取的词为[‘The’, ‘dog’,’barked’, ‘at’];
定义num_skips参数,表示从整个窗口中选取多少个不同的词作为训练样本,假如该参数为2时,将会得到两组 (input word, output word) 形式的训练数据,即 (‘dog’, ‘barked’),(‘dog’, ‘the’);
神经网络基于这些训练数据将会输出一个概率分布,这个概率代表着我们的词典中的每个词是output word的可能性;
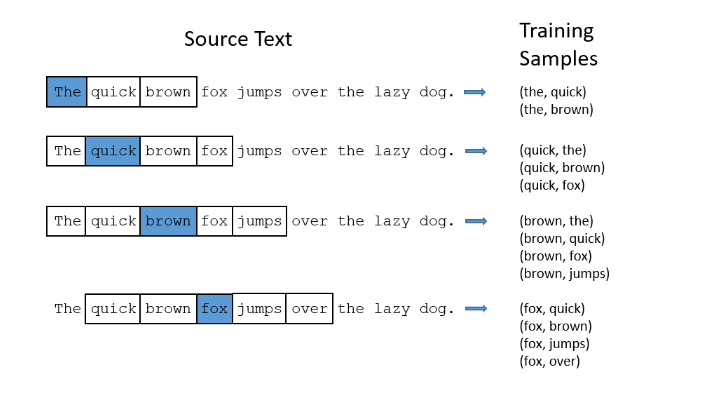
假如有“The quick brown fox jumps over lazy dog”,且设置窗口大小为2,则可以获取到如下训练样本
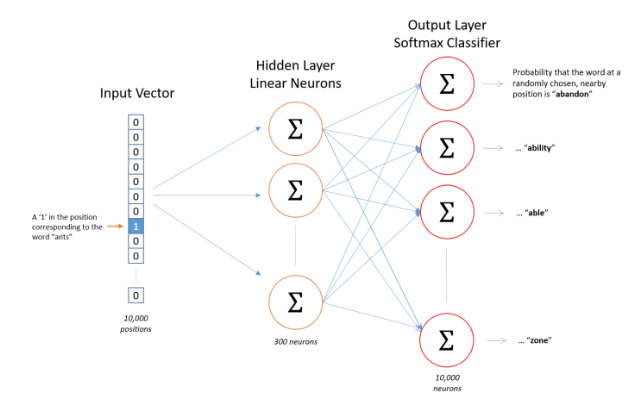
模型的输入如果为一个10000维的向量,那么输出也是一个10000维度(词汇表的大小)的向量,它包含了10000个概率,每一个概率代表着当前词是输入样本中output word的概率大小
模型的输出概率表示词典中每个词有多大可能性与input word同时出现(如果向神经网络模型中输入一个单词“Soviet“,那么最终模型的输出概率中,像“Union”,“Russia”这种相关词的概率将远高于像“watermelon”,“kangaroo”非相关词的概率。因为“Union”,“Russia”在文本中拥有更大的可能在“Soviet”的窗口中出现)
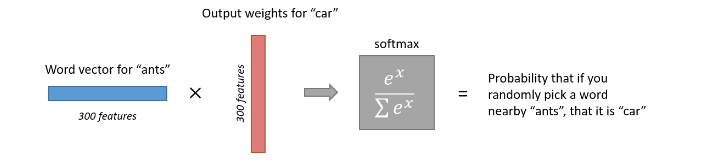
下面是一个例子,训练样本为 (input word: “ants”, output word: “car”) 的计算示意图
经过神经网络隐层的计算,ants这个词会从一个1 x 10000的向量变成1 x 300的向量,再被输入到输出层。输出层是一个softmax回归分类器,它的每个结点将会输出一个0-1之间的值(概率),这些所有输出层神经元结点的概率之和为1。
2.2 负采样 训练一个神经网络意味着要输入训练样本并且不断调整神经元的权重,从而不断提高对目标的准确预测。每当神经网络经过一个训练样本的训练,它的权重就会进行一次调整。
vocabulary的大小决定了Skip-Gram神经网络将会拥有大规模的权重矩阵,所有的这些权重需要通过数以亿计的训练样本来进行调整,这是非常消耗计算资源的,并且实际中训练起来会非常慢。
负采样(negative sampling)解决了这个问题,它是用来提高训练速度并且改善所得到词向量的质量的一种方法。不同于原本每个训练样本更新所有的权重,负采样每次让一个训练样本仅仅更新一小部分的权重,这样就会降低梯度下降过程中的计算量。
当用训练样本 ( input word: “fox”,output word: “quick”) 来训练神经网络时,“ fox”和“quick”都是经过one-hot编码的。如果vocabulary大小为10000时,在输出层期望对应“quick”单词的那个神经元结点输出1,其余9999个都应该输出0。在这里,这9999个期望输出为0的神经元结点所对应的单词称为 negative word 。当使用负采样时,将随机选择一小部分的 negative words (比如选5个 negative words )来更新对应的权重,同时也会对 positive word 进行权重更新(在上面的例子中,这个单词指的是”quick“)。
对于小规模数据集,选择5-20个negative words会比较好,对于大规模数据集可以仅选择2-5个negative words
一个单词被选作negative sample的概率跟它出现的频次有关,出现频次越高的单词越容易被选作negative words。
3.词向量构建 词向量的重要性在其他文章中已经声明过很多次,一般来说构建词向量主要有两种方式 – 基于计数和基于迭代(因为本部分知识点较重要所以有必要复习一遍)
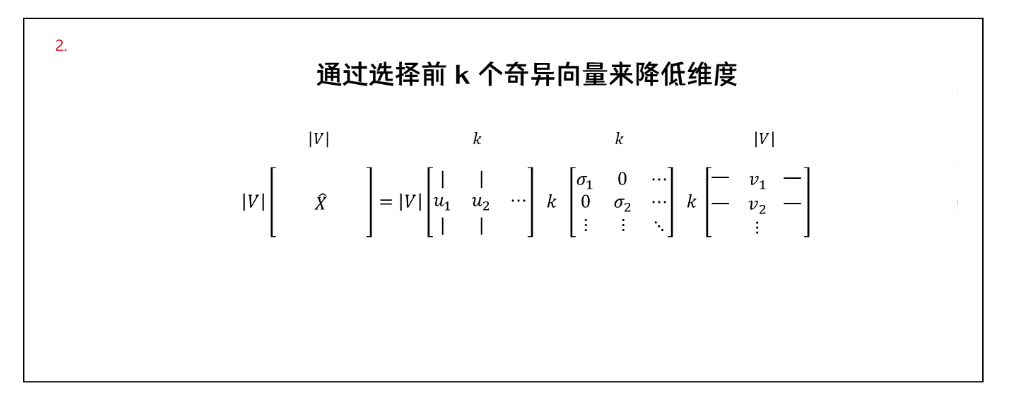
3.1 基于SVD降维的词向量 基于词共现矩阵X与SVD分解是构建词嵌入(即词向量)的一种方法:
首先遍历一个很大的数据集,统计词的共现计数矩阵X
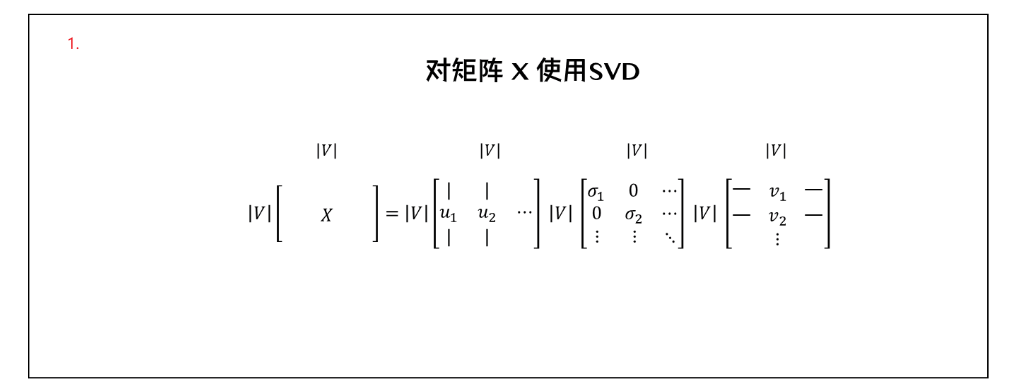
然后对矩阵X进行SVD分解得到USV^T^
使用U的行作为词典中所有词的词向量
共现矩阵主要有以下几种:
词-文档矩阵:依据是相关连的单词在同一个文档中会经常出现,因此遍历文档,当词i出现在文档j中,对Xij加1操作,得到的矩阵X规模与文档数量M成正比,即矩阵规模一般较大;
基于滑窗:上面那种方法除了矩阵规模较大外,执行全文档的统计也很耗时,可以调整为对一个窗口内的文本进行统计,即计算每个单词在特定大小的窗口中出现的次数,得到共现矩阵X。下面这个示例的滑动窗口大小为2对文本进行共现矩阵的构建
在得到了共现矩阵X后,对其执行SVD可以得到X=USV^T^,此时需要观察奇异值(即矩阵S的对角线元素),根据方差百分比留下前k个元素,取子矩阵U1:|V|,1:k作为词嵌入矩阵(简单来说就是将巨⼤的共现矩阵进⾏ SVD 分解后,选取最重要的⼏个特征值,得到每个词的低维表示)
基于SVD降维的词向量存在如下问题:
矩阵的维度会经常发生改变(经常增加新的单词和语料库的大小会改变);
矩阵会非常的稀疏,因为很多词不会共现;
矩阵维度一般会非常高;
需要在共现矩阵X上加入一些技巧处理来解决词频的极剧的不平衡;
并且基于SVD的计算复杂度很高,同时很难合并新单词或文档,当然用以下方法也可以在一定程度上解决上述问题:
忽略功能词,例如“the”,“he”,“has”等等
使用ramp window,即根据文档中单词之间的距离对共现计数进行加权
使用皮尔逊相关系数并将负计数设置为0,而不是只使用原始计数
我们所熟知的Word2Vec算法也是一种词向量的构建方法,与基于计数的共现矩阵不同,基于迭代的方式可以在控制复杂度的情况下有效地在大语料库上构建词向量
3.2 Word2Vec迭代算法
Word2Vec依赖于语言学中一个非常重要的假设「分布相似性」,即相似的词有相似的上下文
Word2Vec是一个迭代模型,该模型能够根据文本进行迭代学习,并最终能够对给定上下文的单词的概率对词向量进行编码呈现。
Word2Vec的基本思想是初始化一个模型,该模型的参数就是词向量,模型训练的任务是在每次模型的迭代过程中计算误差并基于优化算法调整模型参数(词向量)以减小损失函数,从而最终学习到词向量。
这种基于迭代的方法一次只会捕获一个单词的共现情况,与共现矩阵捕获所有共现计数区别
Word2Vec主要包含两个模型:
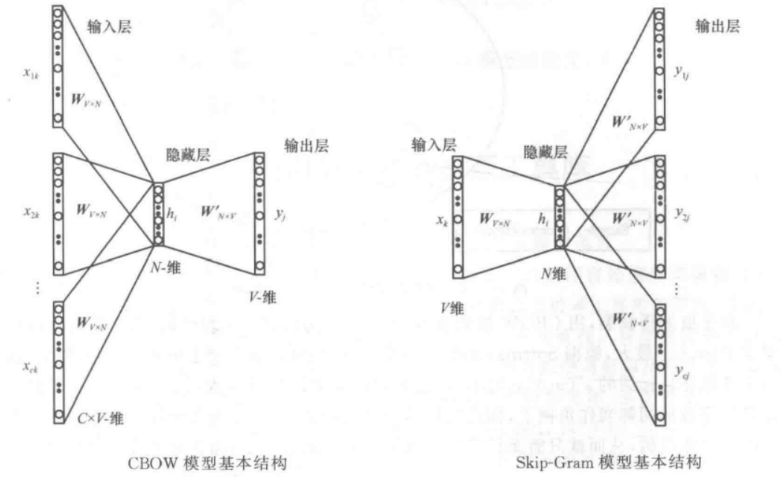
continuous bag-of-words(CBOW):CBOW方法是用周围词预测中心词,从而利用中心词的预测结果不断地调整周围词的向量。训练完成后,每个词都会作为中心词,对周围词的词向量进行调整,从而获得整个文本里所有词的词向量。CBOW对周围词的调整是统一的:求出的梯度的值会同样地作用到每个周围词的词向量当中去。所以CBOW预测行为的次数跟整个文本的词数几乎是相等的(每次预测行为才会进行一次反向传播,这也是最耗时的部分),复杂度是O(V);
skip-gram:Skip-Gram 是用中心词来预测周围的词。在 Skip-Gram 中,会利用周围的词的预测结果来不断地调整中心词的词向量,最终所有的文本遍历完毕之后,也就得到了文本所有词的词向量。所以 Skip-Gram 进行预测的次数是要多于CBOW 的:因为每个词在作为中心词时,都要使用周围词进行预测一次。这样相当于比CBOW的方法多进行了K次(K 为窗口大小),因此时间的复杂度为O(KV),训练时间比CBOW 要长;
Word2Vec模型主要包含两种训练方法:
Negative sampling通过抽取负样本来定义目标
hierarchical softmax通过使用一个有效的树结构来计算所有词的概率来定义目标
二、算法设计 1.SVD构建词向量 基于SVD奇异值分解构建汉语子词向量的基本原理在前面已经介绍完毕,下面介绍如何进行算法设计。
1.1 数据集加载 首先是数据,本次实验主要用到了三个txt文件,分别是词表vocab.txt(来源于上⼀次构建的词表,以列表-字符串的形式存储,其长度为10000)
语料文件original.txt,该文件是第一次实验中的训练集和测试集的交集,一共31200条数据,部分内容如下
注意期望的语料应该是分词过后的语料,因此需要对original.txt使用jieba做分词处理,得到的corups.txt才是我们期望的语料
1 2 3 4 5 6 7 8 9 10 11 12 'original.txt' 'corups.txt' def preprocess_text ():with open (middle_file, 'r' , encoding='utf-8' ) as f_in, open (output_file, 'w' , encoding='utf-8' ) as f_out:for line in f_in:' ' .join(seg_list))
分词后的预料内容如下
pku_sim_test.txt测试文件,该文件源自网络,共500行数据,每行数据都是一组词对
准备好数据集后,依次构建函数读入词表、语料以及词对,下面三个函数非常简单也非常类似,借助python中的文件描述符对文件中的内容进行读取
1 2 3 4 5 6 7 8 9 def get_vocab (): with open ('vocab.txt' , 'r' ,encoding='utf-8' ) as f:for line in f.readlines():list (set (vocab)) print ("The number of the vocabulary: " , len (vocab))return vocab
1 2 3 4 5 6 7 8 9 def get_word_vector (): with open ('pku_sim_test.txt' , 'r' ) as f:for line in lines:print ("The length of the word vector: " , len (word_vec))return word_vec
1 2 3 4 5 6 7 8 9 def get_text (): with open ('corups.txt' , 'r' , encoding='utf-8' ) as f:for line in raw_lines: print ("The length of the text lines: " , len (text))return text
接着,需要从处理好的text语料中获取子词向量,前面介绍的时候说过,直接基于全文档的共现矩阵将耗费大量时间,因此此处选择窗口大小为5的滑动窗口来获取词对组合
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def get_subword_vector (text,window_size=5 ): for line in text:for i in range (len (line)-window_size+1 ): for j in range (i+1 ,i+window_size+1 ): if j <= len (line) -1 : if len (former) > 4 : 4 :] if len (latter) > 4 : 4 ]1 ] for x in subword_vec]print ("The length of the subword vector: " , len (subword_vec))return subword_vec
上述代码的基本思想是基于三层循环,第一层遍历语料、第二层遍历句子、第三层遍历单词,目的是通过迭代文本的每一行,在固定大小的窗口内创建所有可能的词对。
对于每一个词,函数会检查其长度是否大于4,如果是则将其截断,然后存储在subword_vec列表中(因为窗口大小固定为5).最后将所有子词向量的逆向量全部添加到subword_vec列表中,完成subword_vec的构建。
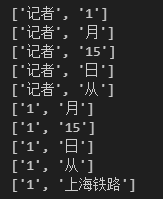
获取到的词对内容大致如下
1.2 共现矩阵构建 拥有了subword_vec后就可以创建并计算基于滑窗的共现矩阵了,基本思想就是在整个subword_vec上遍历并对出现过的子词进行计数操作
1 2 3 4 5 6 7 8 9 10 11 12 13 def Co_matrix (vocab, subword_vec ): len (vocab), len (vocab))) print ("Co_matrix is building..." )for i in tqdm(range (len (subword_vec))): try :0 ]][subword_vec[i][1 ]] += 1 except :pass print ("The shape of the co-occurrence matrix: " , M.shape)return M
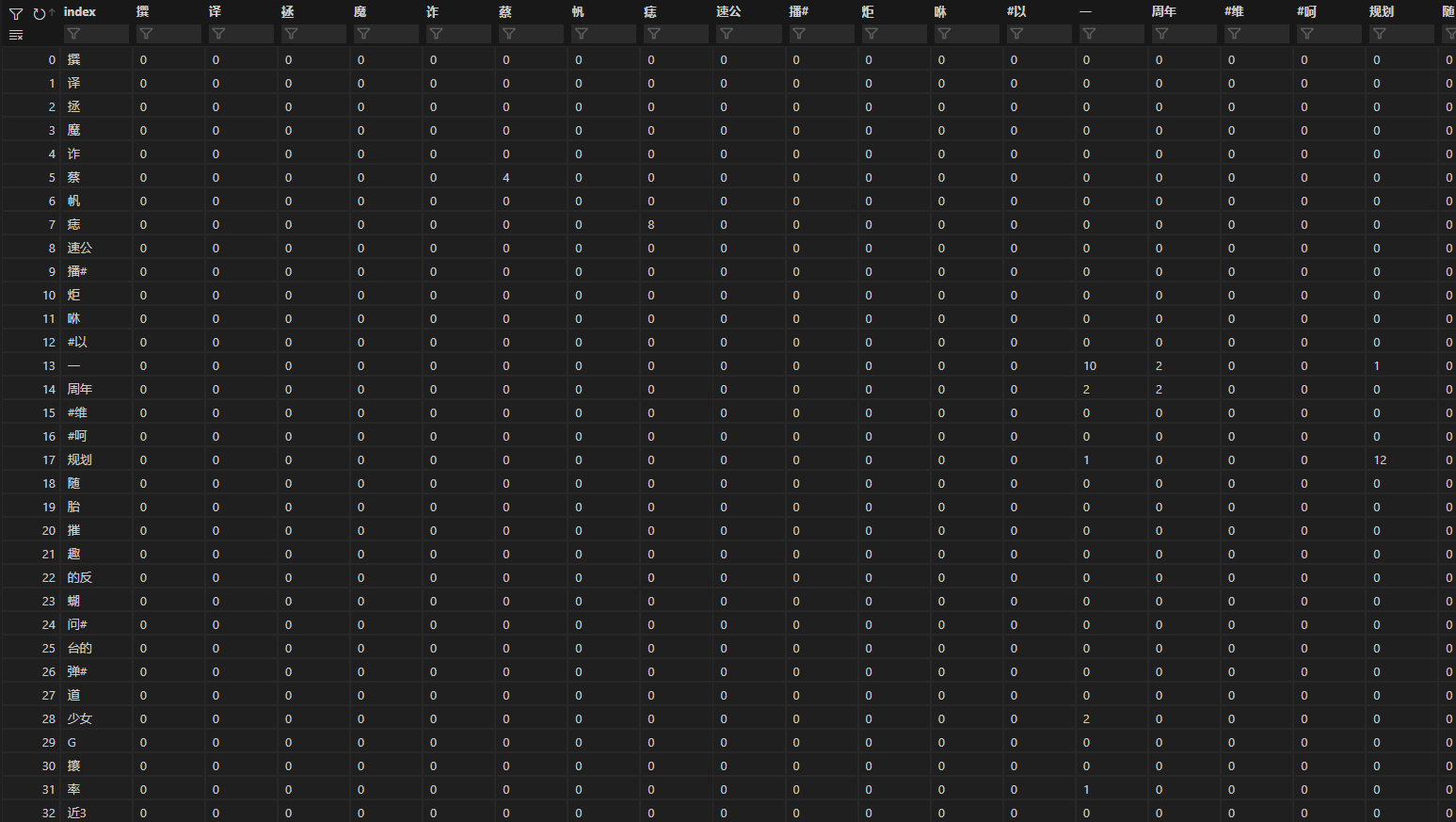
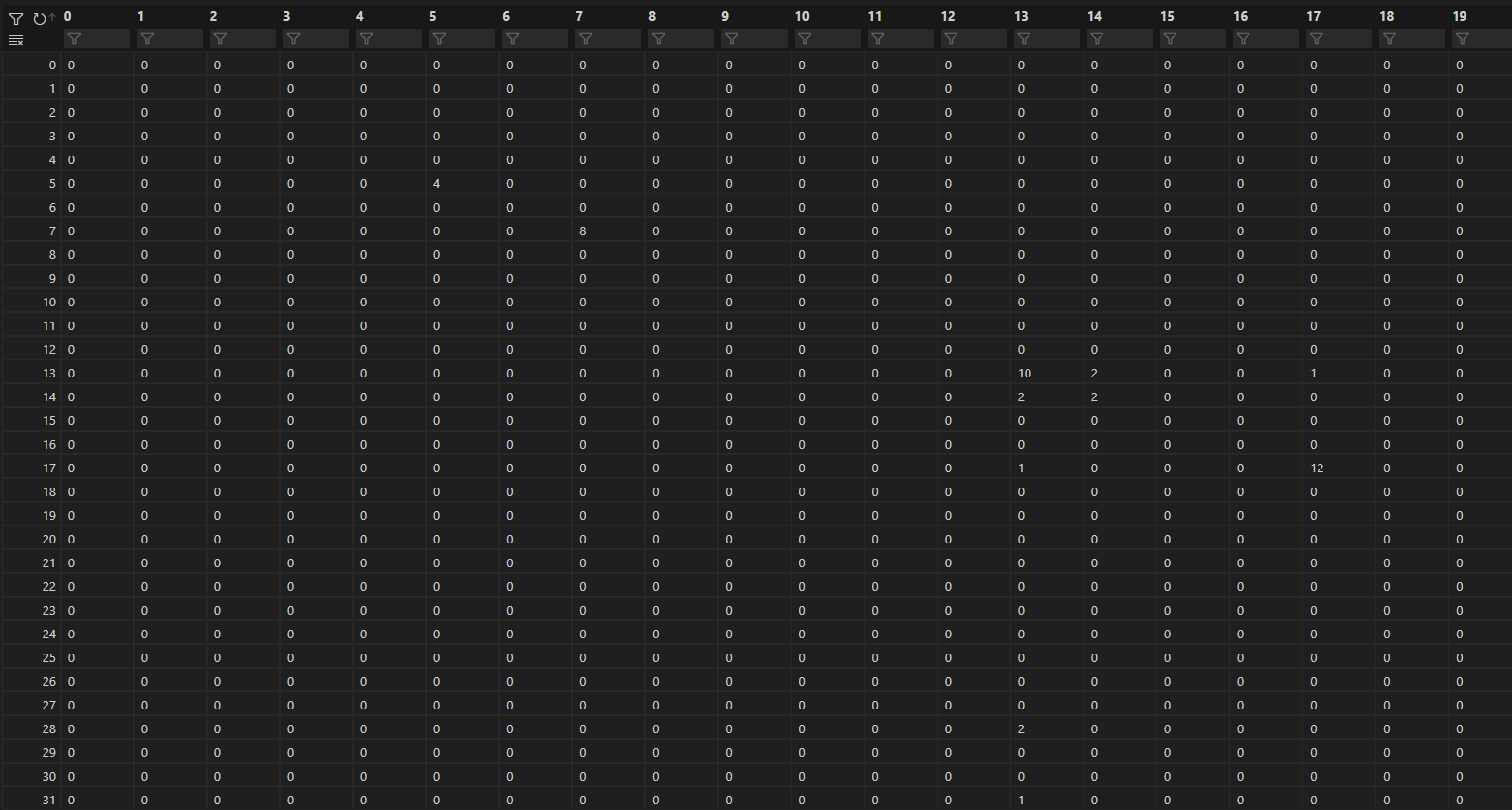
分别输出dataframe形式的df和numpy形式的M如下,这两个都是语料的共现矩阵,其中每个表格对应的数字就是该词对出现的次数(比如“一”“周年”为2表示“一周年”出现了两次)
1.3 奇异值分析 下面的任务是,对矩阵M进行奇异值分解,在进行分解之前,我们需要对其奇异值矩阵进行分析以选取合适的奇异值。
1 2 3 4 False )print ("singular_values: " , singular_values)print ("Number of singular values:" , len (singular_values))
借助numpy的linalg.svd方法可以对M矩阵计算,得到大小为10000的奇异值列表
借助numpy的count_nonzero方法对奇异值进行统计,最终得到9999个非0奇异值和1个0奇异值(也就是上面列表中最后的0值)
1 2 3 print ("Number of non-zero singular values:" , non_zero_singular_values)
可以看到这10000个奇异值按照从大到小的顺序进行排列,降维的本质就是选取列表中前k个奇异值作为SVD分解的奇异值个数,因为前k个值包含的重要信息较多,所以降维后对数据的影响较小。
那么应当如何选择合适的奇异值数量以用于SVD奇异值分解呢?
一种常见的方法是使用基于奇异值捕获的方差百分比(一种使用奇异值分解降维后保留多少信息的度量)的启发式方法。通过对每个奇异值进行平方并除以所有奇异值的平方和,可以计算每个奇异值所捕获的方差百分比。然后绘制这些百分比的累积总和,并选择一个阈值来捕捉所需的方差。通过检查每个奇异值捕获的方差百分比,可以确定需要多少个主成分(因此需要多少个特征)才能在数据集中保留总方差的一定百分比。这可以帮助选择适当数量的特征进行进一步分析,或者确定降维是否有效。
1 2 3 4 2 ) / (singular_values ** 2 ).sum ()
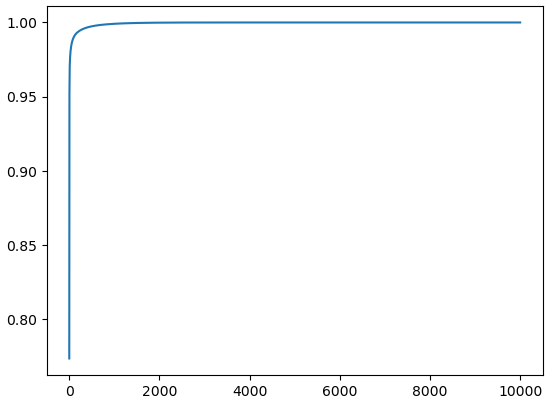
从上面这幅图也可以看到,前几个奇异值的平方占比相当大,因此我们只需要选择一个门限(此处设置为0.9)进行筛选即可得到需要选择的前k个(此处的输出为3)奇异值
1 2 3 4 0.90 1 print ("Number of singular values selected by variance_percentages:" , num_singular_values)
另一种方法是查看奇异值的累积和,并保留保留原始矩阵信息的一定百分比的奇异值的数量。例如,如果想保留90%的信息,则可以保留第一个“k”奇异值,使得第一个“k”奇异值的平方和除以所有奇异值的正方形和大于或等于0.9。而此处的积累和一般使用的是平方积累和而不是直接对奇异值求和,因为它提供了由奇异值捕获的数据的总方差的度量。奇异值的平方和也被称为矩阵“M*M.T”的迹,其中“M.T”表示矩阵“M”的转置。对奇异值进行平方强调较大奇异值的贡献,而淡化较小奇异值的影响。
1 2 3 4 5 6 7 2 )sum (singular_values**2 )0.90 )[0 ][0 ] + 1 print ("Number of singular values selected by energy_percentage:" , num_singular_values)
上面两种方法选择出的奇异值个数都为3,因此我们选择奇异值列表中的前3个奇异值[26545.73374919 8953.62252278 8152.45156942],分别计算它们的和以及与全体奇异值求和的比值
1 2 3 4 5 6 7 8 9 10 11 12 13 3 ]print ("Selected 3 singular values:" , selected_singular_values)sum (selected_singular_values)sum (singular_values)print ("Sum of selected singular values:" , selected_sum)print ("Sum of all singular values:" , total_sum)print ("Ratio of selected singular values to all singular values:" , ratio)
可能在这里有疑惑,明明前三个奇异值的累计和占比才百分之二十,为什么还要选择前三个?经过尝试,选取前1000个奇异值的累计和占比为82%,前2000个奇异值的累计和占比为91%,前3000个奇异值的累计和占比为98%,如果直接对奇异值求和来判断前k个奇异值的重要程度,并不能体现较大奇异值对矩阵的贡献。因此这里使用的是对前k个奇异值求平方后再求和,当这个和的占比大于90%时则选取这k个奇异值。
下面是选取的前三个奇异值的平方和以及占全体奇异值平方和的比率
1 2 3 4 5 6 7 8 9 sum (selected_singular_values**2 ) sum (singular_values**2 ) print ("Sum of selected singular values:" , selected_sum)print ("Sum of all singular values:" , total_sum)print ("Ratio of selected singular values to all singular values:" , ratio)
1.4 相似度计算 当确定选取的奇异值个数为3之后,借助sklearn.decomposition中的TruncatedSVD类,实例化一个svd对象后调用其fit_transform方法对矩阵M进行SVD降维。
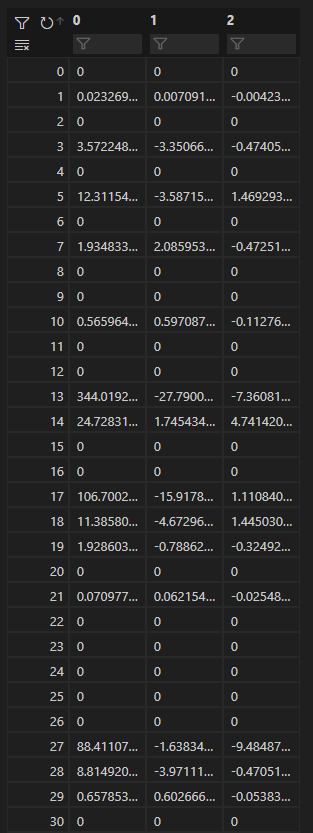
降维得到的result是一个10000*3的矩阵,其部分内容如下
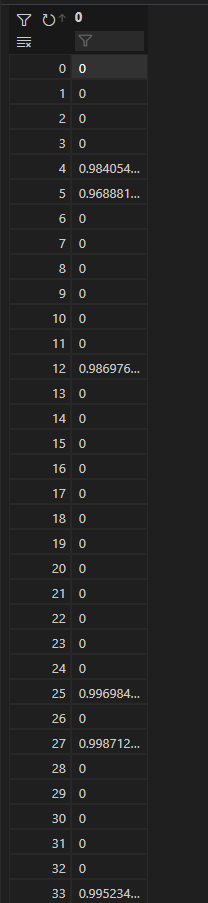
我们将基于该result矩阵对测试词对进行相似度计算。相似度计算有如下要求:基于子词向量计算pku_sim_test.txt中同一行中两个子词的余弦相似度sim_svd,当pku_sim_test.txt中某一个词没有获得向量时(该词未出现在该语料中),令其所在行的两个词之间的sim_svd=0。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 def similarity (M,n_components,word_vec,vocab ): for i in tqdm(range (len (word_vec))): if word_vec[i][0 ] in vocab and word_vec[i][1 ] in vocab: 0 ])] 1 ])]if frac2 != 0 : 4 ) else :0 else :0 ) return sim_svd
上述代码实现了对词对之间的余弦相似度的计算,其中sim_svd列表用于存储相似性得分。
对于word_vec中的每个词对,首先会检查这两个词是否都出现在vocab词表中,若任一一个没有出现则令其相似性得分为0。如果均存在则从vocab中获取词向量并计算其L2范数、点积和余弦相似度(最终结果保留至4位小数)。sim_svd变量是一个长度为500的列表,将其写入模型文件中保存。
2.SGNS构建词向量 初始词向量来源与original.txt文本使用jieba分词得到的corups.txt
1 2 3 4 5 6 7 8 9 def get_word_vector (): with open ('pku_sim_test.txt' , 'r' ) as f:for line in lines:print ("The length of the word vector: " , len (word_vec))return word_vec
借助gensim.models中的Word2Vec类可以轻松的初始化并训练一个Word2Vec模型
1 2 3 4 5 6 def train_model ():'corups.txt' ),100 , window=2 , sg=1 , hs=0 , min_count=1 ,workers=multiprocessing.cpu_count()) return vec_sgns
其参数如下
LineSentence(‘corups.txt’):模型的训练数据
vector_size=100:子词向量维度,即模型需要学习的词向量维度
window=2:窗口大小
sg=1:训练算法,此处表示使用skip-gram算法
hs=0:分层softmax使用的算法,此处表示不使用
min_count=1:一个单词必须出现在语料库中才能包含在词汇中的最小次数
workers=multiprocessing.cpu_count():CPU核并行加速处理
模型训练的日志输出如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 2023-05-07 17:17:48,492 - INFO - collecting all words and their countsINFO - PROGRESS: at sentence #0, processed 0 words, keeping 0 word typesINFO - PROGRESS: at sentence #10000, processed 487389 words, keeping 40636 word typesINFO - PROGRESS: at sentence #20000, processed 978125 words, keeping 61229 word typesINFO - PROGRESS: at sentence #30000, processed 1457089 words, keeping 75563 word typesINFO - collected 77491 word types from a corpus of 1514653 raw words and 31200 sentencesINFO - Creating a fresh vocabularyINFO - Word2Vec lifecycle event {'msg' : 'effective_min_count=1 retains 77491 unique words (100.00% of original 77491, drops 0)' , 'datetime' : '2023-05-07T17:17:49.275469' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'prepare_vocab' }INFO - Word2Vec lifecycle event {'msg' : 'effective_min_count=1 leaves 1514653 word corpus (100.00% of original 1514653, drops 0)' , 'datetime' : '2023-05-07T17:17:49.275469' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'prepare_vocab' }INFO - deleting the raw counts dictionary of 77491 itemsINFO - sample =0.001 downsamples 24 most-common wordsINFO - Word2Vec lifecycle event {'msg' : 'downsampling leaves estimated 1247291.7454936474 word corpus (82.3%% of prior 1514653)' , 'datetime' : '2023-05-07T17:17:49.709479' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'prepare_vocab' }INFO - estimated required memory for 77491 words and 100 dimensions: 100738300 bytesINFO - resetting layer weightsINFO - Word2Vec lifecycle event {'update' : False , 'trim_rule' : 'None' , 'datetime' : '2023-05-07T17:17:50.456679' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'build_vocab' }INFO - Word2Vec lifecycle event {'msg' : 'training model with 12 workers on 77491 vocabulary and 100 features, using sg=1 hs=0 sample=0.001 negative=5 window=2 shrink_windows=True' , 'datetime' : '2023-05-07T17:17:50.457677' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'train' }INFO - EPOCH 0 - PROGRESS: at 68.48% examples, 857957 words/s, in_qsize 0, out_qsize 0INFO - EPOCH 0: training on 1514653 raw words (1247127 effective words) took 1.4s, 860987 effective words/sINFO - EPOCH 1 - PROGRESS: at 63.43% examples, 789137 words/s, in_qsize 0, out_qsize 0INFO - EPOCH 1: training on 1514653 raw words (1247203 effective words) took 1.5s, 827498 effective words/sINFO - EPOCH 2 - PROGRESS: at 64.61% examples, 807510 words/s, in_qsize 0, out_qsize 0INFO - EPOCH 2: training on 1514653 raw words (1246960 effective words) took 1.5s, 817830 effective words/sINFO - EPOCH 3 - PROGRESS: at 62.11% examples, 774566 words/s, in_qsize 0, out_qsize 0INFO - EPOCH 3: training on 1514653 raw words (1247335 effective words) took 1.6s, 788682 effective words/sINFO - EPOCH 4 - PROGRESS: at 70.62% examples, 881039 words/s, in_qsize 0, out_qsize 0INFO - EPOCH 4: training on 1514653 raw words (1247370 effective words) took 1.4s, 874250 effective words/sINFO - Word2Vec lifecycle event {'msg' : 'training on 7573265 raw words (6235995 effective words) took 7.5s, 828414 effective words/s' , 'datetime' : '2023-05-07T17:17:57.986499' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'train' }INFO - Word2Vec lifecycle event {'params' : 'Word2Vec<vocab=77491, vector_size=100, alpha=0.025>' , 'datetime' : '2023-05-07T17:17:57.987496' , 'gensim' : '4.2.0' , 'python' : '3.7.16 (default, Jan 17 2023, 16:06:28) [MSC v.1916 64 bit (AMD64)]' , 'platform' : 'Windows-10-10.0.22000-SP0' , 'event' : 'created' }
模型一共进行了5轮训练,每次训练的batch大小为1514653个词,学习效率分别为
EPOCH 0:860987 effective words/s
EPOCH 1:827498 effective words/s
EPOCH 2:817830 effective words/s
EPOCH 3:788682 effective words/s
EPOCH 4:874250 effective words/s
模型训练完毕后,对待评测的词向量,调⽤vec_sgns.wv.similarity(word[0], word[1]),求取相似度
1 2 3 4 5 6 7 8 9 10 def similarity (word_vec,vec_sgns ):for word in tqdm(word_vec):try :0 ], word[1 ]), decimals=4 ) except :0 )return sim_sgns
待评测的词向量word_vec与SVD中使用的相同,即词对的列表,similarity方法计算词对之间的相似度。当pku_sim_test.txt中某一个词没有获得向量时(该词未出现在该语料中),令其所在行的两个词之间的sim_sgns=0,即异常处理sim_sgns.append(0),当词对均在语料中出现过则将相似度分数(保留4位小数)写入sim_sgns列表。sim_sgns变量是一个长度为500的列表,将其写入模型文件中保存。
3.结果输出 按照实验要求,将两种方法的结果汇总输出,要求如下:
输出文件命名方式:学号
所有输出文本均采用Unicode(UTF-8)编码
保持pku_sim_test.txt编码(utf-8)不变,保持原文行序不变;
每行在行末加一个tab符之后写入该行两个词的sim_svd,再加一个tab符之后写入该行两个词的sim_sgns;
1 2 3 4 5 6 7 8 9 10 11 12 def summary_result (word_vec ):with open ('2020212183.txt' ,'w' ,encoding='utf-8' ) as f:with open ('sim_svd.txt' , 'r' ) as f1:with open ('sim_sgns.txt' , 'r' ) as f2:float (sim_svd[i].strip()) for i in range (len (sim_svd))]float (sim_sgns[i].strip()) for i in range (len (sim_sgns))]for i in range (500 ):str (' ' .join(word_vec[i])) + ' ' + str (sim_svd[i]) + ' ' + str (sim_sgns[i]) + '\n' )
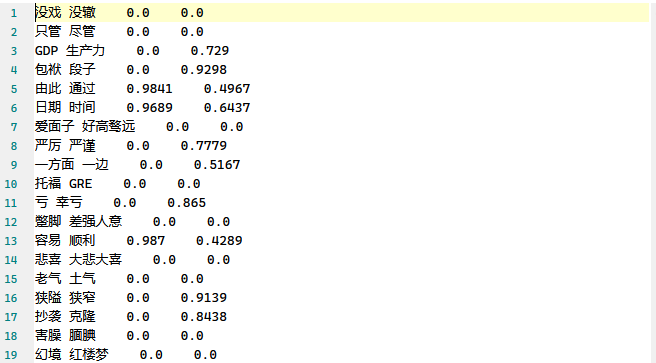
最终的相似度输出文件部分内容如下,第一个数值表示两个词的sim_svd,第二个数值表示两个词的sim_sgns
三、实验总结 本次实验分别基于SVD矩阵分解和SGNS两种方法对汉语子词构建向量,同时利用构建的向量评测词对之间的相似度。
对SVD能够应用于自然语言处理我刚开始还是很意外的,后来在深入了解了SVD的原理后明白了SVD用于构建词向量的基本原理,同时也了解了另一种构建词向量的方式 – Word2Vec,这种方式包含两种不同的模型,其中一种就是本次实验需要使用的Skip gram模型,基于负采样的方案能够很快速的使得模型训练收敛。
经过本次实验再次加深了我对自然语言处理课程知识点的掌握程度,同时辨析明确了很多易混概念,最重要的一点是将课程所学内容用代码实现出来,使所学内容能够真正应用到实际。
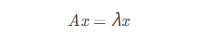
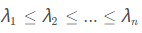 以及这n个特征值对应的特征向量
以及这n个特征值对应的特征向量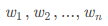 ,则矩阵A可以被特征分解为下面的表示
,则矩阵A可以被特征分解为下面的表示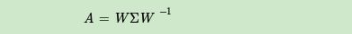
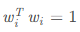 ,此时这n个标准化后的特征向量被称为标准正交基,此时的W方阵满足
,此时这n个标准化后的特征向量被称为标准正交基,此时的W方阵满足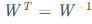 (在实数域上我们称其转置等于其逆的矩阵为正交矩阵)。因此矩阵A的特征分解表达式还可以写作
(在实数域上我们称其转置等于其逆的矩阵为正交矩阵)。因此矩阵A的特征分解表达式还可以写作