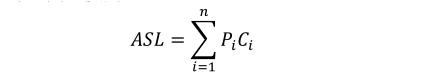考研_专业课_知识点汇总

2023/8/1 20:16 本篇博客主要整理考研数据结构中需要着重背诵且的基本数据结构和算法相关代码，由C和C++语言构成。关于这些算法的解释在另一篇笔记中非常详细，这里尽量给出简洁可背的代码，不让整个笔记看起来杂糅。

另外，这里给的代码也并不是说万精油（没有哪个数据结构给的资料可以说是完全适用，毕竟数据结构是应用学科），更多的是需要我们去理解其内部核心思想（比如顺序表的删除的实质就是移动元素）并学习代码写作风格，这样遇到由特定要求的题目不至于一筹莫展。

额外的还给出了某些常用算法的时间复杂度分析(对于某些简单的算法不给出时间复杂度)，一方面加深对算法的理解，另一方面保证在解题的时候可以直接背诵使用。

2023/9/12 20:38 本来想的是把这个博客写成纯代码博客，但是随着后面学习的深入，这篇博客开始总结越来越多的除代码外其他必背考点。所以这里稍微做一个转型，之后也把刷题总结以及另一个数据结构上面的重要内容移到这个博客中，相比于之前那个博客这篇更加精简适合背诵 – 初学新知识还是整理到之前那个文档(专业课_数据结构)中，那个文档并不是不使用，而是不作为背诵的材料；

---

一、线性表

1.基本数据结构定义

1.1 顺序表结构体定义

因为一维数组可以是静态分配也可以是动态分配，所以顺序表结构体定义也有两种（ElemType表示任意元素类型，天勤习惯使用int，王道习惯使用ElemType）

#define maxSize 100
typedef struct Sqlist{
    int data[maxSize];
    int length;
}Sqlist; // 静态数组

typedef struct Sqlist{
    int *data; // ElemType *data;
    int maxSize,length;
}Sqlist； // 动态数组

1.2 单链表结点定义

typedef struct LNode{
    int data;
    struct LNode *next;
}LNode;

1.3 双链表结点定义

typedef struct DLNode{
    int data;
    struct DLNode *prior;
    struct DLnode *next;
}DLNode;

1.4 静态链表定义

与顺序表相同，静态链表也需要预先分配一块连续的内存空间，静态链表以next==-1作为结束标志

#define maxSize 50
typedef struct Slinklist{
    Elemtype data; // 数据域
    int next; // 指针域
}Slinklist;
Slinklist[maxSize]; // 结构体数组，数组中的每个元素都是上述定义的Slinklist结构体

静态链表的插入、删除操作与单链表相同，只需要修改指针不需要移动元素

2.顺序表的基本操作

2.1 初始化

void initList(Sqlist &L){
    L.length = 0;
}

2.2 按位查找

int getElem(Sqlist L,int p,int &e){
    if(p<0 || p>L.length-1)
        return 0; // 查找失败
    e = L.data[p];
    return 1; //查找成功
}

顺序表具有随机存储特性，因此其按值查找的时间复杂度为O(1)

2.3 按值查找

int findElem(Sqlist L, int e){
    for(int i=0;i<L.length;i++){
        if(e==L.data[i])
            return i; // 查找成功返回下标
    }
    return 0； // 查找失败
}

最好情况：查找元素就在表头，只需要比较一次，时间复杂度为O(1)

最坏情况：查找元素在表尾或不存在，比较n次，时间复杂度为O(n)

平均情况：平均比较次数为(n+1)/2，时间复杂度为O(n)

2.4 插入元素

int insertElem(Sqlist &L;int p;int e){
    if(p<0 || p>L.length || L.length == maxSize)
        return 0; //插入失败
    for(int i=L.length-1;i>=p;i--)
        L.data[i+1]=L.data[i];
    L.data[p]=e;
    ++(L.length);
    return 1;
}

最好情况：表尾插入，元素不用后移，时间复杂度为O(1)

最坏情况：表头插入，元素后移语句执行n次，时间复杂度为O(n)

平均情况：平均移动次数为n/2，时间复杂度为O(n)

2.5 删除元素

int deleteElem(Sqlist &L,int p,int &e){
    if(p<0 || p>L.length-1)
        return 0;
    e = L.data[p]; // 保存删除元素
    for(int i=p;i<=L.length-2;i++)
        L.data[i]=L.data[i+1]; // 覆盖以达到删除的目的
    --(L.length);
    return 1;
}

最好情况：删除表尾元素，时间复杂度为O(1)

最坏情况：删除表头元素，移动除表头元素外的所有元素，时间复杂度为O(n)

平均情况：平均移动次数为(n-1)/2，时间复杂度为O(n)

3.单链表的基本操作

3.1 尾插法

void creatlistR(LNode *&C,int a[],int n){ // 利用数组a中的n个元素建立不含头结点的单链表C
    LNode *s,*r;
	C=(LNode *)malloc(sizeof(LNode)); // 申请头指针C指向的头结点空间
    C->next=NULL;
    r=C; 
    // 链表初始化完成，开始尾插法
    for(int i=0;i<n;i++){
        s=(LNode *)malloc(sizeof(LNode)); // S指向新申请的结点
        s->data=a[i];
        // 尾插法（只需要接头）
        r->next=s; // 将新结点接入链表尾部
        r=r->next; // r始终指向终端结点，这句写为 r=s; 等价
    }
    r->next = NULL;
}

尾插法生成的链表中结点的次序和输入数据的顺序一致，因为有尾指针r的存在因此时间复杂度为n*O(1)=O(n)

3.2 头插法

void createlistF(L Node *&C,int a[],int n){
    LNode *s;
    C=(LNode *)malloc(sizeof(LNode)); // 申请头指针C指向的头结点空间
    C->next=NULL;
    // 初始化完成开始头插法
    for(int i=0;i<n;i++){
        s=(LNode *)malloc(sizeof(LNode)); // S指向新申请的结点
        s->data=a[i];
        // 头插法（先接屁股再接头）
        s->next = C->next;
        C->next = s;
    }
}

头插法建立单链表时，读入数据的顺序与生成的链表中的元素的顺序是相反的。每个结点的插入时间为O(1)，因此长度为n的单链表的建表时间复杂度为O(n)

3.3 按序查找

int GetElem(LNode *C,int i){
    if(i<1)
        return NULL;
    LNode *p = C->next; // 头结点指向的下一个结点（第一个结点）
    int j = 1;
    while(p!=NULL && j<i){
        p=p->next;
        j++; // 计数器
    }
    return p;
}

按序查找的时间复杂度显然为O(n)（没有说明具体什么复杂度的时候统一认为是最坏时间复杂度）

3.4 按值查找

int findElem(LNode *C,int x){
	LNode *p = C->next; // 从开始结点开始比较
    while(p!=NULL && p->data!=e){
        p=p->next;
    }
    return p;
}

很明显按值查找的时间复杂度为O(n)

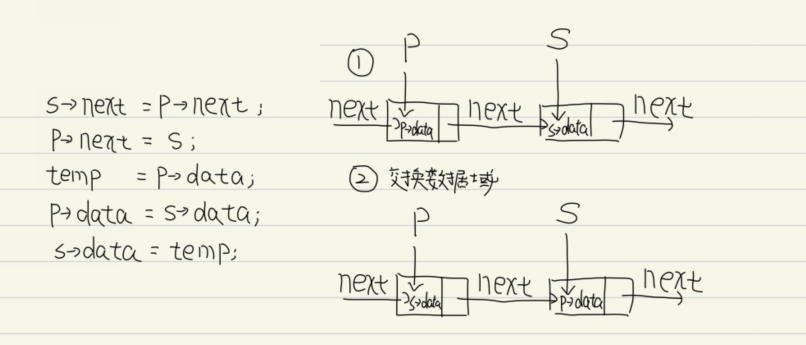
3.5 插入元素

3.5.1 后插操作

核心是找到插入结点的前一个结点，所以需要首先调用按序查找，再执行下面的代码片段

s->next = p->next;
p->next = s;

算法的主要时间开销在查找元素，时间复杂度为O(n)，若直接给定结点在后面插入新结点则时间复杂度为O(1)

3.5.2 前插操作

任何前插操作都可以转换为后插操作，但后插操作时间复杂度为O(n)，下面这种方式实现了以时间复杂度为O(1)的方式进行前插操作

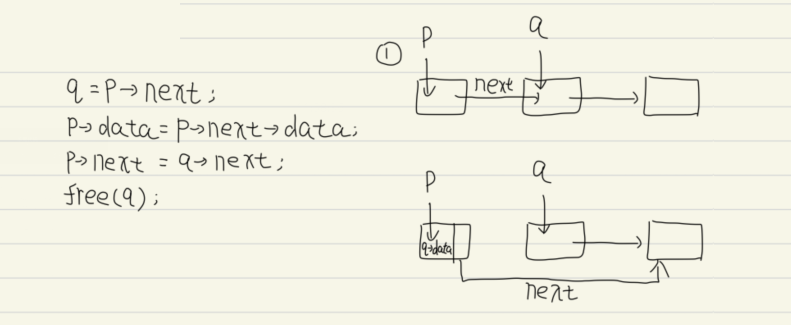
3.6 删除元素

核心是找到被删除结点的前一个结点，与插入操作相同需要先使用按序查找，然后执行下面代码

q=p->next;
p->next = p->next->next;
free(q);

因此其时间复杂度同样为O(n)，但是，删除结点还有一种时间复杂度为O(1)的算法，本质上就是将其后继节点的值赋予本身然后删除后继节点

4.双链表的基本操作

双链表在单链表的结点中增加了一个指向其前驱的prior指针，因此双链表中的按值查找和按序查找与单链表相同，但双链表在插入和删除操作的实现上与单链表有较大的不同。因为双链表可以很方便的找到其前驱结点，因此双链表的插入、删除操作的时间复杂度仅为O(1)

4.1 尾插法

void createDlistR(DLNode *&L,int a[],int n){
    DLNode *s,*r; // s指向新申请的结点，r始终指向终端结点
    L=(DLNode *)malloc(sizeof(DLNode));
    L->prior = NULL;
    L->next = NULL;
    r=L;
    // 初始化完成，开始尾插法
    for(int i=0;i<n;i++){
        s = (DLNode *)malloc(sizeof(DLNode));
        s->data = a[i];
        // 尾插法
        r->next = s; //两条链互相链接才算作接入双链表
        s->prior = r;
        r=s;
    }
    r->next = NULL;
}

4.2 插入元素

在p结点后插入s结点

s->next = p->next;
s->prior = p;
p->next = s;
s->next->prior =s;

4.3 删除元素

删除p结点后的q结点

q = p->next; // q指向被删除结点
//先将要被删除的结点的两端链子处理
p->next = q->next;
q->next->prior = p;
free(q); // 删除结点

二、栈和队列

1.基本数据结构定义

1.1 顺序栈结构体定义

typedef struct sqStack{
    int data[maxSize]; // 存放栈中元素
    int top; // 栈顶指针
}sqStack;

1.2 链栈结点定义

typedef struct LNode{
    int data; // 数据域
    struct LNode *next; // 指针域
}LNode;

1.3 顺序队列结构体定义

typedef struct sqQueue{
    int data[maxSize];
    int front; // 队首指针
    int rear; // 队尾指针
}sqQueue;

1.4 链队列结点定义

队结点类型定义

typedef struct QNode{
    int data; // 数据域
    struct QNode *next; // 指针域
}QNode;

链队类型定义

typedef struct LiQueue{
    QNode *front; // 队头指针
    QNode *rear; // 队尾指针
}LiQueue;

2.顺序栈的基本操作

顺序栈的基本图示结构如下

2.1 初始化

初始化操作的实质就是将栈顶指针置为-1

void initStack(sqStack &st){
    st.top = -1;
}

2.2 判空操作

int isEmpty(sqStack st){
    if(st.top == -1)
        return 1; // 栈空
    else
        return 0; // 栈非空
}

2.3 进栈操作

进栈操作可以简写为stack[++top]=x;，其时间复杂度为O(1)

int push(sqStack &st,int x){ // 将元素x入栈
    if(st.top == maxSize-1) // 栈满不能入栈
        return 0;
    ++(st.top); // 先移动指针再进栈
    st.data[st.top] = x;
    return 1;
}

2.4 出栈操作

出栈操作可以简写为x=stack[top--];，其时间复杂度为O(1)

int pop(sqStack &st,int &x){
    if(st.top == -1) // 栈空不能出栈
        return 0;
    x = st.data[st.top]; // 保留出栈元素的副本
    --(st.top); // 先取出元素再移动指针
    return 1;
}

3.链栈的基本操作

链栈的基本图示结构如下

3.1 初始化

void initStack(LNode *&lst){
    lst = (LNode *)malloc(sizeof(LNode));
    lst->next = NULL; // 申请并初始化头结点
}

3.2 判空操作

int isEmpty(LNode *lst){
    if(lst->next == NULL)
        return 1; //空
    else 
        return 0; //非空
}

3.3 进栈操作

链栈的入栈和出栈时间复杂度同样为O(1)

void push(LNode *lst,int x){
    LNode *p = malloc(LNode *)malloc(sizeof(LNode));
    p->next = NULL; // 申请新结点并初始化器指针域为空（这是一个好习惯）
    //头插法进栈
    p->dada = x;
    p->next = lst->next;
    lst->next = p;
}

3.4 出栈操作

出栈一般需要将出栈元素保存在x中

int pop(LNode *lst,int &x){
    if(lst->next == NULL) //栈空不能出栈
        return 0;
    // 出栈实质就是单链表的删除操作
    LNode *p=lst->next;
    x=p->data;
    lst->next = p->next;
    free(p);
    return 1;
}

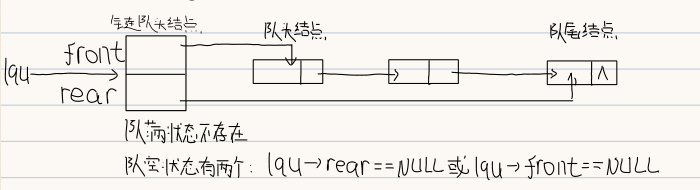
4.顺序队列的基本操作

因为顺序队列存在“假溢出”的情况，所以实际使用意义不大，一般都选择使用循环队列替代。循环队列的基本图示如下

4.1 初始化

void initQueue(sqQueue &qu){
    qu.front = qu.rear = 0; //栈空且首尾指针均指向0
}

4.2 判空操作

int isQueueEmpty(sqQueue qu){
    if(qu.front == qu.rear)
        return 1; //栈空
    else
        return 0; // 非空
}

4.3 进队操作

int enQueue(SqQueue &qu,int x){
    if((qu.rear+1)%maxSize == qu.front) // 队满不能入队
        return 0;
    qu.rear = (qu,rear+1)%maxSize; // 先移指针再取元素
    qu.data[qu.rear] = x;
    return 1;
}

4.4 出队操作

int deQueue(sqQueue &qu,int &x){
    if(qu.front == qu.rear) // 栈空不能出队
        return 0;
    qu.front = (qu.front+1)%maxSize; // 先移指针再取元素
    x=qu.data[qu.front];
    return 1;
}

5.链队的基本操作

5.1 初始化

void initQueue(LiQueue *&lqu){
    lqu=(LiQueue *)malloc(sizeof(LiQueue)); //创建头结点并将链表置空
    lqu->front = lqu->rear = NULL;
}

5.2 判空操作

int isQueueEmpty(LiQueue *lqu){
    if(lqu->rear == NULL ||qu->front == NULL)
        return 1; // 任一为NULL则表空；
    else
        return 0;
}

5.3 入队算法

void enQueue(LiQueue *lqu,int x){
    QNode *p = (QNode *)malloc(sizeof(QNode));
    p->datax = x;
    p->next = NULL; // 结点p待插入
    if(lqu->rear == NULL||lqu->front == NULL)
        lqu->rear=lqu->next=p; //若待插入队列为空，则新结点既是队首结点也是队尾结点
    else
        lqu->rear->next=p; //新结点从队尾入队
    lqu->rear=p； //rear尾指针始终指向队尾结点
}

5.4 出队操作

int deQueue(LiQueue *lqu,int &x){
    if(lqu->next==NULL||lqu->front==NULL) //队空不能出队
        return 0;
    else
        p=lqu->front;//队首元素出队
    if(lqu->front==lqu->rear)
        lqy->front=lqu->rear=NULL; //若队列中只有一个元素出队，出队后成为空队列
    else
        lqu->front=lqu->front->next;
    x=p->data; //保存出队元素副本
    free(p);
    return 1;
}

三、串

1.基本数据结构定义

串的两种最基本的存储方式是链式存储和顺序存储，但一般情况下使用的都是顺序存储，顺序存储分为堆存储(变长顺序存储)和数组存储(定长顺序存储)

1.1 定长顺序存储结构体

typedef struct Str{
    char str[maxSize+1]; //数组长度比串长度多1是为了存储结束标记'\0'
    int length;
}Str;

1.2 变长顺序存储结构体

变长存储表示方法有顺序存储结构的有点，同时操作中串的长度可以根据需要来进行设定更加灵活，因此更加常用，其形象的表示如下

其代码表示如下

typedef struct Str{ 
    char *ch; //指向动态分配存储区域首地址的字符指针
    int length; //串长度
}Str;

2.串的基本操作

2.1 赋值操作

赋值操作的本质是数组赋值

int strassign(Str &str,char *ch){ //其中str是待赋值字符串，ch是常量字符串
    if(str.ch) //清空待赋值字符串，使其指向空字符数组
        free(str.ch);
    int len = 0 ; //统计字符个数
    char *c = ch; //接收常量字符串
    while(*c){ //计算常量字符串的长度，此处的计算结果不包含结束标记（因为while循环到结束标记'\0'时会直接退出循环）
        ++len;
        ++c;
    }
    
    if(len == 0){ //若常量字符串为空则直接赋值为空串
        str.length = 0;
        str.ch = NULL;
        return 1; //赋值成功标记
    }
    else{ //此处需要申请len+1长度的空间，后面赋值的时候无论是否显式赋值'\0'编译器都会自动添加
        str.ch = (char *)malloc(sizeof(char)*(len+1));
        if(str.ch == NULL)
            return 0; //申请连续空间失败，赋值失败
        else{
            c = ch;
            for(int i=0;i<=len;i++,c++){
                str.ch[i]=*c;//逐一赋值
            }
            str.length = len; // 字符串的长度不包括结束标记，这与前面计算的长度不冲突
            return 1;
        }
    }
}

2.2 取串长操作

int strlength(Str str){
    return str.length;
}

2.3 串比较操作

int strcompare(Str s1,Str s2){
    for(int i=0;i<s1.length && i<s2.length;i++){
        if(s1.ch[i]!=s2.ch[i]) //若两字符相等则比较下一位置的字符大小
            return s1.ch[i]-s2.ch[i]; //ASCLL直接相减可以得到大小信息
    }
    return s1.length-s2.length； //若前缀都相同则先结束为较小串
}

2.4 串连接操作

int contact(Str &str,Str str1,Str str2){ // 将str1和str2首尾相连合并为一个串
    if(str.ch){
        free(str.ch);
        str.ch = NULL; //释放原空间并重定向
    }
    str.ch=(char *)malloc(sizeof(char)*(str1.length+str2.length+1));
    if(str.ch == NULL)
        return 0; //若两个串均为空串则直接返回
    while(int i<str1.length){
        str.ch[i]=str1.ch[i];
        ++i;
    }
    while(int j<=str2.length){ //此处将str2的结束标记一同复制，相当于手动添加
        str.ch[i+j]=str2.ch[j];
        ++j;
    }
    str.length=str1.length+str2.length;
    return 1;
}

2.5 求子串操作

int substring(Str &substr,Str str,int pos,int len){ //求母串str中从pos位置开始长度为len的子串substr
    if(pos<0 || pos>=str.length || len<0 || len>str.length-pos) // 母串中的字符存储在[0.length-1]的位置，这些均为非法状态
        return 0;
    if(substr.ch){
        free(substr.ch); //先释放内存避免内存泄漏
        substr.ch=NULL; //再置空指针避免悬挂
    }
    if(len = 0){ //子串为空串
        substr.ch = NULL;
        substr.length=0;
        return 1;
    }
    else{
        substr.ch = (char*)malloc(sizeof(char)*(len+1));
        int i =pos;
        int j=0;
        while(i<pos+len){
            sunstr.ch[j]=str.ch[i];
            ++i;
            ++j;
        }
        substr.ch[j] = '\0'; //手动添加结束标记
        substr.length = len;
        return 1;
    }
}

2.6 串清空操作

int clearstr(Str &str){
    if(str.ch){
        free(str.ch);
        str.ch=NULL;
    }
    str.length=0;
    return 1;
}

3.串的模式匹配

这里为了理解的方便，串中对应的字符对应下标1~length而非前面数组存储中的0~length-1

3.1 朴素模式匹配

int BF(Str str,Str substr){
    int i=1,j=1,k=1;//串字符的起始下标为1，k用于记录主串回溯的位置
    while(i<=str.length&&j<=substr.length){
        if(str.ch[i]==substr.ch[j]){
            ++i;
            ++j;//若匹配成功则继续匹配下一个字符
        }
        else{ //匹配失败则子串和主串均进行回溯操作
            j=1; //j回到子串的开始位置
            k=k+1;
            i=k；//i回到主串的下一位置
        }
    }
    if(j>substr.length)
        return k; //匹配成功则返回子串在主串中的起始位置
    else 
        return 0; //匹配失败
}

假设主串长度为n模式串长度为m，并且进行多次匹配后匹配成功

• 最好情况：每一趟匹配时比较的第一个字符不同，平均比较次数为(n+m)/2，一般n远大于m故时间复杂度为O(n)
• 最坏情况：每一趟匹配比较到最后一个字符时两字符不同，平均比较次数为(n-m+2)*m/2，时间复杂度为O(nm)

如果匹配失败按照匹配成功的最坏情况分析，时间复杂度为O(nm)

3.2 KMP模式匹配

3.2.1 KMP匹配算法

KMP实际就是基于朴素模式匹配的改进，所以在代码风格上与之类似

int KMP(Str str,Str substr,int next[]){
    int 1=1,j=1; 
    while(i<=str.length&&j<=substr.length){
        if(j==0 || str.ch[i]=substr.ch[j]){
            ++j;
            ++i;
        }
        else
            j=next[j]; //主串中的i无需回溯，只需要回溯j到对应的next数组指向的位置
    }
    if(j>substr.length)
        return i-substr.length;
    else 
        return 0;
}

• 代码中的j==0的理解只是一种正确性上的理解，实际上j==0那一句的作用是当主串的第i个位置和模式串的第一个字符不匹配的时候，从主串的i+1个位置开始匹配；
• KMP算法的时间复杂度为O(n+m)

3.2.2 next数组构造*

next数组的构造仅依赖模式串，这部分内容网上几乎没有讲的很直观的视频，这里我给出最权威也最简单的算法描述：前缀和后缀进行比较，如果前缀和后缀没有相同前缀，则为0+1，如果相同，则相同的字符个数+1。下面是一个标准的next数组的构造示例

序号j: 1 2 3 4 5 6 7 8 9 10 11 12
模式串s: a b a b a a a b a b  a  a
next[]: 0 1

 1.next[1],next[2]无论是什么模式串数组，永远都是0和1。
 
 2.next[3]：如上，序号j[3]对应的模式串s[3]，那么我们就看模式串s[3]前面的字符即可，即为a b,那么s[3]的前缀为a,后缀为b,a和b不相同,则next[3]为0+1=1;
 
 3.next[4]:序号j[4]对应的s[4],找s[4]的前面字符，为a b a,字符前缀为a、ab；后缀为ba, a;有1个相同字符，则next[4]=1+1=2;

 4.next[5]:序号j[5]对应的s[5],找s[5]的前面字符，为a b a b,字符前缀为a、ab、aba三个，后缀为bab、ab、b三个，进行比较，有字符串ab相同，则next[5]=2+1=3

 以此类推......

 5.next[12]:序号j[12]对应的模式串字符为s[12],取前n-1个字符，为a b a b a a a b a b a,前缀为：ababaaabab、ababaaaba...后缀为babaaababa、abaaababa...可看出前缀中 ababa与后缀中ababa5个字符相同，则next[12]=5+1=6;

最终生成的next字符串为
j: 1 2 3 4 5 6 7 8 9 10 11 12
s: a b a b a a a b a b  a  a
next: 0 1 1 2 3 4 2 2 3 4  5  6 （next数组的值对应了每个位置的最长相同前缀和后缀的长度）

上述算法描述对应的代码如下

void getnext(Str substr,int next[]){ //该代码非常难理解但是写的非常好（天勤视频KMP讲的非常差不推荐）
    int i=1,j=0; //默认首字符从数组下标1开始
    next[1]=0; //next数组第一个元素总是0
    while(i<substr.length){ // 该循环遍历子串，构建next数组
        if(j==0 || substr.ch[i] == substr.ch[j]){ // 如果j==0或当前字符等于前缀字符，则表示找到一个匹配的前缀
            ++j;
            ++i;
            next[i]=j;
        }
        else{ // 若不匹配，则将j设置为next[j]，目的是找到更短的前缀（从最长的开始找，没有就退求其次找短一点的前缀）
            j=next[j];
        }
    }
}

为了更进一步理解代码，这里结合上述例子对next数组构造

1.初始化 i=1 和 j=0，并设置 next[1]=0
2.进入循环，比较 substr.ch[i] 和 substr.ch[j]，即 s[1] 和 s[0]，它们分别是字符 "a" 和 "a"。因为它们相等，所以执行以下操作：
	增加 i 和 j，现在 i=2 和 j=1
	设置 next[2] 为 j，即 next[2] = 1
3.比较 s[2] 和 s[1]，即字符 "a" 和 "b"，它们不相等。这时候执行 else 分支，将 j 设置为 next[j]，即 j 变成 1
4.比较 s[2] 和 s[1]，仍然不相等。继续执行 else 分支，将 j 设置为 next[j]，这时 j 变成 0
5.比较 s[2] 和 s[0]，即字符 "a" 和 "a"，它们相等。因此，执行以下操作：
	增加 i 和 j，现在 i=3 和 j=1
	设置 next[3] 为 j，即 next[3] = 1

3.2.3 nextval数组构造*

nextval数组可以看作是对next数组的改进，在使用时直接将KMP算法重点的next数组换为nextval数组即可。同样这里分别介绍手动求解nextval数组和代码实现nextval数组，手动求解的算法思想如下：

• 若对应字符不同，直接填入next的值；
• 若对应字符相同，填入该值对应的序号的next的值

  序号 : 1 2 3 4 5 6 7 8 9 10 11 12
模式串s: a b a b a a a b a b  a  a
 next[]: 0 1 1 2 3 4 2 2 3 4  5  6
nextval: 0 

1.nextval[1]=0,默认值
2.nextval[2]：s[2]对应的next值为1，则以1为下标s[1]=a,与s[2b进行对比,不相同，则将s[2]对应的next值直接下发到nextval，nextval[2]=next[2]=1;
3.nextval[3]：s[3]对应的next值为1，则以1为下标，与s[3]=a进行对比，相同，则nextval[3]=nextval[1]=0;
4.nextval[4]：s[4]对应的next值为2,则以2为下标,与s[4]=b进行对比，相同，则nextval[4]=nextval[1]=0;
5.依次同理.....
6.nextval[12]:s[12]对应的next值为6，则s[6]=a与s[12]=a对比,相同，则nextval[12]=nextal[6]=4;

最终生成的nextval为：
  序号 : 1 2 3 4 5 6 7 8 9 10 11 12
模式串s: a b a b a a a b a b  a  a
 next[]: 0 1 1 2 3 4 2 2 3 4  5  6
nextval: 0 1 0 1 0 4 2 1 0 1  0  4

下面是代码实现（实在理解不了就硬背，这部分几乎不会考代码几乎都是手动计算。花费大量时间记忆不是一个明智的选择）

void getnextval(Str substr,int nextval[]){ //本代码直接求解naxtval数组而不借助next计算
    int i=1,j=0;
    nextval[1]=0;
    while(i<substr.length){
        if(j==0 || substr.ch[i]==substr.ch[j]){
            ++j;
            ++i;
            if(substr.ch[i]!=substrch[j])
                nextval[i]=j; //对应字符不同则nextval[]=next[]
            else
                nextval[i]=nextval[j]; //对应字符相同则nextval[]=nextval[]
        }
        else
            j=nextval[j];
    }
}

四、矩阵

1.矩阵的定义

# define m 4
#define n 5
int A[m][n]; //二维数组存储矩阵，其中m和n必须是常量

2.矩阵的转置

void trsmat(int A[][maxSize],int B[][maxSize],int m,int n){ //矩阵A和B的大小统一设置为maxSize*maxSize，而m和n是实际矩阵的大小
    for(int i=0;i<m;i++){ //矩阵的行、列下标均从0开始
        for(int j=0;j<n;j++)
            B[j][i]=A[i][j];
    }
}

3.矩阵相加

void addmat(int C[][maxSize],int A[][maxSize],int B[][maxSize],int m,int n){
    for(int i=0;i<m;i++){
        for（int j=0;j<n;j++）{
            C[i][j]=A[i][j]+B[i][j];
        }
    }
}

4.矩阵相乘

void mutmat(int C[][maxSize],int A[][maxSize],int B[][maxSize],int m,int n,int k){ //矩阵A大小为m*n，B大小为n*k，A*B=C大小为m*k
    for(int i=0;i<m;i++){
        for(int j=0;j<k;j++){
            C[i][j]=0;
            for(int h=0;h<n;h++)
                C[i][j]+=A[i][h]*B[h][j];
        }
    }
}

五、树和二叉树

1.基本数据结构定义

1.1 二叉链表结点定义

二叉树的顺序存储结构不便于存储任意形态的二叉树（顺序结构一般存储完全二叉树），更常使用二叉链表存储

typedef struct BTNode{
    char data;
    struct BTNode *lchild;
    struct BTNode *rchild;
}BTnode;

1.2 线索二叉树结点定义

typedef struct TBTNode{
    char data; //数据域
    int ltag,rtag; //线索标记
    struct TBTNode *lchild;
    struct TBTNode *rchild;
}TBTNode;

其中ltag和rtag是标识域：

• ltag=0表示lchild为指针指向结点的左孩子；ltag=1表示lchild为线索指向结点的直接前驱；
• rtag=0表示rchild为指针指向结点的右孩子；rtag=1表示rchild为线索指向结点的直接后继；

1.3 并查集定义

#define SIZE 13
int UFSet[SIZE]; //并查集可以直接使用int型数组表示

2.二叉树的遍历

二叉树的深度优先包括前、中、后序三种遍历方式，广度优先即指层序优先遍历

无论是哪种遍历方式，每个结点都访问一次且仅访问一次，故时间复杂度均为O(n)

2.1 前序遍历

2.1.1 前序遍历的递归实现

void preoder(BTNode *p){ //二叉树的前序遍历也可以认为是深度优先遍历
    if(p!=NULL){
        // 中左右
        visit(p);
        preorder(p->lchild);
        preorder(p->rchild);
    }
}

2.1.2 前序遍历非递归实现

前、中、后序的非递归实现都是使用自定义的栈来替代系统栈

void preorderNonrecursion(BTNode *bt){
    if(bt != NULL){
        BTNode *Stack[maxSize]; //自定义栈以代替系统栈
        int top=-1; //初始化栈
        BTNode *p;
        Stack[++top]=bt; //根结点入栈
        while(top != -1){ //栈非空则持续进行前序遍历
            p=Stack[top--]; //输出栈顶结点
            visit(p);
            if(p->rchild != NULL) //若栈顶结点的右孩子存在则入栈（先入后出）
                Stack[++top]=p->rchild;
            if(p->lchild != NULL)
                Stack[++top]=p->lchild;
        }
    }
}

2.2 中序遍历

2.2.1 中序遍历递归实现

void inoder(BTNode *p){ 
    if(p!=NULL){
        // 左中右
        inorder(p->lchild);
        visit(p);
        inorder(p->rchild);
    }
}

2.2.2 中序遍历非递归实现

中序非递归遍历的执行步骤如下：

1. 根结点入栈；
2. 循环执行：若栈顶结点左孩子存在，则左孩子入栈；若栈顶结点左孩子不存在，则出栈并输出栈顶结点，再检查其右孩子是否存在，若存在则右孩子入栈；
3. 栈空时结束算法；

基本算法思想为：使用了一个栈来模拟递归过程，首先向左遍历树的最深的左子树，然后出栈并访问节点，然后再转向右子树

void inorderNoncursion(BTNode *bt){
    if(bt != NULL){
        BTNode *Stack[maxSize];
        int top=-1; //初始化栈空
        BTNode *p =bt; //初始化p指针指向根结点
        while(top !=-1 || p!=NULL){ //中序遍历，栈空并不一定遍历结束。循环条件为栈非空或者当前节点指针不为空
            while(p!=NULL){ // 迭代向左走到最深的左子树
                Stack[++top]=p;  // 将当前节点入栈
                p=p->lchild; // 移动到左子节点
            }
            if(top!=-1){ //如果栈非空
                p=Stack[top--]; // 弹出栈顶节点，并赋值给p
                visit(p); // 访问当前节点
                p=p->rchild; // 将p移动到右子节点，继续中序遍历右子树
            }
            
        }
    }
}

2.3 后序遍历

2.3.1 后序遍历递归实现

void postoder(BTNode *p){
    if(p!=NULL){
        // 左右中
        postorder(p->lchild);
        postorder(p->rchild);
        visit(p);
    }
}

2.3.2 后序遍历非递归实现

后序遍历的非递归实现可以看作是如下两个步骤的结果：

1. 将先序遍历的左右子树遍历顺序交换得到逆后序遍历序列；
2. 对逆后序遍历序列进行逆序操作得到后序遍历序列；

// 该代码是最高难度级别
void postorderNonrecursion(BTNode *bt){
    if(bt != NULL){
        //定义两个栈，一个用于逆后序，一个用于逆序
        BTNode *Stack1[maxSize];int top1 =-1;
        BTNode *Stack2[maxSize];int top2 =-1;
        BTNode *p=NULL;
        Stack1[++top1]=bt; //根结点入栈1
        while(top1!=-1){ //栈1非空则持续遍历
            p=Stack1[top1--]; //输出栈1栈顶结点
            Stack2[++top2]=p; //输入栈2（栈2进行visit操作，先入后出）
            if(p->lchild != NULL)
                Stack1[++top1]=p->lchild;
            if(p->rchild != NULL)
                Stack1[++top1]=p->rchild;
        }
        while(top2!=-1){ //出栈顺序即为后序遍历顺序
            p=Stack2[top2--];
            visit(p);
        }
    }
}

2.4 层序遍历

层序遍历借助一个循环队列实现。先将头结点入队，然后出队，对该结点执行访问操作

• 若该结点有左子树，则将左子树的根结点入队
• 若该结点有右子树，则将右子树的根结点入队

然后出队，继续对出队的结点进行访问

void level(BTNode *p){ //非递归实现的广度优先遍历
    //借助循环队列实现
    int front,rear;
    BTNode *que[maxSize]; //初始化循环队列
    front=rear=0;
    BTNode *q; //注意不是p指针而是q指针，q指针用于指向出队的队头结点，p指针指向待遍历的二叉树根结点
    if(p!=NULL){
        rear=(rear+1)%maxSize;
        que[rear]=p; //根结点入队
        while(front != rear){ //队列非空则循环，进行层序遍历
            front=(front+1)%maxSize; 
            q=que[front]; //队头结点出队
            visit(q);
            //检查出队结点
            if(q->lchild != NULL){
                rear=(rea+1)%maxSize;
                que[rear]=q->lchild;
            }
            if(q->rchild != NULL){
                rear=(rear+1)%maxSize;
                que[rear]=q->rchild;
            }
        }
    }
}

3.线索二叉树的遍历

线索二叉树的意义在于，二叉树被线索化后近似一个线性结构，分支结构的遍历操作因此转换为近似线性结构的遍历操作，通过线索的辅助使得寻找当前结点的前驱或后继的平均效率大大提高。

3.1 中序线索二叉树

3.1.1 线索化

基本思想很简单，即采用二叉树中序递归遍历算法，在遍历过程中连接上合适的线索即可。当整颗二叉树遍历完成，线索化也随之完成

1. 左线索指针指向当前结点在中序遍历序列中的前驱结点
2. 右线索指针指向后继结点

void CreateInThread(TBTNode *root){
    TBTNode *pre = NULL;
    if(root != NULL){
        InThread(root,pre);
        //处理中序最后一个结点
        pre->rchild=NULL; 
        pre->rtag=1;
    }
}

其中的核心函数InThread如下

void InThread(TBTNode *p,TBTNode *&pre){ //p指针指向当前访问的结点，pre指向p的前驱结点
	if(p!=NULL){
        //1.遍历左子树
        InThread(p->lchild,pre); //递归，对左子树进行线索化
        //2.遍历中子树（核心，建立线索）
        if(p->lchild==NULL){ //左孩子为空表示左线索存在，建立当前结点的左/前驱线索
            p->lchild=pre;
            p->tag=1;
        }
        if(pre!=NULL && pre->child==NULL){ //右孩子为空则右线索存在，建立前驱结点的右/后继线索
            pre->rchild=p;
            pre->tag=1;
        }
        pre=p; //结点跟踪，保证pre始终指向p的前驱结点
        //3.遍历右子树
        InThread(p->rchild,pre); //递归，右子树线索化
    }
}

3.1.2 遍历

中序线索二叉树的结点中隐含了线索二叉树的前驱和后继信息。在对其进行遍历时，只要先找到序列中的第一个结点，然后依次找结点的后继，直至其后继为空。

在中序线索二叉树中找结点后继的规律是：若其右标志为“1”，则右链为线索，指示其后继，否则遍历右子树中第一个访问的结点（右子树中最左下的结点）为其后继。

void Inorder(TBTNode *root){ //中序线索遍历
    for(TBTNode *p=First(root);p!=NULL;p=Next(p)){ //First(root)表示以root为根的中序第一个结点，Next(p)表示p的后继节点
        visit(p);
    }
}

TBTNode *First(TBTNode *p){ //中序遍历的第一个结点就是整棵树最左的结点
    while(p->ltag==0)
        p=p->lchild; //一直访问结点的左孩子
    return p;
}

TBTNode *Next(TBTNode *p){
    if(p->rtag==0)
        return First(p->rchild); //寻找以p->rchild为根的中序第一个结点（即当前结点的后继结点）
    else
        return p->rchild; //rtag==1则rchild直接指向后继结点
}

3.2 前序线索二叉树

3.2.1 线索化

代码结构与中序线索化相似，区别在于将连接线索的代码提前到两个递归入口的前面。

void preThread(TBTNode *p,TBTNode *&pre){
    if(p!=NULL){
        if(p->lchild==NULL){
            p->lchild=pre;
            p->tag=1;
        }
        if(pre!=NULL && pre->rchild==NULL){
            pre->rchild=p;
            pre->tag=1;
        }
        pre=p;
        // 递归入口的条件要求左/右指针不是线索才能继续递归（原因未知）
        if(p->ltag==0){
            prethread(p->lchild,pre);
        }
        if(p->rchild==0){
            prethread(p->rchild,pre);
        }
    }
}

3.2.2 遍历

void preorder(TBTNode *root){
    if(root!=NULL){
        TBTNode *p=root;
        while(p!=NULL){
            while(p->ltag==0){ //左指针不是线索，边访问边左移
                visit(p);
                p=p->lchild;
            }
            visit(p); //此时p左指针必定为线索，访问之
            p=p->rchild; //此时p的的左孩子不存在，若右指针非空，则无论其是否是线索都直接指向后继
        }
    }
}

3.3 后序线索二叉树

3.3.1 线索化

代码结构与中序线索化相似，区别在于将连接线索的代码放到两递归入口的后面。

void postThread(TBTNode *p,TBTNode *&pre){
    if(p!=NULL){
        prethread(p->lchild,pre);
        prethread(p->rchild,pre);
        
        if(p->lchild==NULL){
            p->lchild=pre;
            p->tag=1;
        }
        if(pre!=NULL && pre->rchild==NULL){
            pre->rchild=p;
            pre->tag=1;
        }
        pre=p;
    }
}

4.并查集的基本操作

4.1 初始化

void initial(int S[]){
    for(int i=0;i<SIZE;i++)
        S[i]=-1; //并查集元素全部初始化为-1
}

4.2 原始操作

4.2.1 原始查找

该函数返回x所属的根结点，时间复杂度为O(n)（即树的高度）

int Find(int S[],int x){
    while(S[x]>0)
        x=S[x];
    return x;
}

4.2.2 原始合并

无论是原始还是优化后的合并操作的时间复杂度均为O(1)，主要影响的是查找操作的时间复杂度

void Union(int S[],int Root1,int Root2){
    if(Root1==Root2)
        return; //不同的集合才能进行合并
    S[Root2]=Root1; //修改集合2的父结点为集合1
}

若要合并两个非根结点，则先使用Find找到对应的根结点后，再对两个根结点执行Union操作

4.3 优化操作

4.3.1 优化合并

使得树高不超过[logn]+1，使Find操作的复杂度降低为O(logn)

void Union(int S[],int Root1,int Root2){
    if(Root1==Root2)
        return;
    if(S[Root2]>S[Root1]){ //根结点的绝对值表示树的结点总数，小树合并到大树
        S[Root1]+=S[Root2];
        S[Root2]=Root1;
    }
    else{
        S[Root2]+=S[Root1];
        S[Root1]=Root2;
    }
}

4.3.2 优化查找(压缩路径)

压缩路径后，Find操作的时间复杂度低于O(logn)（甚至可能为常数级别）

int Find(int S[],int x){ //将压缩路径操作与Find操作结合，边查找边进行压缩（为下一次查找作优化）
    int root=x;
    while(S[root]>=0)
        root=S[root]; //一直往上找到根结点
    while(x!=root){ //压缩路径，将路径上所有的结点都挂载到根结点下
        int t=S[x];
        S[x]=root; //将x挂在到root下
        x=t; //向上找根
    }
    return root;
}

六、图

1.基本数据结构定义

1.1 邻接矩阵定义

邻接矩阵是图的顺序存储结构

typedef struct Vertextype{ //顶点类型
    int no; //顶点编号
    char info; //顶点信息
}VertexType;

typedef struct MGraph{ //邻接矩阵
    int edges[maxSize][maxSize]; //边的标识
    int n,e; //n为顶点数，e为边数
    VertexType vex[maxSize]; //顶点信息
}MGraph;

1.2 邻接表定义

邻接表是图的链式存储结构，由顶点表和边表两部分组成

1. 顶点表结点存储顶点信息和指向第一个边表结点的指针
2. 边表结点存储与当前顶点邻接的顶点序号以及指向下一边表结点的指针

typedef struct ArcNode{ //边表结点
    int adjvex; //与当前顶点邻接的顶点序号
    struct ArcNode *nextarc; //指向下一个边表结点
    int info; //边的信息（如权值）
}ArcNode;

typedef struct VNode{ //顶点表结点
    char data; //顶点信息
    ArcNode *firstarc; //指向边表第一个结点
}VNode;

typedef struct AGraph{ //邻接表
    VNode adjlist[maxSize];
    int n,e; //顶点数和边数
}AGragh;

2.图的遍历

2.1 深度优先(DFS)

图的深度优先类似二叉树的先序遍历。二叉树的先序遍历对每个结点需要递归访问两个分支，图的深度优先需要递归访问多个分支。

算法执行过程如下：

1. 任取一个顶点访问；
2. 检查这个顶点的所有邻接顶点，递归访问其中未被访问的顶点

以邻接表为存储结构的DFS如下

int visit[maxSize]; //visit数组作为顶点访问标记
void DFS(AGragh *G,int v){ // v是第一个被访问的结点
    ArcNode *p; //边表指针用于指向边
    visit[v]=1; //修改标记
    visit(v);
    p=G->adjlist[v].firstarc; //顶点v的第一条边
    while(p!=NULL){ //检查顶点v的所有邻接顶点
        if(visit[p->adjvex]==0)
            DFS(G,p->adjvex); //递归访问未被访问的顶点
        p=p->nextarc; //若被访问过则p指向v的下一条边
    }
}

2.2 广度优先(BFS)

图的广度优先类似树的层序遍历，同样需要借助队列实现。算法执行流程如下：

1. 任取图中一个顶点访问，将该顶点入队并标记为已访问；
2. 队列非空时执行遍历循环：出队，依次检查出队顶点的所有邻接顶点，访问没有被访问过的邻接顶点并将其入队；
3. 队列空时跳出循环表示遍历完成；

以邻接表为存储结构的广度优先搜索算法如下

void BFS(AGraph *G,int v,int visit[maxSize]){
    ArcNode *p;
    int que[maxSize].front=0,rear=0; //队列的简单定义
    int j;
    visit(v);
    visit[v]=1;
    rear=(rear+1)%maxSize; //当前顶点v入队
    que[rear]=v;
    while(front!=rear){ //队列为空则遍历完成
        front=(front+1)%maxSize; //顶点出队
        j=que[front]; //依次检查出队顶点的所有邻接顶点
        p=G->adjlist[j].firstarc; //p指向顶点第一条边
        while(p!=NULL){ //选取与顶点邻接的全部顶点
            if(visit[p->adjvex]==0){ //访问未被访问的邻接顶点并将其入队
                visit(p->adjvex);
                visit[p->adjvex]=1;
                rear=(rear+1)%maxSize;
                que[rear]=p->adjvex;
            }
            p=p->nextarc; //p指向顶点下一条边
        }
    }
}

2.3 非连通图的遍历

上述遍历代码针对的是连通图，针对非连通图直接暴力遍历每个顶点即可

2.3.1 深度优先

void dfs(AGrapg *g){
    for(int i=0;i<g->n;i++){
        if(visit[i]==0)
            DFS(g,i);
    }
}

2.3.2 广度优先

void bfs(AGraph *g){
    for(int i=0;i<g->n;i++){
        if(visit[i]==0)
            BFS(g,i,visit);
    }
}

3.最小生成树

普里姆和克鲁斯卡尔算法都是针对无向图的最小生成树算法

3.1 普里姆算法

从树中某个顶点v0开始，构造生成树的算法执行过程如下：

1. 将v0到其他顶点的所有边作为候选边；
2. 重复以下步骤n-1次使得其他n-1个顶点被归入树中：
   1. 从候选边中挑选出权值最小的边输出，并将与该边另一端相连的顶点v并入树中；
   2. 考察所有甚于顶点vi，若(v,vi)的权值比lowcost[vi]小则更新该值

以邻接矩阵为图的存储结构的普里姆算法如下

void Prim(MGraph g,int v0,int &sum){
    int lowcost[maxSize],vset[maxSize],v; //lowcost指示当前生成树到剩余各顶点的最短边权值，vset指示是否入树
    int i,j,k,min;
    v=v0; //v0是树根
    for(i=0;i<g.n;i++){ //初始化
        lowcost[i]=g.edges[v0][i]; //将v0到其他顶点的边的权值作为lowcost的值
        vset[i]=0; //此时没有顶点被归入树种
    }
    vset[v0]=1; //将树根并入生成树中
    sum 0; //sum用于积累计算树的权值
    for(i=0;i<g.n-1;i++){ //重复以下步骤n-1次使得剩余的n-1个顶点归入生成树中
        min=INF; //无穷大常量
        for(j=0;j<g.n;j++){ //选出侯选边中的最小者并将其另一邻接顶点归入生成树中
            if(vset[j]==0 && lowcost[j]<min){
                min=lowcost[j]; //更新最小值
                k=j;
            }
        }
        vset[k]=1;
        v=k;
        sum+=min; //sum计算最小生成树的权值
        for(j=0;j<g.n;j++){
            if(vset[j]==0 && g.edges[v][j]<lowcost[j])
                lowcost[j]=g.edges[v][j]; //更新lowcost值
        }
    }
}

该算法的核心部分是双重循环，因此该算法的时间复杂度为O(n^2^)

3.2 克鲁斯卡尔算法

算法思想非常直接：每次找出侯选边中权值最小的边，将该边并入生成树中，重复该操作直到所有边都被检测完

typedef struct Road{ //该数组用于存放图中的边以及顶点信息
    int a,b; //边的两个顶点
    int w; //边的权值
}Road;

void KrusKal(MGraph g,int &sum,Road road[],int v[]){ //其中数组v是并查集数组
    int N=g.n; //图的顶点数
    int E=g.e; //图的边数
    sum=0; //生成树权值
    for(int i=0;i<E;i++)
        v[i]=-1; //初始化并查集
    sort(road,E); //对road数组中的E条边按权值从小打到进行排序
    for(int i=0;i<E;i++){ //从最小边开始扫描
        int a=Find(road[i].a);
        int b=Find(road[i].b);
        if(a!=b){ //若该边不构成回路，即两个顶点不再同一个并查集中
            v[a]=b; //将a集合并入b集合
            sum=road[i].w;
        }
    }
}

算法的时间花费主要在sort和单层循环，更一般的，克鲁斯卡尔算法的时间复杂度由所选取的排序算法决定。排序算法处理的数据规模由图的边数决定，与图的顶点数无关，该算法适用于稀疏图。

4.最短路径

以下两个算法均针对有向图的最短路径

4.1 迪杰斯特拉算法

该算法需要三个辅助数组：

• dist[vi]表示从源顶点到vi的最短路径长度
• path[vi]表示从源顶点到vi的最短路径上vi的前一个结点
• set[vi]标记了顶点vi是否已经被归入最短路径中

该算法的执行流程如下：

1. 从当前dist[]数组中选出最小值并将该顶点vu的set设置为1；
2. 以vu为中间顶点更新源顶点到剩余未被归入的顶点的路径长度；
3. 对1、2执行n-1次得到源顶点到其余n-1个结点的最短路径；

void Dijstra(MGraph g,int v,int dist[],int path[]){ //其中v是起点，dist数组存放v到vi的最短路径，path存放v到vi最短路径上vi的前一个顶点
    int set[maxSize]; //标记数组，指示结点是否被归入最短路径
    for(int i=0;i<g.n;i++){ //初始化操作
        dist[i]=g.edges[v][i];
        set[i]=0;
        if(g.edges[v][i]<INF)
	        path[i]=v;
        else
        	path[i]=-1;
    }
    set[v]=-1;
    path[v]=-1;
    //初始化结束，执行n-1次循环并入剩余结点
    for(int i=0;i<g.n-1;i++){
        int min=INF;
        for(int j=0;i<g.n;j++){ //从剩余结点中选出路径最短的结点
            if(set[j]==0 && dist[j]<min){
                int u=j;
                min=dist[j];
            }
        }
        set[u]=1; //将该结点并入最短路径中
        for(int j=0;i<g.n;j++){ //以该结点为中转更新所有路径
            if(set[j]==0&&dist[u]+g.edges[u][j]<dist[j]){
                dist[j]=dist[u]+g.egdes[u][j];
                path[j]=u;
            }
        }
    }
}

因为是嵌套双层循环，所以可以得出时间复杂度为O(n^2^)

利用path数组可以输出源顶点到目标顶点的路径，借助栈实现

void printfPath(int path[],int a){ //a是目标结点
    int stack[maxSize],top=-1; //栈实现由根到叶的逆向输出
    while(path[a]!=-1){
        stack[++top]=a;
        a=path[a];
    }
    stack[++top]=a;
    while(top!=-1)
        cout<<stack[top--]<<" ";
}

4.2 弗洛伊德算法

迪杰斯特拉是求解图中某一顶点到其他顶点的最短路径，弗洛伊德可以求解图中任意两个顶点之间的最短路径（并且算法更加简单，只是时间复杂度较高）

需要使用两个辅助数组：

• A用于记录当前任意两个顶点最短路径的长度
• Path用于记录当前两个顶点最短路径上的中间顶点

算法流程如下：

1. 初始化两个矩阵，将图的邻接矩阵赋值给A，将Path中的所有元素设置为-1；
2. 以顶点k为中间顶点，对图中所有顶点对的路径进行更新；

void Floyd(MGraph *g;int path[][maxSize],int A[][maxSize]){ //其中path保存两个顶点最短路径的中间结点，A保存两顶点间最短路径长度
    for(int i=0;i<g->n;i++){ //初始化辅助数组
        for(int j=0;j<g->n;j++){ 
            A[i][j]=g->edges[i][j];
            path[i][j]=-1;
        }
    }
    for(int k=0;k<g->n;k++){ //以k为中间结点，检测所有顶点对
        for(int i=0;i<g->n;i++){
            for(int j=0;j<g->n;j++){
                if(A[i][j]>A[i][k]+A[k][j]){
                    A[i][j]=A[i][k]+A[k][j];
                    path[i][j]=k;
                }
            }
        }
    }
}

因为主要部分是三层循环，故该算法的时间复杂度为O(n^3^)

借助矩阵A和矩阵Path可以输出任意两个顶点间的最短路径序列

void printPath(int u,int v,int path[][maxSize],int A[][maxSize]){ //其中u是源结点，v是目标结点
    if(A[u][v]==INF)
        return; //无路径直接结束
    else{
        if(path[u][v]==-1)
            输出边<u,v>
        else{
            int mid=path[u][v];
            printPath(u,mid,path,A);
            printPath(mid,v,path,A);
        }
    }
}

5.拓扑排序

5.1 顺拓扑排序

在一个有向图无环图中找到拓扑排序的基本流程如下：

1. 从有向图中找到入度为0的顶点输出；
2. 删除1中的顶点以及从该顶点出发的全部边；
3. 重复上述两步直到图中不存在入度为0的点；

int topSort(AGraph *G){
    int i,j,n=0;
    int stack[maxSize].top=-1; //栈容器
    ArcNode *p;
    for(i=0;i<G->n;i++){ //将度为0的顶点入栈
        if(G->adjlist[i].count==0)
            stack[++top]=1; 
    }
    while(top!=-1){ //拓扑排序
        i=stack[top--];
        ++n; //记录输出顶点个数
        cout<<i<<" "; //入度为0的顶点出栈（等效于删除该顶点）
        p=G->adjlist[i].firstarc; //遍历出栈顶点的所有边并找到邻接点，删边并修改count的值
        while(p!=NULL){
            j=p->adjvex;
            --(G->adjlist[j].count);
            if(G->adjlist[j].count==0) 
                stack[++top]=j; //入度为0则入栈待输出
            p=p->nextarc;
        }
    }
    if(n==G->n)
        return 1;
    else
        return 0;
}

5.2 逆拓扑排序

在一个有向图无环图中找到逆拓扑排序的基本流程如下：

1. 从有向图中找到出度为0的顶点输出；
2. 删除1中的顶点以及到达该顶点的全部边；
3. 重复上述两步直到图中不存在出度为0的点；

逆拓扑排序可以借鉴顺拓扑排序的算法思想，但更常考的是利用深度优先实现逆拓扑排序，只需要修改深度优先代码中的Visit(v);代码段的位置即可

int visit[maxSize];
void DFS(AGraph *G,int v){
    ArcNode *p;
    visit[v]=1;
    p=G->adjlist[v].firstarc;
    while(p!=NULL){
        if(visit[p->adjvex]==0)
            DFS(G,p->adjvex);
        p=p->nextarc;
    }
    visit(v);
}

七、内部排序

若没有特殊说明，本章所有排序算法都默认是非递减排序。

1.插入类排序

1.1 直接插入排序

算法思想：每趟排序都将一个待排序的关键字按照其大小插入到有序序列的适当位置，直到所有待排序关键字都被插入到有序序列中

void InsertSort(int R[],int n){ //待排关键字n个，全部存储在数组R中
    int temp;
    for(int i=1;i<n;i++){ //外层循环对无序序列从左向右逐个排序，因为第一个关键字下标为0，可直接视为第一个关键字有序
        temp = R[i]; //将待排关键字存储在temp临时变量中
        for(int j=i-1;j>=0&&temp<R[j];j--){ //i是无序序列的第一个元素，i-1是有序序列最后一个元素，内层循环从右到左扫描，将更大的关键字逐个后移
            R[j+1]=R[j]; //逐个移动，无序的第一个元素j+1因此会被覆盖成为有序
        }
        R[j+1]=temp; //插入到第一个比待排关键字小的有序关键字后面
    }
}

时间复杂度分析：

• 最坏情况：整个序列为逆序，基本操作总执行次数为n(n-1)/2，时间复杂度为O(n^2^)

• 最好情况：整个序列有序，内层循环始终不执行，时间复杂度为O(n)

• 平均情况：时间复杂度为O(n^2^)

空间复杂度分析：算法所需辅助空间不随无序序列的规模变化而变化（常量），故空间复杂度为O(1)

1.2 折半插入排序

折半插入排序算法是对直接插入排序算法的一种改进，它通过减少比较次数来提高排序的效率。这个算法与直接插入排序算法的不同之处在于，在寻找插入位置时使用了二分查找，这样可以减少比较的次数，从而提高了排序的效率。在实际应用中，折半插入排序通常比直接插入排序更快，特别是对于大型数据集

void BinaryInsertSort(int R[],int n){
    int i,j,low,high,mid,temp;
    for(int i=1;i<n;i++){
        temp=R[i];
        low=0;
        hign=i-1;
        while(low<=high){ //折半查找待插入位置，最终的low所指就是插入位置
            mid=(low+high)/2;
            if(temp<R[mid])
                high=mid-1;
            else
                low=mid+1;
        }
        for(j=i-1;j>=low;j--){ //逐个后移
            R[j+1]=R[j];
        }
        R[low]=temp;
    }
}

时间复杂度分析：

• 最好情况：O(nlogn)
• 最坏情况：O(n^2^)
• 平均情况：O(n^2^)

空间复杂度仍然为O(1)

1.3 希尔排序

希尔排序又称为缩小增量排序，是对直接插入排序的一种改进（直接插入排序适用于序列基本有序的情况）。希尔排序的每趟排序都会使得序列整体更加有序，减少了元素的移动次数提升效率。

其代码类比直接插入排序，相当接近

void ShellInsert(int arr[],int n){ //此代码是对天勤原有代码的修改，旨在方便记忆，当gap=1时即为直接插入排序的代码
    int temp;
    for(int gap=n/2;gap>0;gap/=2){ //增量常常取n/2
        for(int i=gap;i<n;i++){ //gap前的关键字是第一个关键字，视为有序序列，而gap指向无序序列第一个元素
            temp=arr[i];
            for(int j=i-gap;j>=0&&temp<arr[j];j-=gap){ //与直接插入排序对比记忆
                arr[j+gap]=arr[j]; // 逐个后移，无序第一个关键字j+gap会被覆盖成为有序
            }
            arr[j+gap]=temp;
        }
    }
}

希尔排序的时间复杂度和增量的选取相关（无论怎么选，增量的最后一个值一定取1）：

• 增量从n/2开始，每次都除以2向下取整，此时时间复杂度为O(n^2^)；
• 另一种情况是选取增量为2^k^+1<=n，此时时间复杂度为O(n^1.5^)；

希尔排序的空间复杂度为O(1)

2.交换类排序

2.1 起泡排序

每趟起泡排序都会使得无序序列中最大的关键字被交换到最后，起泡排序算法的结束条件是在一趟排序过程中没有发生关键字的交换

void BubbleSort(int R[],int n){ 
    int i,j,flag;
    int temp;
    for(i=n-1;i>=1;i--){ //i从1开始是为了确保最后一趟R[0]与R[1]做比较。外层循环指示当前无序序列的范围
        flag=0; // 标记本趟排序是否发生交换，若未发生交换则序列有序，算法结束
        for(j=1;j<=i;++j){ //指针j扫描当前无序序列，用当前关键字与前一个关键字进行比较
            if(R[j-1]>R[j]){ //若前一个关键字大于后一个关键字则交换
                temp=R[j];
                R[j]=R[j-1];
                R[j-1]=temp;
                flag=1;
            }
        }
        if(flag=0)
            return;
    }
}

时间复杂度分析：

• 最坏情况：待排序列逆序，基本操作总的执行次数为n(n-1)/2，时间复杂度为O(n^2^)
• 最好情况：待排序列有序，内层循环不执行，时间复杂度为O(n)
• 平均情况：时间复杂度为O(n^2^)

空间复杂度：辅助数组仅有temp一个，空间复杂度为O(1)

2.2 快速排序

一趟快速排序的过程实际就是对无序序列进行一次划分的过程，划分后比枢轴小的关键字都在枢轴左边，比枢轴大的关键字都在枢轴右边。每趟快速排序结束后都会有一个关键字到达最终位置。

void QuickSort(int R[],int low,int high){ //对数组R从R[low]到R[high]的关键字排序
    int temp;
    int i=low,j=high;
    if(low<high){ //递归出口：若子序列长度大于1进行递归，否则退出递归
        temp=R[low]; //选择第一个关键字作为枢轴
        while(i<j){ //该循环完成对序列的一次划分/排序
            while(i<j && R[j]>=temp)
                j--; //从右往左找到小于temp的关键字
            if(i<j){
                R[i]=R[j]; //直接覆盖达到交换位置的目的
                i++;
            }
            while(i<j && R[j]<temp)
                i++; //从左往右找大于temp的关键字
            if(i<j){
                R[j]=R[i];
                j--;
            }
        }
        R[i]=temp; // 枢轴元素落入最终位置
        QuickSort(R,low,i-1); //枢轴元素左边进行快速排序
        QuickSort(R,i+1,high); //枢轴元素右边进行快速排序
    }
}

时间复杂度分析（快速排序的排序趟数与初始序列有关，待排序列越无序算法效率越高，待排序列越有序算法效率越低）：

• 最好情况：O(nlogn)
• 最坏情况：O(n^2^)。当初始序列有序或基本有序时，快速排序退化为冒泡排序
• 平均情况：O(nlogn)

3.选择类排序

3.1 简单选择排序

算法思想：从头到尾顺序扫描无序序列，选择最小的关键字与第一个关键字交换，接着从剩下的无序序列的关键字中继续这种选择和交换，最终使得序列有序

void SelectSort(int R[],int n){
    int i,j,k;
    int temp;
    for(i=0;i<n;i++){
        k=i; //变量k存储最值在数组中的下标
        for(j=i+1;j<n;j++){ //从无序序列中挑选最小的关键字
            if(R[k]>R[j])
                k=j;
        }
        //将选出的最小关键字与无序序列中第一个关键字进行交换（与有序序列始终无关）
        temp=R[i];
        R[i]=R[k];
        R[k]=temp;
    }
}

时间复杂度分析：简单选择排序的双层循环的执行次数和初始序列没有关系，基本操作执行总次数为n(n-1)/2，时间复杂度为O(n^2^)

空间复杂度分析：O(1)

简单选择排序有两个版本，数组使用交换版（不稳定），链表使用插入版（稳定）

3.2 堆排序

堆排序也称为快速选择排序，它在借助堆的性质可以很快选出序列中的最值。堆排序整个过程就是不断调整堆，使得不符合堆定义的完全二叉树变为符合堆定义的完全二叉树（下面代码假设完全二叉树从下标1开始存储，若从0开始存储则某些规则会有小变动）

//堆调整算法
void Sift(int R[],int low,int high){ //对数组low位置的结点在R[low]到R[high]范围内进行调整 -- 即对low结点进行一趟自上而下的堆调整
    int i=low,j=2*i; //若完全二叉树的下标从1开始存储，则此时R[2*i]是R[i]的左孩子（若下标从0开始存储则最后一个非叶结点为n/2-1，左孩子为2*i+1）
    int temp=R[i]; //暂存low结点的值
    while(j<=high){
        if(j<high && R[j]<R[j+1]) //若j=high说明只有左孩子没有右孩子（这种情况在完全二叉树中只有最后一个非叶结点会出现）
            j++; //若根的右孩子更大，则j指向右孩子，否则j仍然指向左孩子
        if(temp<R[j]){ //若R[j]的结点值大于双亲结点R[i]则交换两个结点
            R[i]=R[j];
            i=j; //修改i值以跟踪被调整的结点，直到一趟调整结束
            j=2*i; //假如j超出数组范围则循环结束
        }
        else 
            break; //若双亲结点大于孩子结点，则无需对该根结点进行调整
    }
    R[i]=temp; //low结点的值放入最终位置
}

//堆排序
void heapSort(int R[],int n){
    int i,temp;
    for(int i=n/2;i>=1;i--){ //利用数组R建大顶堆，n/2为最后一个非叶结点，自下而上建堆（注意堆调整是自上而下，建堆是自下而上）
        Sift(R,i,n)；
    }
    for(i=n;i>=2;i--){ //只需要进行n-1次的交换根结点的操作（最后一个根结点无需交换）即可构成有序序列R
        temp=R[i]; //将堆的根结点与堆的最后一个结点交换
        R[1]=R[i];
        R[i]=temp; 
        Sift(R,1,i-1); //堆调整，调整堆顶点选出剩余无序序列中最大值（快速选择）
    }
}

时间复杂度分析（适用于关键字个数非常多的情况下的排序）：

• 平均时间复杂度：对于函数Sift()即对每个结点调整的时间复杂度为O(logn)；对于函数heapSort，其基本操作总次数为两个并列for循环的基本操作次数之和，第一个for循环的基本操作次数为n/2*O(logn)，第二个for循环的基本操作次数为(n-1)*O(logn)，故最终时间复杂度为O(nlogn)
• 最坏时间复杂度：O(nlogn)

空间复杂度分析：算法所需辅助空间不随待排序列规模变化而变化，故空间复杂度为O(1)（是所有时间复杂度为O(nlogn)中空间复杂度最小的）

4.二路归并排序

归并排序可以看作是分治法的具体使用：先将整个序列分为两半，对每一半分别进行归并排序得到两个有序序列，将这两个有序序列归并为一个有序序列即可

//数组归并
void merge(int arr[],int low,int mid,int high){
    int i,j,k;
    int n1=mid-low+1; //low到mid的关键字个数（第一个数组的长度）
    int n2=high-mid; //第二个数组的长度
    int L[n1],R[n2]; //辅助数组用于暂存待归并的两个数组
    for(i=0;i<n1;i++){ //数组复制
        L[i]=arr[low+i];
    }
    for(j=0;j<n2;j++){
        R[j]=arr[mid+1+j];
    }
    i=0;
    j=0;
    k=low;
    while(i<n1 && j<n2){ //数组合并
        if(L[i]<R[j]) //选较小者进入arr数组，最终arr数组为非递增排序
            arr[k]=L[i]++; //将L[i]的值复制到arr[k]，同时i+1
        else
            arr[k]=R[j++];
        k++;
    }
    while(i<n1) //若L数组未排完则直接复制
        arr[k++]=L[i++];
    while(j<n2) //这两个循环只会执行其中一个
        arr[k++]=R[j++];
}

//归并排序
void mergeSort(int A[],int low,int high){
    if(low<high){
        int mid=(low+high)/2;
        megerSort(A,low,mid);
        mergeSort(A,mid+1,high);
        merge(A,low,mid,high); //将A中(low,mid)和(mid+1,high)两段有序序列归并为一段
    }
}

时间复杂度分析：选择merge内的归并操作为基本操作，其执行次数为要归并的两个子序列中关键字之和，整个归并排序总的基本操作执行次数为nlogn，时间复杂度为O(nlogn)。归并排序时间复杂度和初始序列无关，即最好、最坏以及平均时间复杂度均为O(nlogn)

空间复杂度分析：归并排序需要转存整个待排序列，故空间复杂度为O(n)

5.基数排序

基数排序的算法代码不做要求，假设n为待排序列中关键字的个数，d为待排关键字的位数，rd为关键字基的个数（桶的个数）。

时间复杂度分析（适用于关键字很多但关键字的基较小）：一趟“分配”和“收集”需要的时间为n+rd，整个排序需要d趟“分配”和“收集”，故时间复杂度为O(d(n+rd))

空间复杂度分析：每个桶实际都是一个队列，共rd个桶故空间复杂度为O(rd)

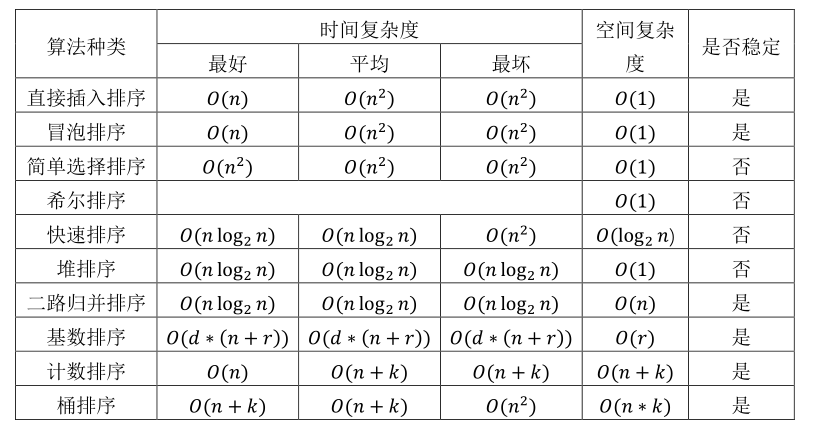
6.排序算法助记

6.1 时间复杂度与稳定性

下图是常见内部排序的时间复杂度与稳定性总结，需要记忆的是平均时间复杂度以及稳定性

“村里有两只动物，一只叫插帽龟（插入、冒泡、归并），一只叫做统计鸡（桶、计数、基数），它两做事情非常稳重（稳定）。

统计鸡喜欢做数学运算（加法和乘法，对应桶、计数、基数排序的平均时间复杂度）。某一天，插帽龟在选择帽子插的时候，恩姓长老慌了（选择、冒泡、插入，时间复杂度为n^2^），恩老大喊：“快点归还给堆”（快速、归并以及堆的时间复杂度为nlogn）。

”

最坏情况下，桶排序和快速排序的时间复杂度为O(n^2^)，其他与平均情况下相同（最好情况下的时间复杂度意义不大）

6.2 算法思想

下面这张表格帮助速记算法思想（仅仅针对我下面给出的代码，对其他书写风格的代码可能不适用）

算法	思想
插入排序（直接插入、折半、希尔）	前有序，后无序，无序逐个插有序（每趟无序第一个成为有序）
冒泡排序	前无序，后有序，无序换大到有序（每趟无序最后一个成为有序）
快速排序	j往左，i往右，j小i大换i,j，指针相遇填枢轴
简单选择排序	前有序，后无序，无序选小到有序（每趟无序第一个成为有序）
堆排序	前无序，后有序，无序选首到有序（每趟无序最后一个成为有序）
二路归并排序	从前往后两两归并（每个归并后的子序列分别内部有序）

6.3 常见结论

• 直接插入在“容易插”的情况下是O(n)，起泡“起得好”的情况下是O(n)，此处的“容易插和起得好”都指初始序列有序；快速排序反着来，“待排序列越无序算法效率越高，待排序列越有序算法效率越低”；
• 交换类（起泡、快速）和选择类（简单选择、堆）经过一趟排序，能够保证一个关键字到达最终位置
• 交换类排序，其排序趟数和原始序列相关
• 简单选择和折半插入，其关键字比较次数与原始序列无关（即比较次数一定）

八、查找

查找算法的基本操作是关键字的比较，而关键字的比较次数与待查找的关键字有关（即对同一个查找表中的不同关键字进行查找，关键字的比较次数一般不同）。因此一般将关键字的平均比较次数（也称为平均查找长度）作为衡量查找算法的指标。平均查找长度ASL的定义如下

其中n是查找表中记录的个数，pi是查找第i个记录的概率（一般取1/n），ci是找到第i个记录所需比较的次数，即查找长度。本章的算法没什么难度，难度主要就在ASL的分析上，针对每个查找算法给出详细的ASL计算步骤。

1.线性存储结构

1.1 顺序查找

//顺序表查找
int Search(int arr[],int n,int key){
    for(int i=0;i<n;i++){
        if(arr[i]==key)
            return i; //查找成功
    }
    return -1; //查找失败
}

//链表查找
LNode *Search(LNode *head,int key){
    LNode *p=head->next;
    while(p!=NULL){
        if(p->data==key){
            return p;
        }
        p=p->next;
    }
    return NULL;
}

1.2 折半查找

int Bsearch(int R[],int low,int high,int k){
    int mid;
    while(low<=high){
        mid=(low+high)/2;
        if(R[mid]==k)
            return mid;
        else if(R[mid]>k)
            high=mid-1;
        else
            low=mid+1;
    }
    return -1;
}

2.排序二叉树

2.1 查找

二叉树的查找算法思想与折半查找非常类似，直接看代码就可以理解，需要注意的是如果最后指向空指针域则表示查找失败。

非递归实现如下

BTNode *BSTSearch(BTNode *p,int key){
    while(p!=NULL){
        if(key==p->key)
            return p;
        else if(key<p->key)
            p=p->lchild;
        else
            p=p->right;
    }
    return NULL;
}

递归实现如下

BTNode *BSTSearch(BTNode *p,int key){
    if(p==NULL)
        return NULL;
    else{
        if(p->key==key)
            return p;
        else if(key<p->key)
            return BSTSearch(p->lchild,key);
        else
            return BSTSearch(p->rchild,key);
    }
}

2.2 插入

二叉排序树的本质就是一个查找表，因此插入一个关键字首先需要找到插入位置，对于一个不存在于二叉排序树中的关键字，其查找不成功的位置就是该关键字的插入位置（插入已有的关键字视为违规操作）。代码方面只需要对查找操作修改，来到空指针域时插入即可。

int BSTInsert(BTNode *&p,int key){
    if(p==NULL){ //p指向空指针域表示找到插入位置
        p=(BTNode *)malloc(sizeof(BTNode));
        p->lchild=p->rchild=NULL; //叶子结点没有孩子结点
        p->key=key;
        return 1;
    }
    else{
        if(key==p->key)
            return 0; //认为插入相同值为违法操作
        else if(key<p->key)
            return BTSInsert(p->lchild,key);
        else
            return BTSInsert(p->rchild,key);
    }
}

2.3 构造

借助上述插入操作，只需要建立一棵空树，然后将关键字逐个插入到空树中即可构建一棵二叉排序树

void CreateBST(BTNode *&bt,int key[],int n){
    bt=NULL;
    for(int i=0;i<n;i++)
        BSTInsert(bt,key[i]);
}